NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 31/01/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Types de TRIANGLES			Glossaire Triangle
INDEX TRIANGLE	Général	Triangle isocèle
	Types	Débutant	Isocèle de 45° au sommet
	Quelconque	Développements	Isocèle – Intersections
	Rectangle	Propriétés	Isocèle – Bissection
	Équilatéral	Résolution	Isocèle – Construction
		Isocèle Rectangle	Isocèle – 20 80 80
		Sommaire de cette page >>> Caractérisation du triangle isocèle >>> Principales relations métriques >>> Médianes

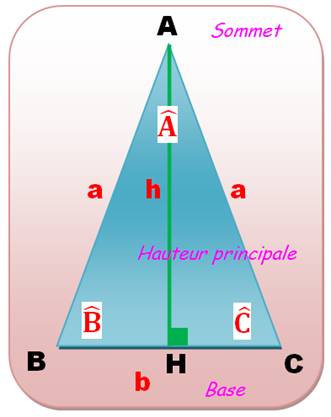
TRIANGLE ISOCÈLE

Fiche résumant les propriétés

Relations entre la longueur des côtés et la mesure des angles.

Autres propriétés et relations métriques.

Caractérisation du triangle isocèle
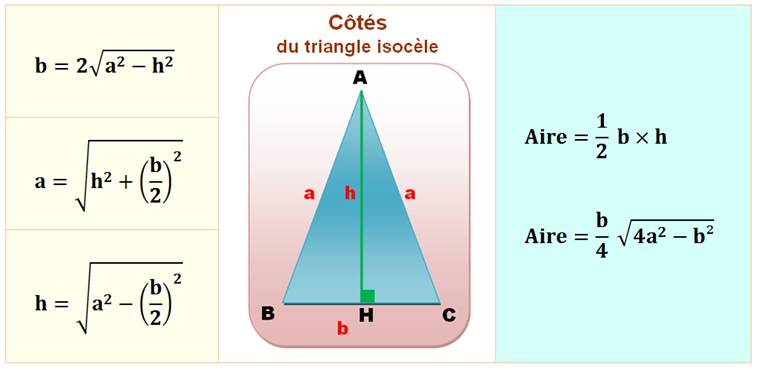
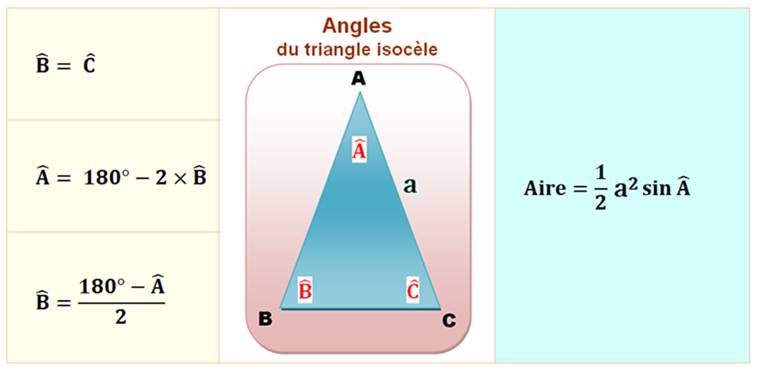
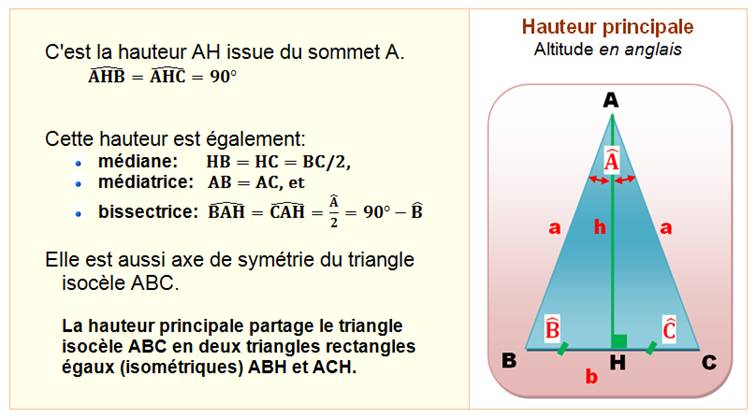
Côtés Un triangle est isocèle si au moins deux de ses côtés ont même longueur. AB = AC Th: Si dans un triangle deux côtés ont même longueur, les angles opposés sont égaux. Angles Un triangle est isocèle si au moins deux de ses angles sont égaux. Th: Si dans un triangle deux angles sont égaux, les côtés opposés ont même longueur. Symétrie Un triangle est isocèle s'il a au moins un axe de symétrie. La droite portée par AH est un axe de symétrie du triangle ABC. Un triangle est isocèle si une des hauteurs au moins partage ce triangle en deux triangles égaux (isométriques). Médianes et autres céviennes Un triangle est isocèle si au moins deux de ses médianes ont même longueur. BM = CN >>> Propriétés vraies également pour les hauteurs et les bissectrices.	Si le triangle est isocèle: AB = AC = a BH = HC

Relations principales: côtés, angles et hauteur principale
Angles Longueurs Hauteur principale

Médianes
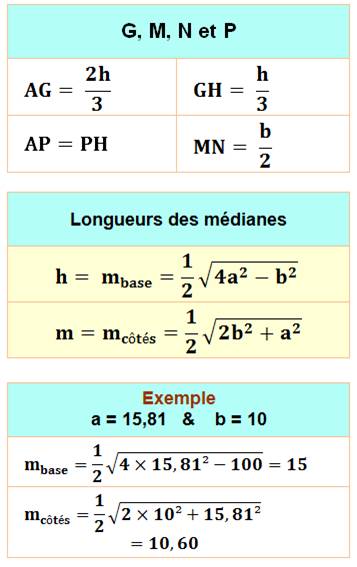
Voir Longueur des médianes			Les médianes se coupent en G, le centre de gravité du triangle.
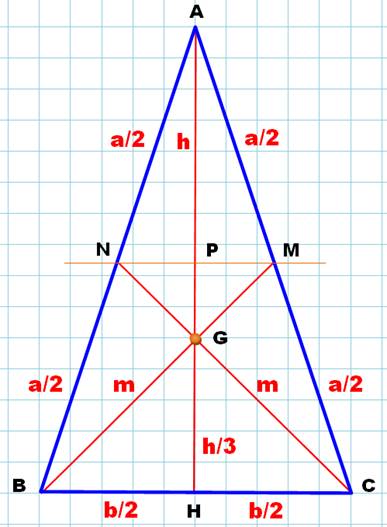
Les médianes BM et CN sont de même longueur. Cela parait évident du fait de la symétrie introduite par la droite AH.	Démonstration Sachant que AB = AC et que M et N sont les milieux de ces segments, démontrez que BM = CN. Dans les triangles AMB et ANC: L'angle A est commun; AB = AC; et AM = AN. Ces deux triangles sont égaux (isométriques). La troisième côté de l'un est de même longueur que le troisième côté de l'autre: BM = CN
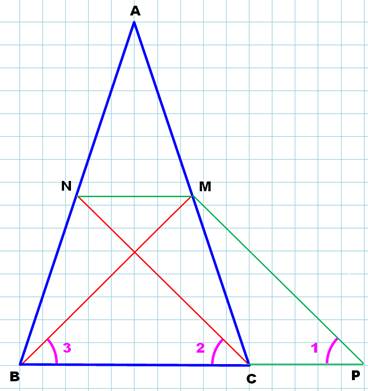
Si deux médianes sont de même longueur, le triangle est isocèle. Démonstration Un triangle quelconque avec AN = NB et AM = MC; BM = CN Démontrez que ce triangle est isocèle. On se sert de la construction indiquée: MP parallèle à NC P intesection de MP avc BC L'idée consiste à montrer que le triangle MBP est isocèle. Les angles à la base (1 et 3) sont égaux et aussi égaux à 2.
Les points M et N sont les milieux de AB et de AC. NC est parallèle à MP.		MN et parallèle à BC. Le quadrilatère NMPC est un parallélogramme. Ses côtés NC et MP sont de même longueur.
Les médianes sont de même longueur.		NC = MP = MB Le triangle MBP est isocèle. Angle 1 = Angle 3
NC et MP sont parallèles.		Angle 1 = Angle 3 = Angle 2
Triangles BCM et BCN.		Même base BC Angle 3 = angle 2 BM = CN Ces deux triangles sont égaux.
Les côtés sont égaux deux à deux.		CM = BN 2CM = 2BN AB = AC

Suite	Partage du carré en triangles isocèles Résolution du triangle isocèle Triangle – Index Triangle isocèle – Bissection Triangle isocèle – Intersections Triangle isocèle de 45° au sommet Types de triangles
Voir	Allumettes et quatre triangles isocèles Égalités des triangles Jeux Médianes Platon et sa vision des éléments Polygones Probabilité d'obtenir un triangle obtusangle Quadrupler le triangle Résolution du triangle quelconque Triangle de Pythagore
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/TrgIsocP.htm