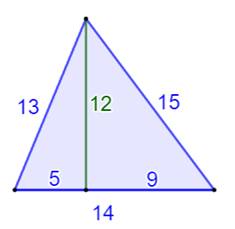
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Résolution du TRIANGLE (13, 14, 15) Triangle rationnel ou héronien Triangle singulier, dit héronien, avec ses côtés en nombres entiers croissants dont
la hauteur (h = 12) et l'aire
(A = 84) sont aussi des nombres entiers. Triangle connu par les Grecs anciens, les Hindous
ou encore les Arabes. On se demande si tous ces mathématiciens ont eu accès à
la même source ou si ce sont des découvertes indépendantes. Exemple pour eux de la démonstration de la relation de Héron. |
Anglais: solving triangles
|
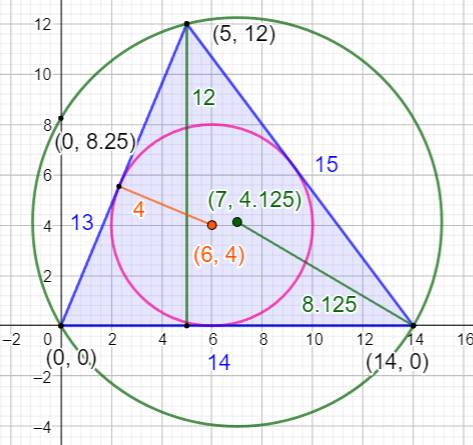
Triangle {13, 14, 15} Ce triangle présente
quelques autres longueurs en nombres entiers ou en nombres rationnels simples. Notamment le rayon du centre
du cercle inscrit vaut 4. Ses coordonnées sont (6,4) Valeurs principales
|
Valeurs détaillées
|
|
Voir Énigme
avec le triangle {13, 14, 15}
|
|
||
|
Présentation Triangle
qui a tous ses angles aigus (acutangle)
et dont les mesures des côtés (13, 14
et 15) sont des nombres entiers consécutifs. Non
seulement une des hauteurs est également un nombre entier, mais ce nombre
(12) aussi consécutif avec les côtés. La
découpe de la hauteur sur le côté est également en nombres entiers (9 et 5). L'aire
est un nombre entier (84). Périmètre: 13 + 14 + 15 = 3 x 14 = 42 |
|
|
|
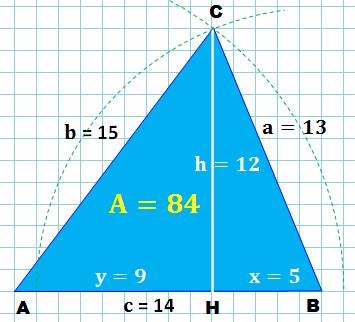
Calcul général (Méthode d'Al-Khwarizmi en 820) Dans les deux
triangles rectangles définis par la hauteur et avec le théorème de Pythagore. |
h² = b² – (c – x)² = b² – c² + 2cx –x² h² = a² – x² b² – c² + 2cx = a² x = (a² – b² + c²) / 2c |
|
|
Application au triangle (13, 15,
14) En reprenant les
formules ci-dessus. Le plus petit triangle acutangle quelconque avec
une aire rationnelle. |
x = (13² – 15² + 14²) /
(2x14) = 140 / 28 = 5 h² = 13² – 5² = 144 h = 12 A = ½ x 12 x 14 = 84 |
|
Voir Suite du calcul et relation de Héron
|
|
||
|
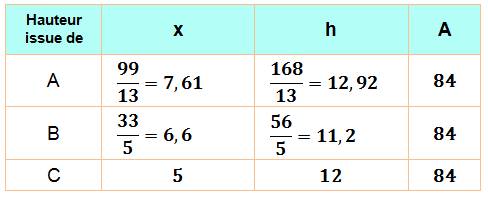
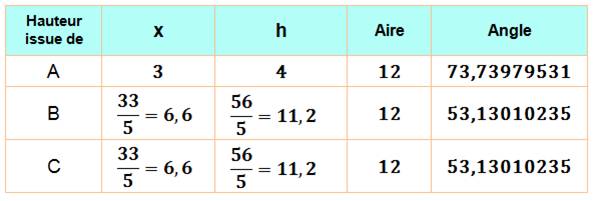
Hauteur Pour
chaque hauteur issue des sommets An B ou C, on donne la découpe x de la
hauteur sur le côté opposé, la longueur de la hauteur et l'aire calculée à
partir de cette hauteur (trois fois la même valeur, heureusement) |
|
|
|
Angles Avec la formule des cosinus, on calcule la valeur des
angles. Connaissant
h, il est également facile d'utiliser la trigonométrie
classique avec tan A = 12 / 9 => A = 53, 130 … |
|
|
|
Autres mesures |
Médianes:
12,971; 12,166; 11,236 Rayon du
cercle inscrit: 4 Rayon du
cercle circonscrit: 8,125 Coordonnées
A(0; 0), B(15; 0), C(6,6; 11,2) Centre de
gravité: (7,2; 3,733) |
|
|
Nombres consécutifs pour les côté et
hauteur rationnelle |
En 1722,
Nakne Genkei a trouvé: (3, 4, 5), (13, 14, 15),
(51, 52, 53) et (193, 194, 195). |
|
Suite |
|
|
Voir |
|
|
E. R. Suryanarayan
|
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/T131415.htm
|
