|
|||||||||||||||||||||||||||||||||||||||||||||
Anglais: Matchstick
construction
![]()
|
Transformer une figure en une autre en déplaçant
des allumettes Les possibilités sont
infinies. Certains magazines de jeux vous en proposent. Sur cette page, les
plus classiques. |
|
|
|
|
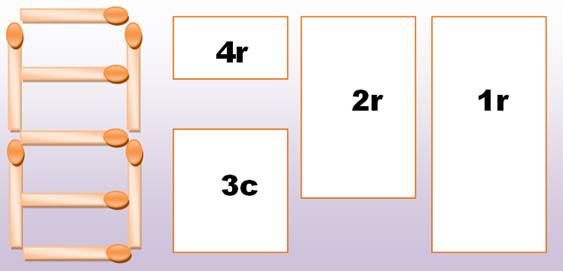
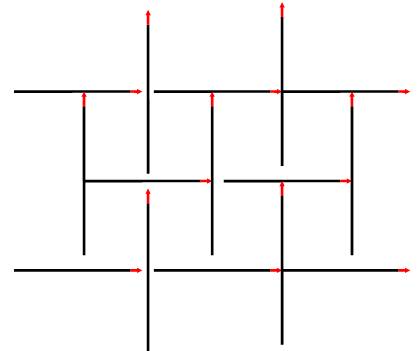
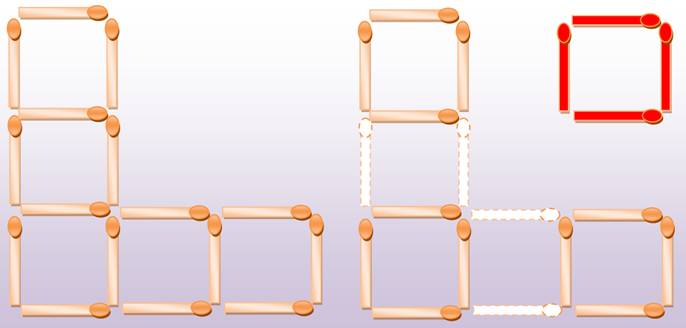
Énigme très
simple: faire dix rectangles avec neuf allumettes.
Dénombrement
des rectangles dans cette figure avec neuf allumettes. 10 rectangles
dont 3 carrés. 10 = 4 + 3 + 2 + 1 est un nombre triangulaire. Avec quatre
allumettes de plus, on aurait: 6 + 5 + 4 + 3 + 2 + 1 = 6 x 7 / 2 = 21 rectangles. |
|
|
|
|
|
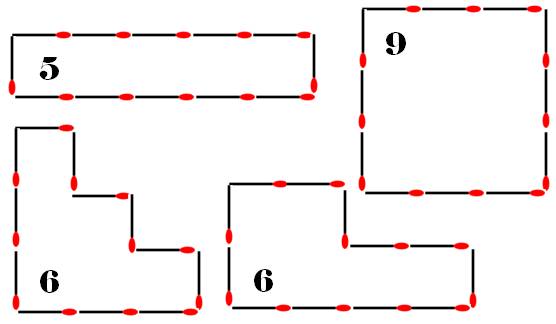
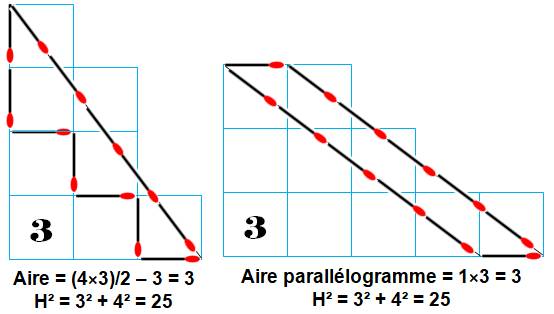
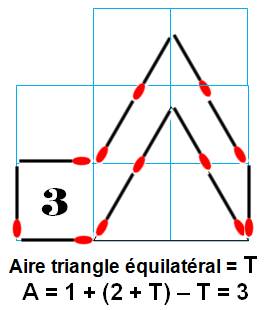
Avec douze
allumettes, on sait faire des polygones d'aire: 9, 6, 5. Est-il possible
de descendre à une aire de 3 ?
Plus original:
|
|
|
|
|
|
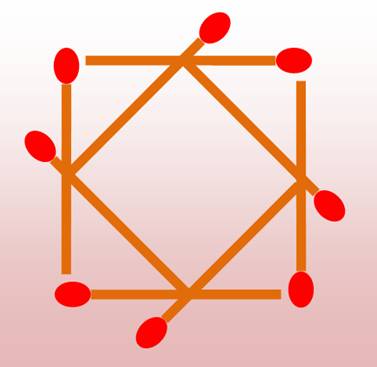
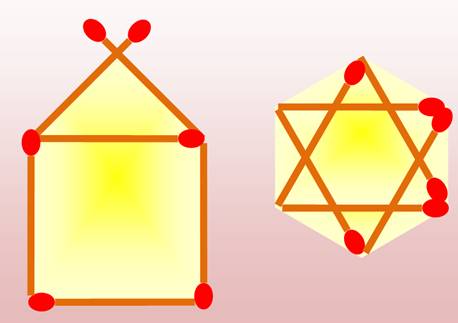
Avec huit allumettes formez deux carrés et
quatre triangles. Quatre
allumettes dessinent un carré. Les
quatre autres relient les milieux des côtés. Évidemment elles débordent le carré.
Elle forment un deuxième carré.
La
figure montre effectivement deux carrés
et quatre triangles
isocèles rectangles. Dans
le même style de figure Transformer
l'enveloppe en étoile de David
(6 triangles isocèles)
|
|
|
|
|
|
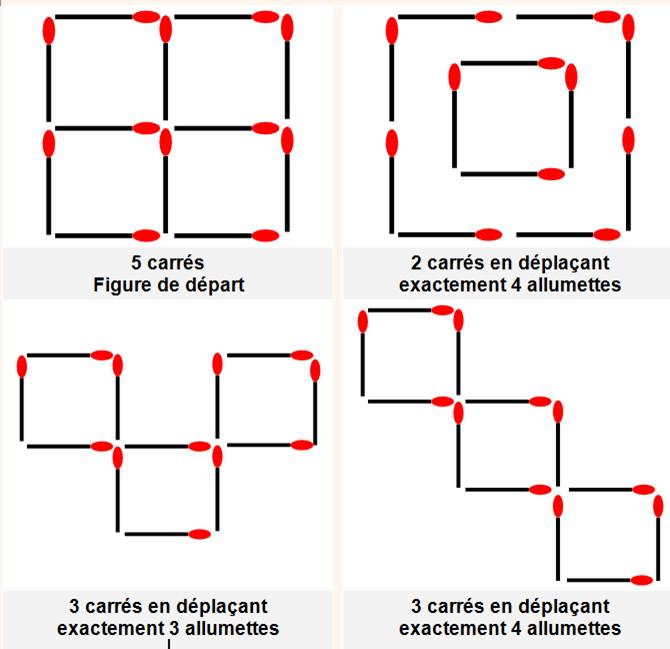
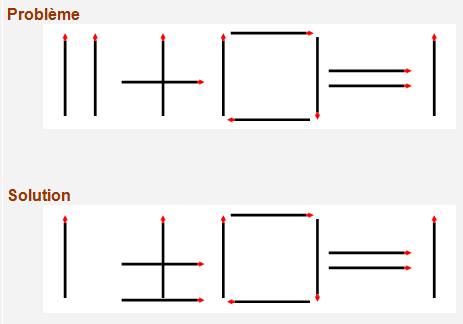
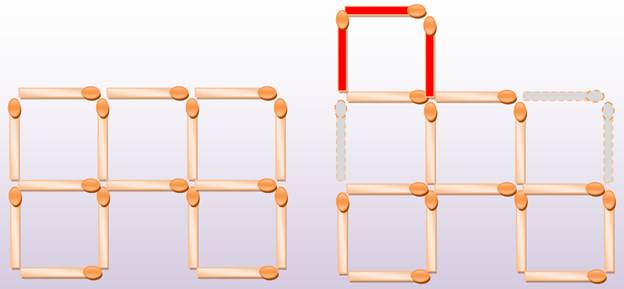
Avec
la figure de gauche comportant cinq carrés, déplacez trois
allumettes pour obtenir exactement quatre
carrés (figure de droite).
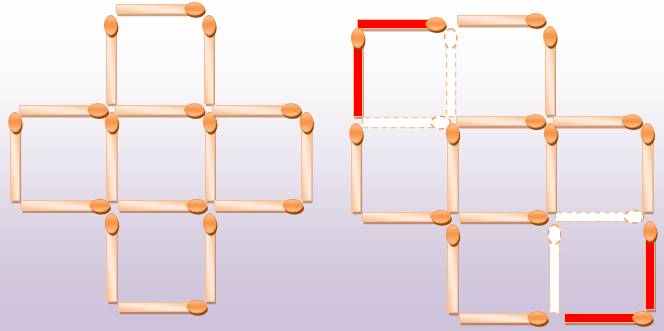
Avec
la figure de gauche comportant cinq carrés, déplacez quatre
allumettes pour obtenir exactement trois
carrés (figure de droite).
Avec
la figure de gauche comportant cinq carrés, déplacez quatre
allumettes pour obtenir exactement quatre
carrés (figure de droite).
|
|
|
|
||
|
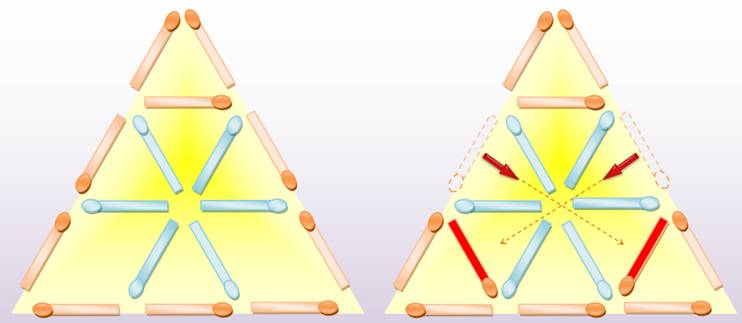
À gauche: 5 petits triangles. |
À droite: en déplaçant deux allumettes: 7 petits triangles. |
|
|
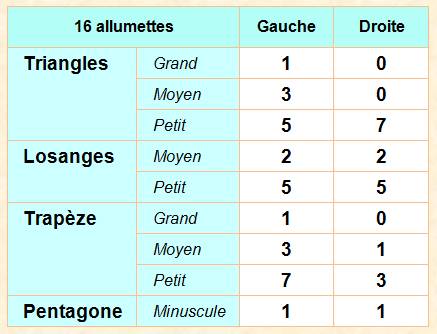
Dénombrement
Le
pentagone est au centre des allumettes bleues en étoile. |
||
Voir Triangle / Losange
/ Trapèze
/ Pentagone
/ Dénombrement
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()