Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 01/02/2024 M'écrire Brèves de Maths

INDEX Triangle Géométrie	Triangles isocèles
	Débutant	Isocèle Rectangle	45° au sommet	Construction
	Développements	Résolution	Intersections	20 80 80
	Propriétés	Sept triangles	Bissection	36 72 72

Triangle ISOCÈLE RECTANGLE Triangle rectangle dont deux côtés sont égaux. Ses deux autres angles valent 45°. Le carré coupé en deux par une de ses diagonales produit deux triangles isocèles rectangles. Avec ses deux diagonales, il y en a quatre.
	Sommaire de cette page >>> Approche >>> Propriétés >>> Cercles inscrits	Débutants Triangle Glossaire Triangle

Anglais: isosceles right triangles

Approche		haut
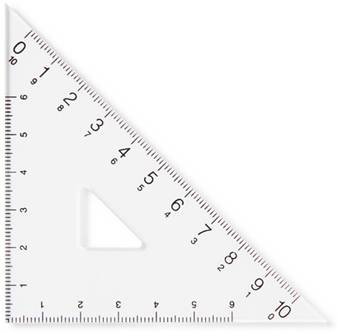
Équerre d'écolier Une des équerres utilisées par les écoliers est en forme de triangle isocèle rectangle: Angles 45° - 45° - 90°. Côtés de l'angle droit égaux (isométriques). Définition Un triangle isocèle est rectangle si son angle au sommet est droit. Les angles à la base valent chacun 45°. En effet: 45°+ + 45° + 90° = 180°, somme des angles dans un triangle. Propriétés Deux triangles isocèles-rectangles juxtaposés par leur hypoténuse forment un carré. Deux triangles isocèles-rectangles tête-bêche forment un quadrilatère dont les diagonales sont perpendiculaires (sommet-droit en commun).	Exemple d'équerre d'écolier

Voir Exercice d'application / Tangram / Carré max. en triangle unitaire

Propriétés		haut
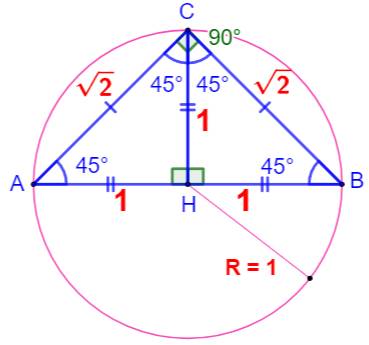
Ce qu'il faut savoir Avec sa hauteur principale, le triangle isocèle rectangle est divisé en triangles du même type, donc semblables. Si la base Ab mesure 2, cette hauteur CH mesurera 1 et ses côtés AC et BC mesureront racine de 2. Si le côté AC mesure 1, alors toutes les autres dimensions seront divisées par racine de 2. Ainsi, la base AB mesurera 2/√2 = √2. Le triangle ABC présente un angle droit en C, il est inscrit dans un cercle dont le segment AB est un diamètre et le point H, le centre. Aire: ½ x 1 x 2 = 1 Si a = AC et c = AB alors: A = a² / 2 = c² / 4. Périmètre: 2 + 2√2 Si a = AC et C = AB alors: P = a(2 + 2√2) = b(1 + √2)	Mensurations principales
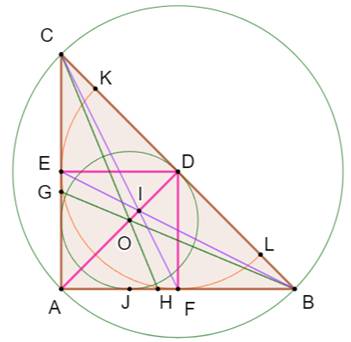
Points singuliers Le point A est l'orthocentre (hauteurs). Le point D est le centre du cercle circonscrit (médiatrices). Le point D est aussi le centre du demi-cercle KEFL, tangent aux deux côtés de l'angle droit.	Le point O est le centre du cercle inscrit (bissectrices en vert). Le point I est le centre de gravité (médianes en mauve)

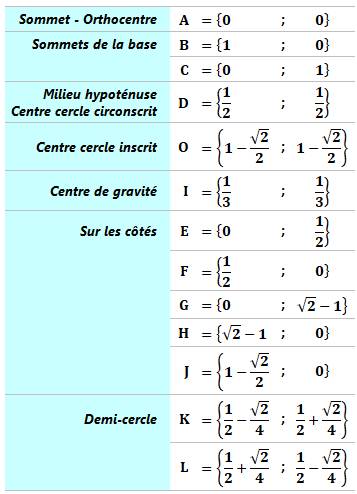
Coordonnées des points singuliers Repère d'origine A et d'axes sur AB et AC.

Notations

Voir Droites et points dans le triangle

Bilan

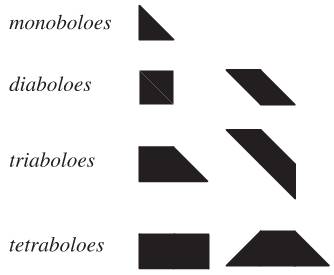
Les polyformes réalisées avec des triangles isocèles rectangles son appelées polyabolos ou polytans ou super tangrams. Tableau complet >>> La quantité de polyabolos formés de n triangles est: 1, 3, 4, 14, 30, 107, 318, 1116, 3671, … OEIS A006074

Voir Polyominos

Demi-cercles inscrits dans le triangle isocèle rectangle		haut
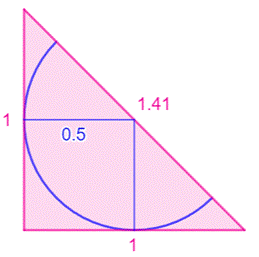
Demi-cercle sur l'hypoténuse Un triangle isocèle rectangle de côté unité. Un demi-cercle dont le diamètre est sur l'hypoténuse et qui est tangent aux deux côtés de l'angle droit. Par symétrie, le centre sur cercle est au milieu de l'hypoténuse, laquelle mesure: Deux rayons perpendiculaires aux côtés (bleus) forment deux petits triangles isocèles rectangles. Application du théorème de Pythagore dans l'un d'eux:	Dans ce cas, le rayon est égal à:
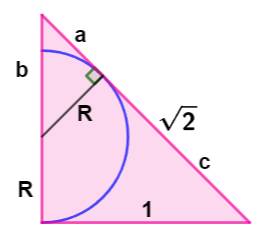
Demi-cercle sur un des côtés Un triangle isocèle rectangle de côté unité. Un demi-cercle dont le diamètre, issu du sommet de l'angle droit est sur l'un des côtés et est tangent à l'hypoténuse. Le rayon issu du point de tangence est perpendiculaire à la tangente, formant un petit triangle rectangle. Les deux segments de tangente issus du même point sont égaux (isométriques) et valent 1. L'hypoténuse valant racine de 2, les deux côtés de l'angle droit mesurent 1. Application du théorème de Pythagore dans le triangle rectangle:	Dans ce cas, le rayon est égal à:

Voir Exercice d'application / Tangram / Carré max. en triangle unitaire

Haut de page

Retour	Triangle isocèle Voir Haut de page
Suite	Triangle isocèle rectangle et bissectrice Triangles rectangles entiers – de Pythagore Triangles rectangles particuliers Triangle équilatéral
Voir	Losange Puzzle chinois Rectangle Triangle – Index Types de triangles
Sites	Triangle isocèle rectangle – Wikipédia Isosceles Right Triangle – Wolfram MathWorld Polyoboloes – The Poly Pages
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/TrgIsoRe.htm