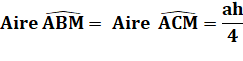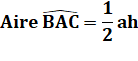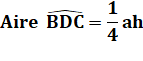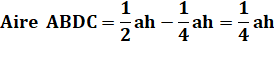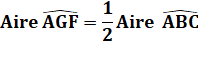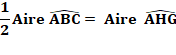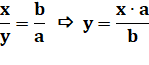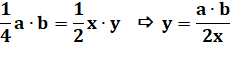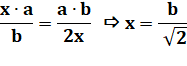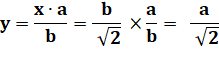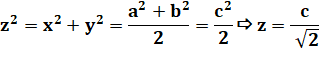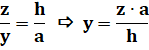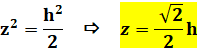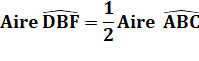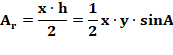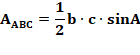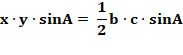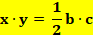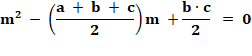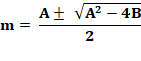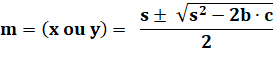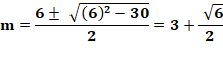Découpe de même aire

Édition du: 18/06/2021

INDEX Types de triangles Triangle	Triangles – Curiosités
	Point Milieu	Droites et points	Pappus	Point et triangles
	Aire = Aire	Quantité de triangles	Torricelli	Triangles et triangles
	Médianes	Quatre triangles	Heilbron	Carrés triangles
	Résolution	Représentation	Brocard	Cercles et triangles

Partage du triangle

en parts égales (de même aire)

Comment partager le triangle en deux (ou plus) figures de même aire en dessinant simplement une droite avec ou sans contrainte ?

Comment y associer une égalité de périmètre ? >>>

Où l'on remarquera que la droite de découpe ne passe pas forcément par le centre de gravité >>>

Profitez d'une astuce de résolution des équations avec somme et produit >>>

Sommaire de cette page

>>> Triangle quelconque: avec la médiane

>>> Triangles en deux parts égales

>>> Triangle quelconque: avec une parallèle – coupé en 2 parts

>>> Triangle quelconque: avec une parallèle – coupé en k parts

>>> Triangle rectangle – Construction

>>> Triangle rectangle – Justification

>>> Triangle isocèle – Calcul

>>> Triangle Quelconque – Selon une droite (ou un point)

>>> Triangle Quelconque – Aire et périmètre

Débutants

Triangles

Glossaire

Triangles

Remarque

Quelle que soit la quantité de droites qui sectionnent le triangle, il y aura toujours au moins un triangle qui subsistera.

Triangle quelconque: avec la médiane

haut

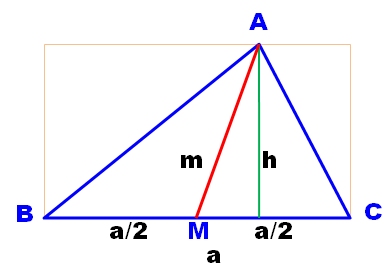
Le moyen le plus simple pour partager un triangle en deux triangles de même aire consiste à tracer une médiane.

Un triangle quelconque ABC et la médiane AM.

La médiane partage le triangle en deux triangles ABM et ACM de même aire:

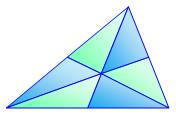
Rappel: les trois médianes partagent le triangle en six triangles de même aire.

Triangle en deux parts égales

haut

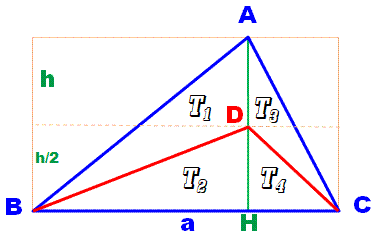
Comment simplement partager un triangle en deux parties de même aire ? Ici, avec deux traits.

Un triangle quelconque ABC et la hauteur AH.

Le point D est le milieu de cette hauteur.

T₁ = T₂; T₃ = T₄; T₁ + T₃ = T₂ + T₄

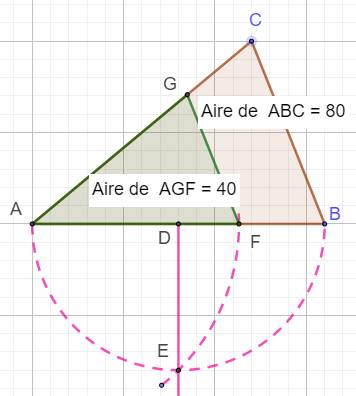
Triangle quelconque: avec une parallèle		haut
Partage en deux parts égales Il s'agit de partager un triangle en deux parties de même aire avec le tracé d'une parallèle à un des côtés. Un triangle quelconque ABC On souhaite construire le triangle AFG tel que: Construction Demi-cercle AB qui coupe la médiatrice de AB en E. Arc de cercle de centre A et de rayon AE qui coupe AB en F. Parallèle en F à BC qui coupe AC en G. FG est la droite de partage du triangle ABC en deux parts de même aire. Voir la justification avec le triangle rectangle, sachant que tout triangle est décomposable en deux triangles rectangles via le tracé d'une hauteur..
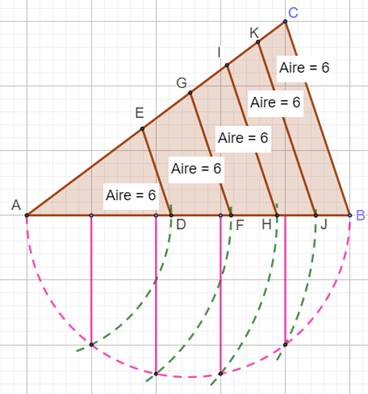
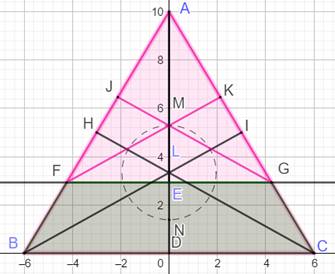
Partage en k parts égales La méthode s'applique à k parts de même aire. Construction pour k = 5 Diviser AB en cinq segments égaux. Tracer les perpendiculaires (roses) à AB à partir des quatre points. Elles interceptent le demi-cercle en quatre points. Tracer les arcs de cercle à partir de A et qui passent par ces quatre points (verts). Ils coupent AB en quatre points. À partir de ces quatre points, tracer les parallèles au côté BC. Elles partagent le triangle ABC en cinq polygones (un triangle et quatre trapèzes) de même aire. Aire du triangle ABC = 10 x 6 / 2 = 30. Aire de chaque polygone: 30 / 5 = 6.

Voir Cas général

Triangle rectangle – Construction

haut

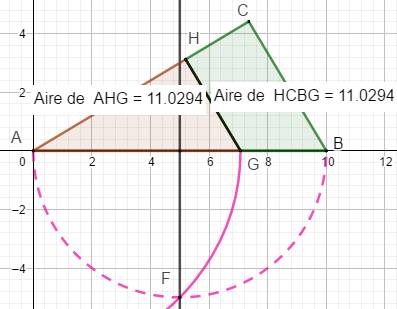
Comment partager le triangle rectangle en deux surfaces égales avec une droite parallèle à un des côtés de l'angle droit ?

Un triangle rectangle ABC.

On souhaite:

Construction (idem celle-ci-dessus)

Demi-cercle AB qui coupe la médiatrice de AB en F

Arc de cercle de centre A et de rayon AF qui coupe AB en G.

Parallèle en G à BC qui coupe AC en H

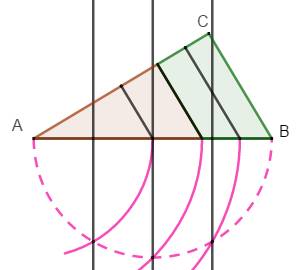
HG est la droite de partage en deux parts de même aire.

Cette construction pour 2 est valable pour un partage en k parties de même surface. Divisez alors AB en k segments égaux.

Exemple avec k = 4 =>

Triangle rectangle – Justification

haut

La construction nous donne

Les aires étant dans un rapport 2, les dimensions sont dans un rapport racine de 2.

En effet

z = AG = AF et z² = (c/2)² + (c/2)² = c²/2

Triangle isocèle – Calcul (à titre d'exercice et d'observation sur le centre de gravité)		haut
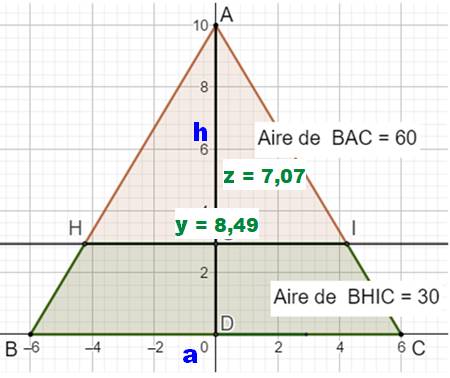
Comment partager le triangle isocèle en deux surfaces égales avec une droite parallèle à la base ? Un triangle isocèle ABC. Longueur de la base = a et hauteur = h Le triangle isocèle AHI. Longueur de la base = y et hauteur = z On souhaite: Les valeurs numériques résultent du calcul qui suit.
Proportionnalité des triangles isocèles
Aire du grand = 2 x aire du petit
Calculs
Application numérique

Centre de gravité

Notez bien que la droite passant par le point E partage le triangle en deux parts égales, mais non-symétriques.

Le point E n'est pas le centre de gravité.

Celui-ci (L) est à l'intersection des trois médianes.

Si M est le centre de gravité du triangle rose, pour assurer l'équilibre, le centre de gravité du trapèze gris est le point N, symétrique de M par rapport à L.

Image de la balance: L est le point d'appui et M et N les plateaux supportant les mêmes masses (mêmes aires donc mêmes quantités de matière, si homogène). Il y a donc équilibre.

Triangle Quelconque – À partir d'un point			haut
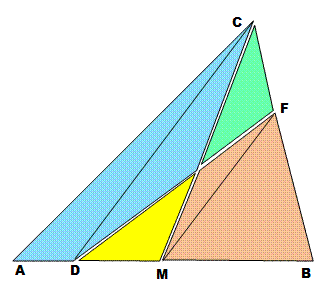
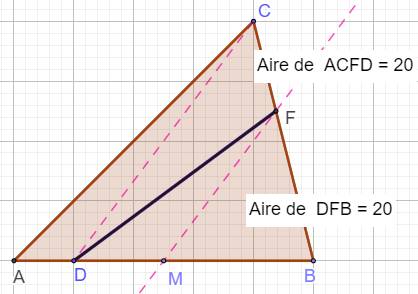
Partage en deux parts égales à partir d'un point du triangle Il s'agit de partager un triangle en deux parties de même aire avec le tracé d'une droite issue d'un point D du périmètre du triangle. Un triangle quelconque ABC. On souhaite construire le triangle DBF tel que: Construction Segment CB. Milieu M de AB et parallèle en B à CD. La droite DF partage le triangle en deux polygones de même aire.
Justification Le quadrilatère DCFM est un trapèze et ses triangles latéraux ont la même aire: Vert = Jaune Les deux triangles CAM et CBM, avec la même hauteur et une base égale (AM = MB) ont la même aire. Bleu + Jaune = Vert + Marron En inversant Vert et Jaune Bleu + Vert = Jaune + Marron La construction revient à tracer la médiane et à basculer autant de surface d'un côté et de l'autre.

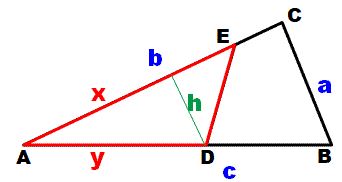
Triangle Quelconque – Aire et périmètre		haut
Partage en deux parts égales avec même périmètre Il s'agit de partager le triangle ABC en deux parties de même aire en donnant le même périmètre aux deux polygones Calculs
Même périmètre (ED étant commun)	x + y = (b – x) + (c – y) + a 2(x + y) = a + b + c
Aire triangle rouge	Ar = 1/2 xh = 1/2 x y sin A
Aire du triangle ABC
L'une égale moitié de l'autre
Remarque à ce stade: la contrainte sur le périmètre engendre une relation sur la somme des distances. la contrainte sur l'aire engendre une relation sur le produit des distances. Il s'agit de résoudre deux équations avec somme et produit.
Introduction d'un variable intermédiaire (astuce !): m = x ou y	(m – x ) (m – y) = 0 m² - (x+ y)m + xy ) = 0
Avec les valeurs de la somme et du produit équation du second degré à résoudre.	m² - Am + B = 0
Racines
Finalement: valeur de x ou de y. Avec s = (a + b+ c ) / 2 (demi-périmètre).
Exemple avec le triangle (3, 4, 5) Seul choix qui marche: a = 4, b = 5 et c = 3	x = 4,225… et y = 1,775…

Calculs selon ceux développés par Aous Manshad

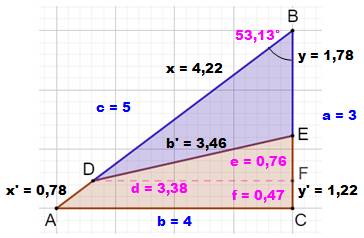
Le triangle (3, 4, 5) coupé en deux parts égales et avec le même périmètre

Périmètres

BDE: 4,22 + 3,46 + 1,78 = 9,46

DACE: 0,78 + 4 + 1,22 + 3,46 = 9,46

Aires (avec angle en B)

sinus (53,13°) = 4 / 5 = 0,8

Aire BDE: 4,22 x 1,78 x 0,8 / 2 = 3

Aire ABC = 3 x 4 / 2 = 6

Aire DACE: 6 – 3 = 3

Aires (avec dimensions mesurées)

Aire BDE: 3,38 x 1,78 / 2 = 3

Aire DACE: 0,47(4 + 3,38)/2 + 3,38x.76/2 = 3

Haut de page

Retour	Triangles et droites de partage Constructions géométriques - Index
Suite	Bissection du triangle Illustration en 3D du centre de gravité d'un triangle Quatre triangles Triangles et carrés Triangle – Index
Voir	Cercle Application somme-produit au calcul d'une longueur de corde dans un cercle DicoMot Losange et son cercle inscrit Médianes – Glossaire
Sites	Trisections the areas of a triangles – Gayle Gilbert Cutting a triangle into two pieces of equal area and equal perimeter – Aous Manshad – 2009 Cutting Triangle in Two by a Line through a Point – Cut-The-Knot – Montre comment partager en deux avec une droite passant par un point externe.
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/AireAire.htm