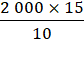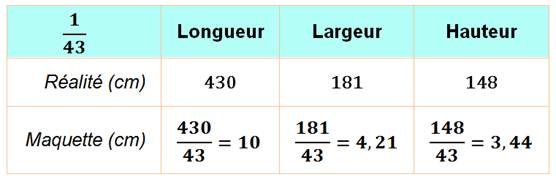|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
PROPORTIONS & RÈGLE DE TROIS Pratique
et pièges! Comment
raisonner pour s'y retrouver à coup sûr ? Trois
nombres à la fête: la règle de trois, la quatrième
proportionnelle et le pourcentage.
Notions
voisines: échelle, agrandissement, réduction, proportions |
Voir Nombre 100

Pour
compléter voir Proportionnalité et règle de
trois – Glossaire
Un classique de l'humour anglais: la règle de trois appliquée
aux verbes irréguliers
|
Dommage
la réponse est fausse! Le participe passé est flowed. |
Voir Anglais
/ To grow = croître, pousser et to flow
= couler, circuler
![]()
RÈGLE DE TROIS telle que présentée dans un
manuel pratique de 1933
|
Quand deux
grandeurs sont telles que, si l'une devient un certain nombre de fois plus
grande ou plus petite, l'autre devienne ce même nombre de fois plus grande ou
plus petite, ces deux grandeurs sont dites proportionnelles. Exemple: 10 hectolitres de vin
coûtent 2 000 Fr. On demande de trouver le prix de 15 hectolitres du même
vin. Les deux
grandeurs proportionnelles sont les hectolitres et les francs. Ce problème,
dont l'énoncé contient trois nombres, fait appel à la règle de trois. La solution
s'obtient par la méthode de la réduction à l'unité. 10 hl coûtent 2 000 Fr. 1 hl
coûte 10 fois moins ou 15 hl coûtent 15 fois plus ou |
|
|
|||||||
|
LE
PRODUIT EN CROIX
|
Égalité de fractions à trou
Produit en croix 2 . x = 1 . 48 x = 48 / 2 = 24 |
||||||
|
Connaissant ce
truc de la règle de trois (ou du produit en croix, c'est la même chose) nous
allons donner quelques exemples de calcul. Note: on adopte parfois le point pour la multiplication. Cela évite la
confusion entre le signe multiplier |
|
|
||||||||
|
Des tomates à 2 euros les 4 kg Combien valent 7 kg ? Le produit en croix donne 3,5 euros. En effet le kg
vaut 2 / 4 = 0,5 euros par kg. Et,
7 kg font: 7 |
X = 2 = 3,5
euros |
|||||||
|
20 personnes fabriquent 200 chaises en un
jour. Combien faut-il de personnes pour en fabriquer 300 dans la journée? |
X = 20 = 30
personnes |
|||||||
|
|
||||||||
|
15 hommes cueillent le verger en 28 jours.
Combien de temps pour 5 hommes seulement? Le produit en croix posé un peu rapidement
ne marche pas. Avec 5 hommes au lieu de 15, il est évident qu'il faudra
beaucoup plus de 28 jours. Compte tenu des nombres utilisés, on peut même
remarquer le rapport 3 entre 5 et 15 et dire immédiatement qu'il faut 28 x 3
= 84 jours. Donc, la règle de trois, posée mécaniquement, donne n'importe
quoi.
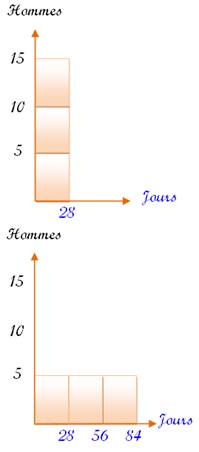
Faire un dessin: il est alors possible de
rendre compte de la situation. Et même de voir qu'il faut l'équipe de 5
hommes durant trois fois 28 jours. La surface colorée représente le travail
pour récolter tout le verger T = 28 jours 15 hommes Quel que soit le nombre de personnes le
travail total reste le même, y compris avec 5 hommes T = X jours
15 hommes font la
récolte complète en 28 jours; Dans le même temps, 5 hommes (le tiers) feront
le tiers du travail, soit un tiers de la récolte du verger. Pour faire la
récolte complète, il faudra trois fois plus de temps, soit 28 |
Produit en croix
X = 28 FAUX On sait
qu'il faut plus de 28 jours avec moins de personnes! Illustration
Bilan T = 28
jours T = X jours X = 28 |
|||||||
Règle
importante

|
|
||
|
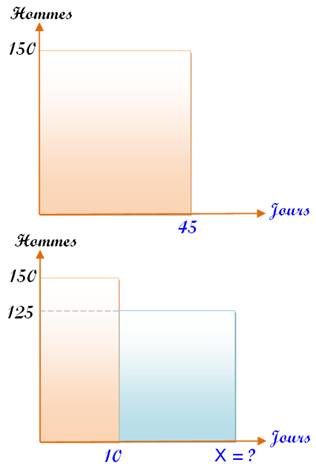
On dispose de provisions pour 150 hommes et
45 jours. Après 10 jours, 25 personnes débarquent. Combien de jours de mission encore possible ?
Le rectangle rose (dessin du
haut)
représente les provisions embarquées pour 45 jours et 150 hommes. Il y a du stock de provisions (P)
embarquées pour toute la mission. Ce stock servira finalement pour (dessin du
bas).
Notez bien que X est le nombre de jours encore
possible et non le total. |
Illustration
Bilan P = 150 P = 150 X = 150 (45 – 10) / 125 = 42 jours en plus Soit 52 jours de mission au total. |
|
Voir Équations
|
|
||
|
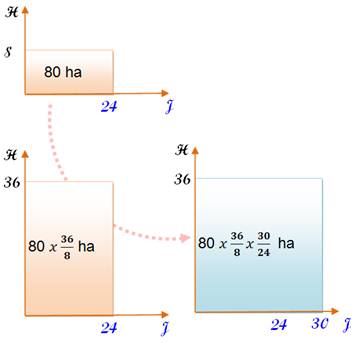
8 hommes fauchent 80 ha en 24 jours. Combien
36 hommes faucheront en 30 jours?
Au lieu
de 8 hommes, il y en a 36 pour faucher, soit 4,5 fois plus. La surface
fauchée sera nettement plus importante: Avec
la même équipe pendant plus de temps, elle fauchera encore plus de surface: 360 x
30 / 24 = 450 ha. |
Illustration
Bilan S = 80 x (36/8) x (30/24) = 450 ha |
|
|
|
||
|
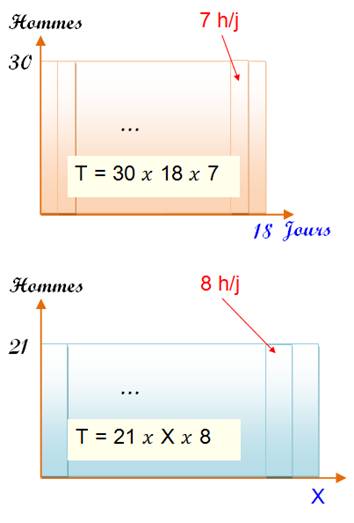
30 hommes en travaillant 7 heures par jour
terminent leur travail en 18 jours. 21 hommes en travaillant 8 heures par jour
mettront combien de temps?
T1 = 30 Et celle de la
seconde équipe: T2 = 21 Or, dans les deux
cas, il s'agit du travail pour terminer le travail T1 = T2 21 X = 22,5 jours Remarque: Il est plus facile et
plus sûr de passer par la démarche ci-dessus, plutôt que de trouver
directement les proportions données ci-contre |
Illustration
Bilan X =
18 |
|
|
Une
échelle est un rapport de réduction ou d'agrandissement, sans déformation. Échelle
au 1/100 000e (lire: un
cent millième) veut dire que 1 cm sur la carte représente 100 000 cm = 1 000 m = 1 km dans la
réalité. Si
on mesure 7,2 cm entre deux villes cela qu'elles sont distantes de 7, 2 km. Échelle
1/43e veut dire que 1 cm
représente 43 cm dans la réalité. Voici les dimensions d'une voiture
Mégane-Renault à cette échelle.
Échelle
20/1 ou plutôt grossissement de 20:
alors 20 cm mesurés représentent 1 cm en réalité. Un poil mesure 2mm à
travers une telle loupe; la taille du poil est donc: 2 / 20 = 0,1 mm. |
![]()
|
|
||
|
Problème Le prix
d'un article diminue de 5% puis augmente de10%. Quel la variation par rapport
au prix initial? |
Résolution P5 = P x 0,95 = P x 0,95 x 1,10 = P x 104,5 |
|
|
Problème Nous
inspirons 9 500 litres d'air par jour. L'air contient 20% d'oxygène. Seuls 5%
sont retenu par l'organisme. Quel le
volume d'oxygène retenu en une journée? |
Résolution Vair = 9 500 l VOx = 9 500 x 0,2 = 1 900 l VRetenu = 1 900 x 0,05 = 95 l |
|
|
Problème Prime de
22 725 euros à répartir entre trois services publics A, B et C selon la
fréquence hebdomadaire. Respectivement
125, 166 et 214 clients. Quelle
prime revient à chaque service? |
Résolution Subvention par clients: x Total subvention: 125x + 166x + 214x = 22 725 505 x = 22 725 x = 45 |
|
|
Problème Échelle
1/500 Salle de
10 cm par 12 cm Quelle
est l'aire réelle de la salle? |
Résolution Largeur: 10 x 500 = 5 000 cm
= 50 m Longueur: 12 x 500 = 6 000 cm =
60 m Aire: 50 x 60 = 3 000
m² |
|
|
Problème Un homme
pèse actuellement 72 kg. Il vient
de perdre 10% de son poids. Quelle
est sa perte de poids en kg? |
Résolution Pavant = X Pactuel = 72 = X – 0,1 X = 0,9 X X = 72 / 0,9 = 80 kg Perte: 80 – 72 = 8 kg |
|
![]()
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
Cette page |