|
||||||||||||||||||||||||||||
![]()
|
Introduction
Nom barbare qui,
comme souvent, cache des choses simples Certes, il est
possible de compliquer à loisir … Essayons de voir le
simple, d'abord!
|
Je connais déjà
un peu tout cela, montrez-moi la conclusion de cette page >>>
Pour commencer voir Échelle des puissances de dix
|
Utilisation en parallèle de DEUX échelles
de nombres
et
les puissances de 2 (progression Géométrique). |
||||||||||
|
A |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
G |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
|
On
ajoute les deux nombres parents sur la ligne A; On
cherche le "fiston" correspondant à la somme trouvée.
Exemple montrant qu'il suffit de lire la
table ci-dessus
|
||||||||||
|
A |
|
|
3 |
+ 4 |
|
= |
7 |
|
|
|
|
G |
|
|
8 |
x 16 |
|
= |
128 |
|
|
|
|
Un petit bout de théorie
2 x
. 2 y = 2 x + y
a x
. a y = a x + y |
||||||||||
Voir Archimède
/ Progressions / Puissance
Voir Notation
des grands nombres
|
|
||||||||||||||||||||||
|
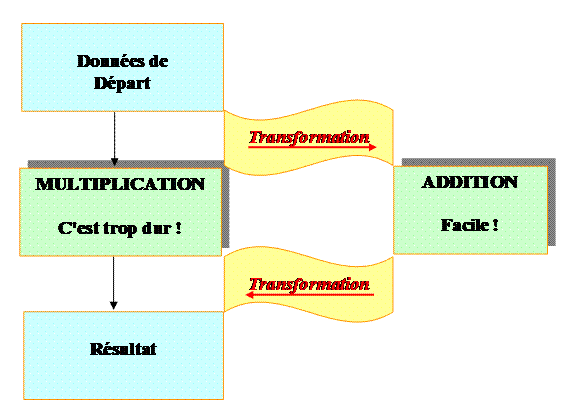
On peut tirer parti de cette observation
|
On transforme une MULTIPLICATION en ADDITION. |
|||||||||||||||||||||
|
Représentation des puissances de 10 1 000 = 103 10 000 = 104 10… 0 avec n zéros
= 10n |
L'exposant n indique la quantité de zéros derrière
le 1. |
|||||||||||||||||||||
|
Représentation des grands nombres 1 000 = 103 2 000 = 10 x 10 000 = 104 |
x existe-t-il ? Si oui, x est situé entre 3 et 4. |
|||||||||||||||||||||
|
Logarithme à base 10 2 000 = 10 3,3 3,3 = log (2000) |
Le nombre décimal obtenu est le LOGARITHME |
|||||||||||||||||||||
|
Exemples
|
||||||||||||||||||||||
Voir Nombre décimal
|
|
|||
|
Changement de monde Formule savante |
Pour MULTIPLIER on ADDITIONNE les LOGARITHMES
|
||
|
Morale de l'histoire: je n'y arrive
pas directement, alors je me sers d'un outil, d'un "levier"
mathématique. Exemples
|
|
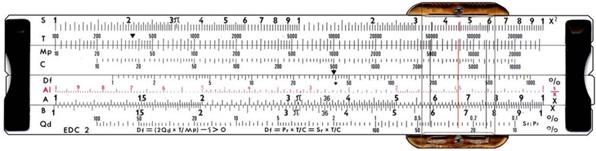
Allure d'une règle à calcul (ici Log-Log)
Ma
propre règle à calcul utilisée par ma petite-fille de 10 ans Un autre type (américaine)
Source: Number
Systems & Counting |
|
À LA FONCTION LOGARITHME |
|
|||||||||||||||
|
|
||||||||||||||||
|
|
|
|
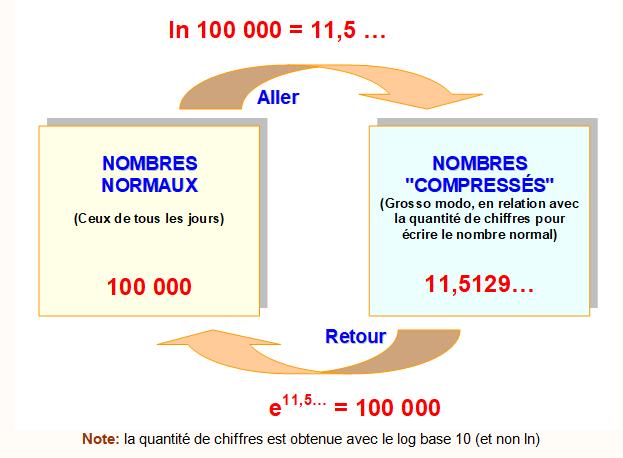
CE QUE NOUS DEVONS RETENIR
* Moins grands pour la partie entière;
avec les décimales, la quantité de chiffres peut être tout aussi grande que
pour le nombre d'origine (Voir exemple numérique sur illustration
ci-dessous)
C'est le cas, par exemple, du son
dont l'intensité sonore s'exprime en décibel,
une forme de logarithme. Les pas de deux hommes qui marchent ne font pas beaucoup plus de
bruits que ceux d'un seul marcheur. Par contre, une troupe qui marche, là
oui, il y a une belle différence. Le phénomène n'est pas simplement additif, mais plutôt multiplicatif,
comme dans le monde des logarithmes. Le fait est que, les lois physiques de ces phénomènes sont formulées
par des exponentielles. |
|
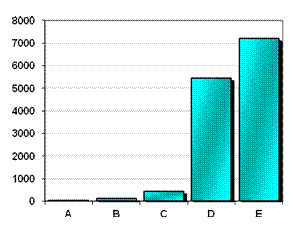
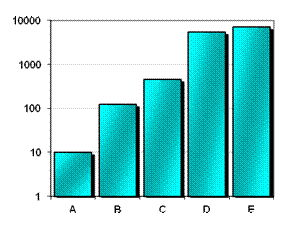
|
Échelle
normale
Échelle logarithmique
|
|
|
|
|
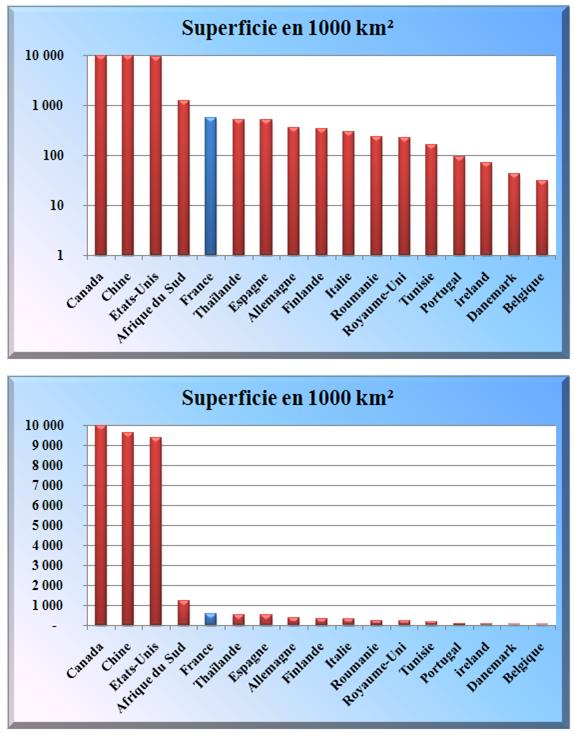
L'échelle
logarithmique (graphique du haut) fait ressortir les nuances des pays les
plus petits.
|
|
Voir Géographie
/ Les pays (junior)
En forme de bilan: technique opératoire
|
Puissances
de 10 Les
puissances de 10 sont faciles: elles indiquent la quantité de 0 derrière le
1. Ainsi: 102
= 100 et 103 = 1000 par exemple. Dans
ce monde, pour multiplier on ajoute et pour diviser on soustrait. 102 x 103 = 100 x 1000 = 100 000 = 105 = 102
+ 3 10a x 10b = 10a + b 103 / 102 = 1000 x 100 = 10 = 101 = 103
– 2 10b / 10a = 10b – a
C'est
un monde où les choses vont en se multipliant par 10. C'est
utile pour traiter les phénomènes comme l'audition. En effet, nos oreilles ne
sont pas linéaires, elles sont sensibles dans ce genre de rapport. Par
exemple, 2 bels (ou 20 décibels)
indique un rapport 100 entre deux puissances sonores.
Une puissance sonore qui double équivaut à 3 décibels. Exemple de calcul avec logarithmes
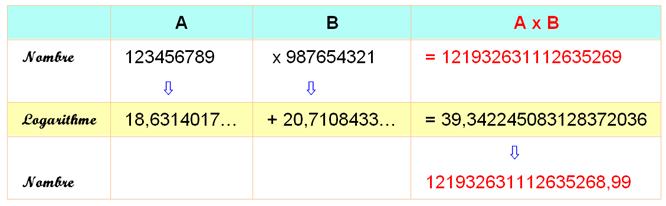
En
présence de très grands nombres, la calculette ne sait plus calculer; avec
les logarithmes, on s'en sort. |
Âge du chien comparé à celui des humains
|
L’Université de Californie à San Diego
(États-Unis), après étude de l’influence de l’ADN sur l’âge des Labradors (épigénétique), propose une formule
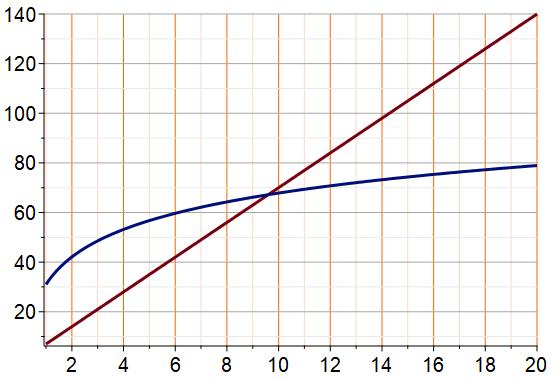
comprenant un logarithme : H = 16 ln
C + 31 Graphe : âge équivalent humain du chien
On donnait 2 x 7 = 14 ans à un chien de 2 ans ; |
Presse américaine de novembre 2019 –
New Formula Reveals Your Dog’s Real Age In Human Years
Voir Âge deviné / Âge de Diophante
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()