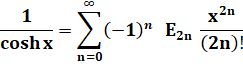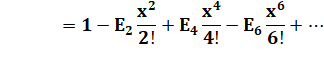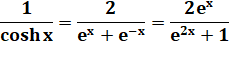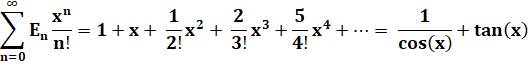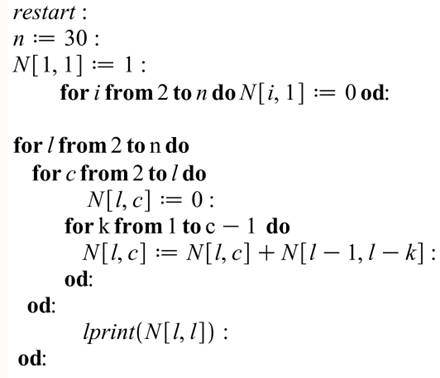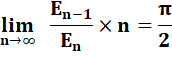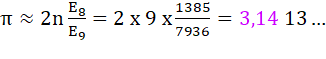NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/12/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Type de NOMBRES
Débutants Nombres	NOMBRES d'EULER			Glossaire Nombres
INDEX Type de Nombres Théorie des Nombres	Permutations alternées	Euler – Zigzag	Totient d'Euler		Gamma
		Sommaire de cette page >>> Nombres d'Euler >>> Valeurs numériques >>> Méthode de calcul >>> Programme de calcul >>> Propriétés >>> Anglais

NOMBRES d'EULER

ou nombres sécants

ou nombres zigs

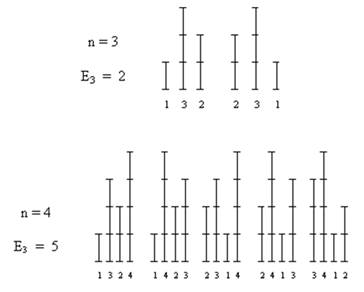
Variété de nombres résultant du développement limité de la fonction sécante, autre nom de l'inverse du cosinus. Ces nombres reflètent la quantité de façons d'arranger les nombres entiers en mode zigzag.

Note: Euler a été si prolixe que de nombreux types de nombres portent son nom.

Voir: nombre zigzags, zigs ou zags >>>

Voir Page introductive sur ces nombres

Nombres d'EULER
Famille	Nombre / Théorie des nombres
Approche	Notion très avancée de la théorie des nombres. Nombres définis par le développement d'une série entière.
Définition	NOMBRES d'EULER de première espèce ou nombres sécants Ils sont définis par un développement en série de Taylor: La fonction sécante est l'inverse de la fonction cosinus. D'où le nom parfois donné à ces nombres.
Valeurs	Suite en A000364

Définition avec signes	Alternative avec signes Développement en série avec une sécante hyperbolique ou inverse du cosinus hyperbolique: Il s'agit du développement en série entières de:
Valeurs	Suite en A028296

Valeurs numériques
Voici le calcul du développement de 1/ cos (x) en fractions et en valeurs numériques, jusqu'au 24^e terme. Chaque terme, multiplié par n!, donne un nombre d'Euler. Ex: avec le terme en x^8 qui vaut 277 / 8064, multiplié par 8! = 40 320 donne bien 1385.

Calcul des nombres d'Euler

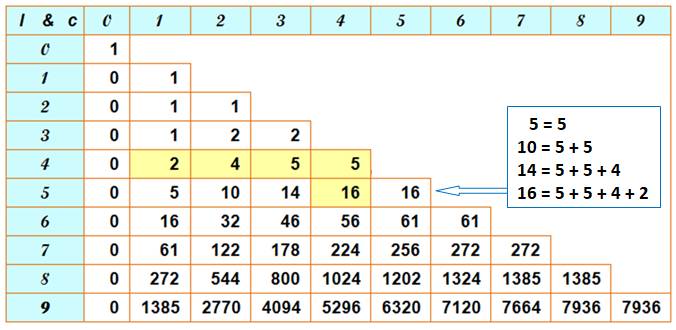
Règle de construction On construit un tableau lignes (l) et colonnes (c). Le remplissage est effectué selon les instructions suivantes: dans la première colonne tous les nombres sont 0, sauf le premier qui vaut 1. un nombre en colonne c est égal à la somme des c nombres de la ligne du dessus (l – 1), en partant de la droite. Table de construction Les nombres en colonne 1, comme sur la diagonale, sont les nombres d'Euler, en en sélectionnant un sur deux. Voir une idée du pourquoi de cette méthode en Table des nombres zigzags Génération informatique Programme basé sur la méthode de construction exposée ci-dessus. Les nombres d'Euler sont ceux marqués en jaune. Liste: 1, 1, 5, 61, 1385, 50521, 2702765, 199360981, 19391512145, 2404879675441, 370371188237525, 69348874393137901, 15514534163557086905, 4087072509293123892361, 1252259641403629865468285, 441543893249023104553682821, 177519391579539289436664789665, … Nombres zigs et nombres zags Cette construction montre tous les nombres dits zigzags. >>> En jaune les nombres zigs ou nombre sécants ou nombres d'Euler. Tous impairs. Les autres sont les nombres zags ou nombre tangents. Tous pairs, sauf le premier. Ils sont présents dans le développement en série de la fonction tangente. Leur définition fait appel aux nombres de Bernoulli (Voir informations avancées). Note: tous les nombres zigzags sont les coefficients du développement suivant:

Programme (Maple) et commentaires
	n est la quantité de nombres calculés. N est le tableau ligne (l) et colonne(c). Il est initialisé sur sa première colonne. Balayage en ligne et colonne Initialisation à 0 de la cellule du tableau qui va être calculée. Le pointeur k sert à désigner les c cellules à additionner. Les bornes sont toujours délicates à déterminer. Toujours s'assurer que ce sont les bonnes en testant les premières valeurs. Impression de la valeur sur la diagonale.
Aucune difficulté pointue de programmation pour élaborer ce programme. Cependant, un bon exercice pour la maîtrise des boucles (ici trois balayages: l, c et k) et des limites de pointeurs de boucles. Note: il est plus simple d'utiliser la fonction "euler" de Maple qui donne directement ces nombres; mais, alors, ce n'est plus du jeu! euler(100) donne 2,9… 10^138 = 290352834 6661097497 0546038347 6443587507 7553006646 1589450804 9231914699 7643370625 0238893534 4712996735 4174648294 7485105535 2869245763 2980625125 .

Voir Programmation Maple

Propriétés

Premiers Les nombres d'Euler sont peu nombreux à être premiers: le n°4: 5 le n°6: 61 le n°38: 234895805270431082520178285761989 les suivants: n°454, 510 … Rapport des nombres zigzags Ex: Nombres zigzags Les nombres d'Euler donnent la quantité de façons de ranger les n premiers nombres en zigzag: un grand, un plus petit, un plus grand, à nouveau un plus petit, etc. n1 < n2 > n3 < n4 > n5 < … Exemples

Suite en Table des nombres zigzags / Voir Nombres ondulants

English corner
The Euler numbers or secant numbers are a sequence En of integers defined by a Taylor series expansion. They also occur in combinatory theory, specifically when counting the number of zigzag permutations, a specific case of odd alternating permutations.

Merci à Claude Morin pour sa contribution

Suite	Euler – Index Nombres premiers d'Euler Nombres Boustrophédon Nombres oscillants
Voir	Euler – Biographie Nombres croissants Type de Nombres – Index
DicoNombre	Nombre 2
Site	Autres propriétés avancées en Euler Number – Weisstein Tangent Number – Weisstein OEIS A000364 - Euler (or secant or "Zig") numbers: e.g.f. (even powers only) sec(x) = 1/cos(x)
Cette page	http://villemin.gerard.free.fr/aNombre/TYPTHNOM/Euler.htm