|
||||||||||||||||||||||||||||||||||||||||
![]()
|
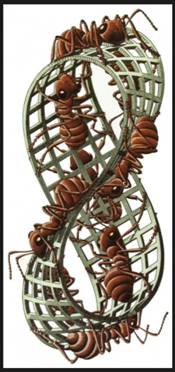
CURIOSITÉS TOPOLOGIQUES Le ruban de Moebius, la bouteille de Klein … Des objets curieux pour lesquels le dedans est dehors …
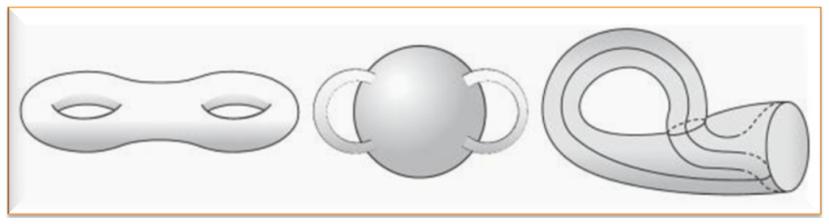
La
sphère n'a pas de trou, le tore
en a un, le
double tore, deux et le triple tore, trois. |
|
|
|||
|
En découpant le long de la ligne
médiane, on obtient un seul morceau formant quatre demi-tours
Voir Ruban de Moebius / Infini / Problème du carré inscrit
/ Spineur |
Cette surface n'a qu'une seule face. Elle est inorientable. Sur un tel
circuit, une voiture parcourait la partie blanche puis la partie sombre sans
difficulté.
|
||
|
Question Problème du ruban de Moebius posé en 1977
par Charles Weaver and Benjamin Halpern. Quel est le rapport de taille minimum entre
la largeur et la longueur du ruban tel qu'il soit réalisable sans pliures ? Ce serait autour de √3 ≈ 1,73… |
Nouveauté 2023 Pour les proportions autour de racine de 3,
l'existence d'intégrations lisses, sans auto-intersection, reste un problème
ouvert.. En
2023, Richard Schwartz a annoncé une preuve de leur inexistence. Si l'exigence de douceur est assouplie pour
permettre des surfaces continuellement différenciables, le théorème de
Nash-Kuiper implique que deux bords opposés de n'importe quel rectangle
peuvent être collés pour former une bande de Möbius intégrée, quel que soit
le rapport hauteur/largeur. |
||
|
|
|
|
|
Source image: Lozère
modélisme |
Ang: Moebius strip
|
Le ruban de Moebius (ou Möbius; Möbius strip) est
une surface non orientable à deux
dimensions avec seulement une face quand elle est plongée dans un espace
euclidien à trois dimensions. Ruban fermé par collage après un demi-tour de la
bande (ou un nombre impair quelconque
de demi-tours. Dans tous les cas, la bande offre une seule surface. Il a été découvert en 1858 par le mathématicien
allemand August Möbius (1790-1868) et, simultanément, par Johann Listing
(1808-1882). Listing est le premier à employer le mot topologie, au lieu du terme Ce ruban a fasciné les artistes comme Esher (Illustration). Il a joué un rôle fondamental dans la création de
la topologie, la géométrie qui étudie les propriétés des objets qui se
déforment et s'étirent. Domaine à forte implication dans la théorie des cordes, par exemple. |
Voir Contemporains
English corner
|
The Möbius strip is a one-sided
object that can be made by simply twisting a piece of paper and connecting
the ends with some tape. If you were to follow the loop around with your
finger, you'd eventually end up right
back where you started, having touched the entire surface of the loop along
the journey. This simple creation, the Möbius strip, is fundamental to the entire
field of topology and serves as a quintessential example of various
mathematical principles. |
Voir
Anglais pour le bac et pour les affaires
|
|
||
|
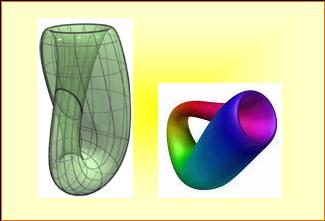
Voir Bouteille de Klein |
|
|
Ang: Klein bottle

|
|
||
|
|
Impossible d'inverser la face bleue et la face blanche selon les lois
de la topologie. |
|
|
|
||
|
|
Aucun dessin ne permet de visualiser l'opération. même les vidéos
peinent. |
|
|
|
||
Double tore / Sphère à deux poignées
/ Bouteille de Klein
Anneaux de Moebius et la
sculpture



Aase Texmon Rygh Mobius – 19
Merci à
Évelyne
![]()
|
Voir |
|
|
|
Aussi |
|
|
|
Sites |
Cherchez "To
turn the sphere upside down" sur YOUTUBE
|
|
|
Cette page |
||
![]()