NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/07/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Constructions des TRIANGLES			Glossaire Triangle
INDEX Triangle Constructions	Types de triangles	Constructions élémentaires des triangles
	Constructions	Orientation	Avec bissectrices
	Résolution des triangles	Quelconque	Quadrature
		Sommaire de cette page >>> Orientation (LLL, LAL, etc.) >>> Tracé d'un vrai triangle quelconque

TRIANGLES QUELCONQUES

Construction

Comment dessiner un triangle quelconque?

Avec quels instruments? Faut-il faire des calculs?

Pour être capable de dessinez un triangle, il faut connaître trois éléments – longueur (L) des côtes ou angles (A) – dont au moins une longueur de côté.

Construire un triangle en connaissant la longueur (L) des trois côtés est une construction LLL.

La construction du triangle AAA, étant donnés les trois angles, conduit à une infinité de triangles semblables. Voir Explications

La construction avec la règle et le compas seulement n'est pas toujours faisable, notamment pour construire les angles de valeur quelconque. Nous auront recours à la trigonométrie.

Index CONSTRUCTION du Triangle

Par rubriques principales

Général

Le triangle: types, droites remarquables, …

Triangles égaux (congrus)

Triangles semblables

Résolution des triangles

Longueurs des côtés (L) et Angles (A)

Constructions élémentaires: les triangles – Introduction

	3 côtés	2 côtés
	LLL	LAL	LLA
Quelconque	>>>	>>>	>>>
Rectangle	>>>	>>>	>>>
Isocèle	>>>	>>>	>>>
Équilatéral	>>>	>>>	>>>

	1 côté		Aucun côté
	ALA	AAL	AAA
Quelconque	>>>	>>>	>>>
Rectangle	>>>	>>>
Isocèle	>>>	>>>
Équilatéral	>>>	>>>

Autres constructions particulières: voir index constructions

Hauteur

La Hauteur

Rectangle

Construction du triangle quelconque

TRACÉ d'un vrai triangle quelconque
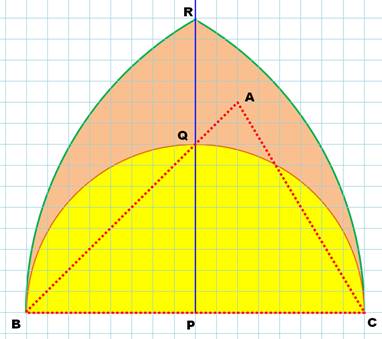
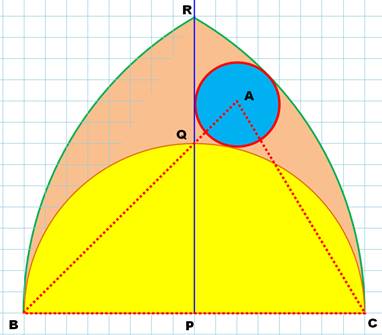
Tracer un triangle quelconque à angles aigus: ni rectangle, ni isocèle. Pas si facile qu'il y paraît! 1. Si A est sur le demi-cercle BQC, il est rectangle; 2. Si A est sur la médiatrice PR, le triangle est isocèle; 3. Si A est sur les arcs BR ou CR, le triangle est isocèle; et 4. Si A est à l'intérieur du demi-cercle BQ, l'angle A est obtus. Le point A doit se trouver dans la zone marron (BQR ou CQR). Pour dessiner ce triangle quelconque, il vaut mieux s'éloigner des frontières. Le meilleur endroit est le centre du cercle indiqué en bleu. Oups! Le point A est alors sur la droite BQ ou CQ et alors, un des angles est égal à 45°. Le triangle n'est pas si quelconque!	Le point A placé dans la zone marron a toutes les chances de former un triangle ABC quelconque à angles aigus.

Construction du triangle quelconque LLL
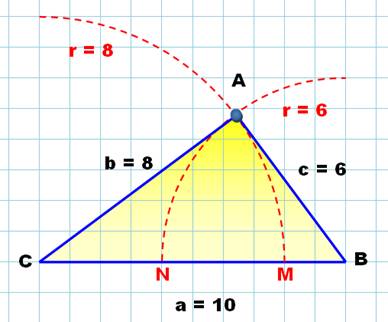
Trois côtés connus Dessinez le triangle dont les côtés mesurent: 10, 8 et 6 unités. On vérifie que le plus grand côté a une longueur inférieure à la somme des longueurs des deux autres, sinon, les côtés seraient trop cours et ne se rejoindraient pas. On commence par tracer un segment BC de 10 unités, on marque les points M et N à 8 et 6 unités en partant de C pour l'un et de B pour l'autre. De C, on trace le cercle de rayon CM = 8 unités et de B, on trace le cercle de rayon BN = 6 unités. Le point d'intersection A est le troisième sommet du triangle demandé. Note: pour dessiner un triangle quelconque, il faut connaitre trois éléments parmi les trois côtés et les trois angles dont au moins la longueur d'un des côtés.	Pour dessiner le triangle (10, 8, 6), tracez un segment de 10 unités et deux cercles de 8 et 6 unités. Notez que ce triangle, supposé quelconque est en fait rectangle en A. En effet: 10² = 8² + 6² = 100 (Pythagore).

Voir Résoudre le triangle quelconque

Construction du triangle quelconque LAL
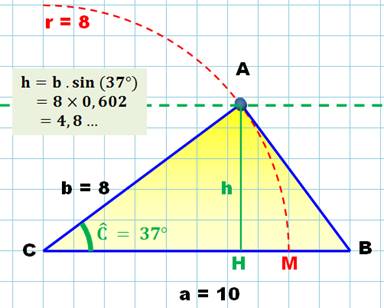
Deux côtés et l'angle inclus Dessinez le triangle avec deux côtés de 10 et 8 unités faisant un angle de 37°. Comme précédemment, on dessine BC = 10 unités et le cercle de centre C et de rayon égal à 8 unités. Maintenant deux possibilités pour tracer l'angle: 1. Directement avec le rapporteur (vous savez faire) 2. En calculant la longueur de la hauteur h. Je vous montre comment faire avec une calculette. La hauteur AH est le côté opposé à l'angle du triangle rectangle ACH. Sa longueur est égale à l'hypoténuse multipliée par le sinus de l'angle. Tapez 37 sur la calculette (réglée sur les degrés), puis sur sin; elle vous donne: 0,60181 … C'est la proportion de la hauteur par rapport à l'hypoténuse. h = 0,602 x 8 = 4, 8 unités Dessiner la droite parallèle à BC (pointillés verst) et à une distance de 4,8. Son intersection A avec le cercle (pointillés rouges) est le troisième sommet du triangle demandé.	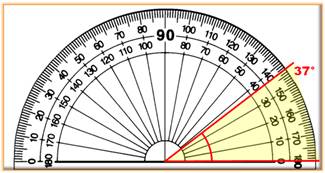Construction Connaissant l'angle de 37°, on calcule la longueur de la hauteur AH. Mesure de 37° avec le rapporteur Anglais: Protractor Exemple de calcul du sinus avec la calculette de votre ordinateur

Construction du triangle quelconque LLA
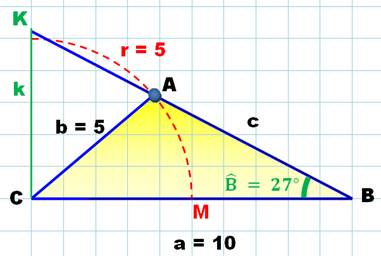
Deux côtés et l'angle exclus Dessinez le triangle avec deux côtés de 10 et 5 unités. L'angle B étant égal à 27° Dessinez BC = 10 unités et le cercle de centre C et de rayon égal à 5 unités. Pour dessiner l'angle, la règle et le compas ne sont pas suffisent pas. Il faut un rapporteur ou alors la calculette. Dans le triangle BCK: tangente B = k / a. k = a . tan (27°) = 10 x 0,509 = 5,09 unités. Soit la construction: on dessine CK perpendiculaire à CB est de longueur 5, 1 unités. La droite KB coupe le cercle en A, le troisième sommet du triangle demandé	Construction La valeur k dans le triangle rectangle BCK est liée à la tangente de l'angle en B. Note: avec un angle de 26,565° nous aurions une valeur de k exactement égale à la moitié de a.

Construction du triangle quelconque ALA
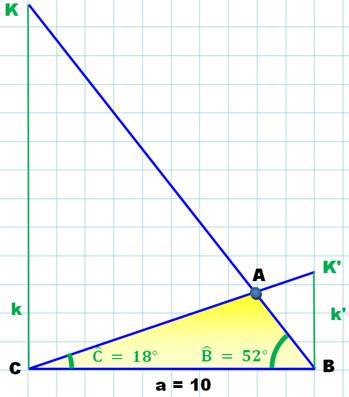
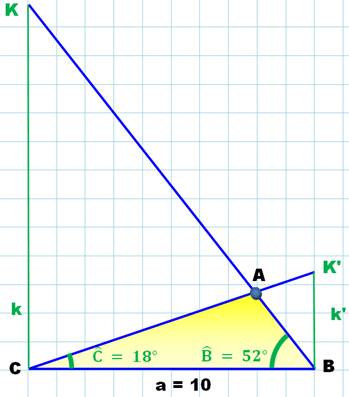
Deux côtés et l'angle exclus Dessinez le ayant une côté mesurant 10 unités. Les deux angles adjacents étant de 18° et 52°. Dessinez BC = 10 unités. Comme précédemment, on dessine les références K et K' correspondant aux tangentes des angles. k = a . tan (52°) = 10 x 1,28 = 12,8 unités. k' = a . tan (18°) = 10 x 0,325 = 3,25 unités. Les droites BK et CK' se coupent en A, le troisième sommet du triangle demandé. Le cas AAL se ramène au cas ALA, car connaissant deux angles le troisième est connu:	Construction Les segments CK et BK' sont perpendiculaires à BC et de longueur proportionnelle à la tangente des angles.

Suite	Construction connaissant les bissectrices
Voir	Aire égale pour trois triangles dans un rectangle Allumettes Angle Carrés Centre de gravité Cercles Droite Égalités des triangles Jeux Polygones Probabilité d'obtenir un triangle obtusangle Quadrupler le triangle Résolution du triangle quelconque Symétries Triangle – Index Triangle de Pythagore Types de triangles
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Calcul/ConsQuel.htm