|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
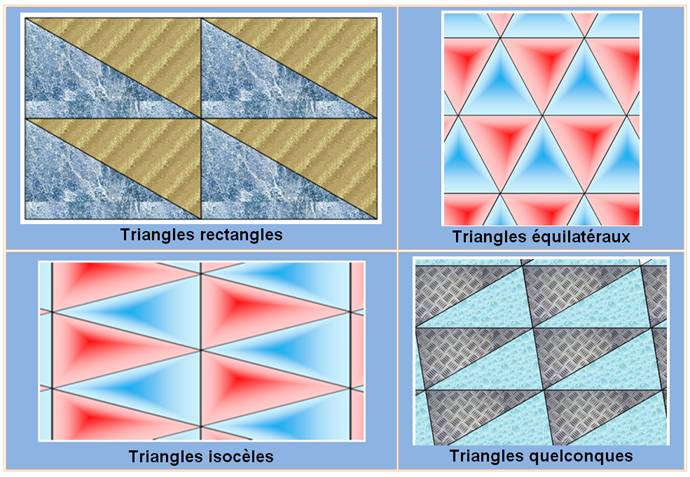
Pavage avec les CARRÉS, RECTANGLES et TRIANGLES Une introduction au problème du
pavage
Le pavage consiste à recouvrir une surface
avec des pièces de formes données, comme on le fait en réalisant un puzzle.
Pas de chevauchement, pas d'espaces on recouvert. Le pavage le plus simple est celui
du carreleur avec des carreaux de forme
carrée ou rectangulaire. Cette page est une introduction au problème géométrique du pavage. LA forme utilisée et le triangle. |
Anglais: Jigsaw puzzle
Voir Pavage –
Une approche via les trasnformations
|
|
||
|
Pavage avec des carrés Une seule possibilité |
|
|
|
Pavage avec des rectangles Nombreuses possibilités
Pavage mixte, avec des carrés et des rectangles Nombreuses possibilités
|
||
Voir Carrés et rectangles / Pavage
carré parfait
Voir Triangle
|
|
||
|
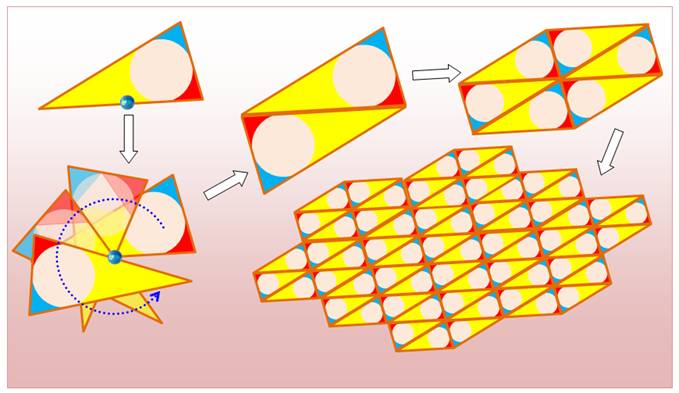
Partant d'un triangle quelconque, en
créer un autre par rotation de 180° autour du point milieu d'un des côtés
(point bleu). Ces deux triangles forment un parallélogramme. Le pavage est
créé en collant plusieurs de ces formes entre elles. Étapes de la construction
|
||
|
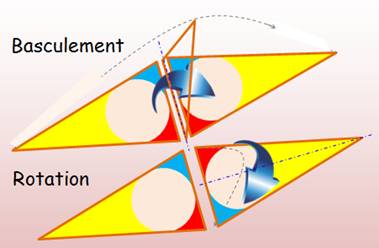
Chaque nouveau triangle est le même que celui qui
lui est adjacent par l'un de ses côtés en le basculant de l'autre côté et en
le faisant pivoter. |
|
|
|
Cette construction est toujours possible quel que
soit le triangle. Ceci est dû à la propriété de tout triangle: La somme de ses trois angles est égale à 180°. |
|
|
|
|
||
|
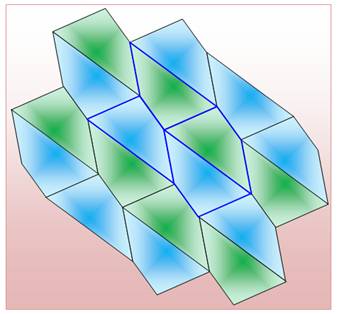
Comme pour le triangle, et parce que la somme des angles est égale
à 360%, il est possible de paver le plan avec un quadrilatère quelconque. La maille répétitive, formée de quatre
quadrilatères ayant pivotés, est marquée en bleu foncé. |
|
|
Voir Quadrilatère
|
Le
pavage du plan est toujours possible avec les triangles et les quadrilatères
de toutes natures, c'est-à-dire avec les polygones à trois et quatre côtés.
Et pour les autres? Nous
verrons qu'il existe de nombreuses possibilités mais que ce n'est pas toujours
possibles pour les polygones réguliers. |
|
|
||
|
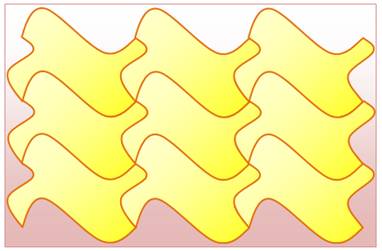
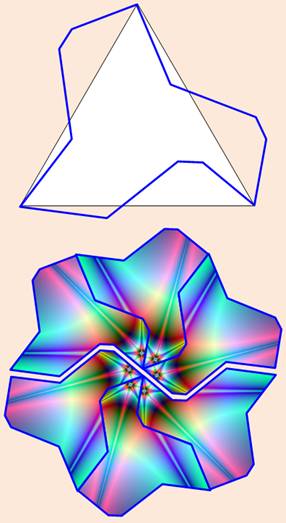
Dessin itératif, typique de Maurits Cornelis Escher
(1898-1972). Il disait: recouvrir le plan est devenu une réelle manie addictive et
j'ai parfois du mal à m'y arracher. Le principe de construction de ces dessins de
base est simple, le reste st dû à la créativité de l'artiste. |
|
|
|
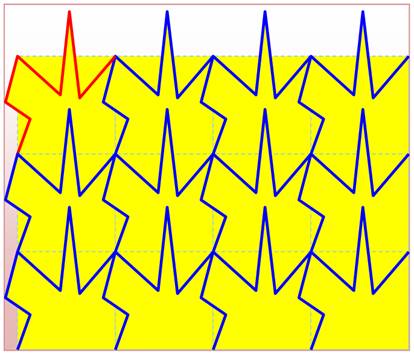
Un des principes, à base de carrés 1) Réalisez un quadrillage carré (bleu
pointillé); 2) Dessinez une ligne passant par trois sommets,
laissant le quatrième en bas à droite libre (ligne rouge). 3) Répétez cette ligne dans le quadrillage. |
|
|
|
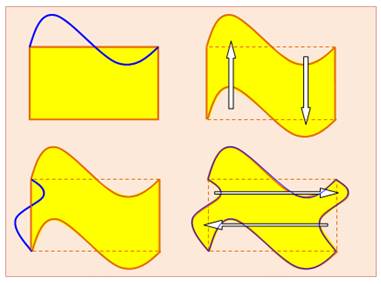
Réalisation pratique Pour réaliser une pièce du pavage (du puzzle): 1) Dessinez un rectangle
(ou un parallélogramme)
dans de la cartoline (papier cartonné); 2) Tracez une ligne entre les deux sommets du
haut: ligne courbe, brisée, sortante, rentrante. 3) Copiez cette courbe entre les deux sommets du
bas. 4) Pratiquez une opération semblable pour les
bords verticaux. 5) Découpez la pièce et reproduisez la autant que
vous voulez. Elles s'emboitent entre elles. Certains découpe
un rectangle, puis les parties n creux
et les colle avec du ruban adhésif pour former les partie saillantes. Cas du triangle Appliquez la même méthode en déformant un côté en
une ligne à votre goût et reproduire cette courbe su les deux autres côtés. Avec cette méthode, la somme des angles est conservée et six telles
pièces s'assemblent pour former un angle complet de 360°. |
|
|
|
|
||
|
Problème Comment disposer un minimum de ce type de triangle rectangle pour
obtenir un carré ? Comment faire un carré avec vingt de ces
triangles ? |
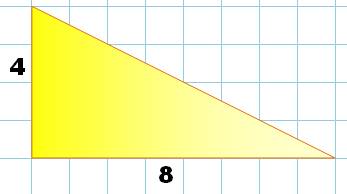
Le triangle à utiliser
|
|
|
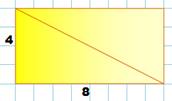
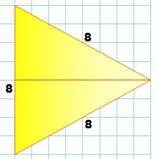
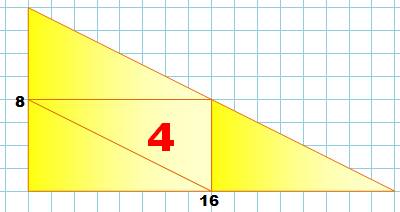
Carré Nous remarquons qu’il s’agit d’un triangle rectangle qui,
par deux, forment : - Un rectangle 4 x 8, ou - Un triangle
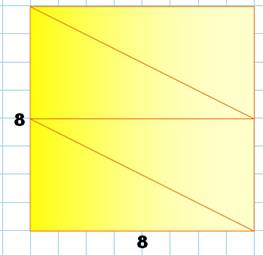
isocèle de côté8. Pour former un carré 8 x 8, il suffit de doubler le
rectangle. Seuls quatre triangles suffisent. Quatre tels carrés assemblés forment un carré plus grand.
Son côté vaut 16 et il faut 16 triangles. Avec cette méthode, impossible de
créer un carré avec vingt triangles. Comment s’y prendre, alors ? |
|
|
|
Triangles semblables Comment former un triangle plus grand semblable
à l’original ? Un assemblage de quatre
triangles fera l’affaire. Évidemment pas question de trouver un assemblage de ces
grands triangles selon la méthode précédente pour trouver un carré. Il faut une astuce ! |
|
|
|
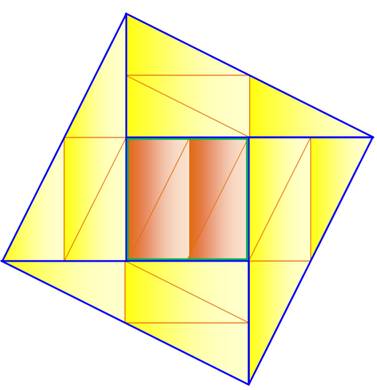
Carré avec vingt triangles La solution consiste à assembler quatre grands triangles
(contours bleus) comme indiqué et à combler le carré central (vert) avec le
grand carré vu plus haut. Le grand carré compte alors : 4 x 4 + 4 = 20 triangles. La longueur de son côté (C) est égale à deux fois
l’hypothénuse (H) de chaque triangle élémentaire : Calcul H² = 4² + 8² = 16 +
64 = 80 H = 8,94427 ... C = 17,88854... |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Sites |
|
|
Cette page |
![]()