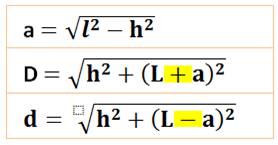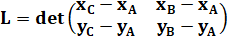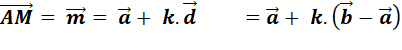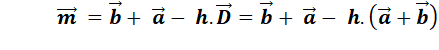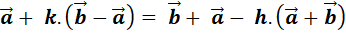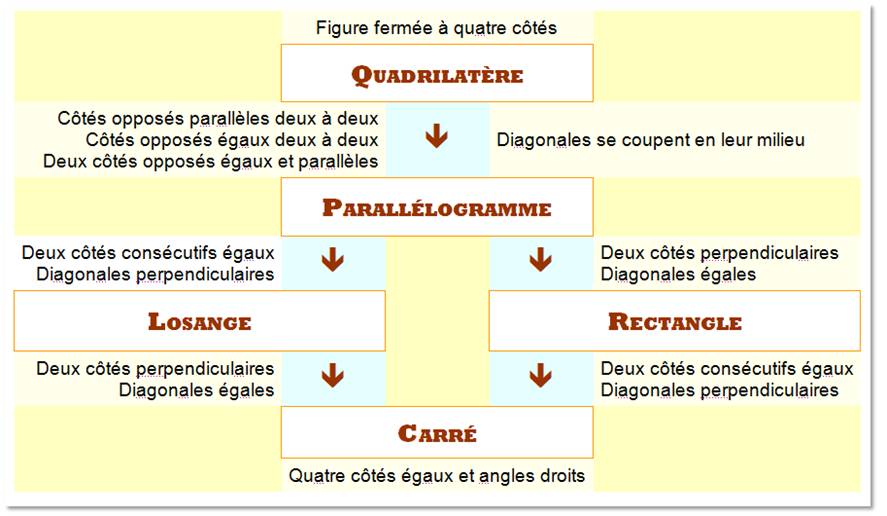
NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/07/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ÉLÉMENTS de base
Débutants Géométrie Junior Découverte des quadrilatères	Généralités				Glossaire Géométrie
INDEX Polygones et polyèdres Géométrie	Quadrilatère	Carré		Trapèze
	Parallélogramme	Carré – Propriétés		Losange
	Parallélogramme – Toutes les formules			Rectangle
	Parallélogramme divisé – Calcul d'aires		Parallélogramme et octogone
		Sommaire de cette page >>> Propriétés >>> Aire >>> Étude de parallélogrammes >>> Curiosités – Théorèmes >>> Parallélogramme et triangle rectangle >>> Partage du parallélogramme >>> Aire analytique (vecteurs) >>> Diagonales et milieu – Démonstration

PARALLÉLOGRAMME Quadrilatère plan dont les côtes sont parallèles deux à deux. Parallélogrammes particuliers: rectangle, losange et carré Note: le parallélogramme est utilisé dans les organigrammes (description d'algorithmes) pour désigner une entrée de données.

Hexagone formé de 12 parallélogrammes (losanges)

Anglais: Parallelogram: A quadrilateral that contains two pairs of parallel sides.

A four-sided plane figure that has two sets of opposite parallel sides.

La famille

Voir Parallélépipède et sa famille

Ce qu'il faut savoir du parallélogramme

Un parallélogramme a:

ses côtés opposés sont parallèles;

ses côtés opposés 2 à 2 de même longueur;

ses angles opposés 2 à 2 de même mesure;

ses angles adjacents sont supplémentaires (= 180°)

ses quatre angles totalisent 360°

ses diagonales, inégales, se coupent en leur milieu;

chaque diagonale partage le parallélogramme en deux triangles égaux >>>

les deux diagonales divisent le parallélogramme en deux paires de triangles égaux >>>

la somme des carrés des diagonales égale la somme des carrés des côtés >>>

pour centre de symétrie l'intersection de ses diagonales.

les bissectrices des angles opposées sont parallèles >>>

les bissectrices de deux angles adjacents sont perpendiculaires >>>

les quatre bissectrices délimitent un rectangle >>>

C'est un parallélogramme si:

un quadrilatère* a ses côtés opposés deux à deux de même mesure;

un quadrilatère* a ses angles opposés deux à deux de même mesure;

un quadrilatère* a deux côtés opposés parallèles et de même longueur;

un quadrilatère* a ses diagonales qui se coupent en leur milieu;

un quadrilatère* a un centre de symétrie;

un quadrilatère* à deux côtés parallèles et de même longueur;

un trapèze à ses côtés parallèles;

* quadrilatère non croisé.

Ce n'est pas obligatoirement un parallélogramme si:

un quadrilatère à deux côtés opposés de même longueur et deux angles opposés égaux >>>

Voir Démonstration du théorème des points milieux du triangle

PROPRIÉTÉS
Côtés opposés Parallèles Mêmes longueurs	AB = CD AD = BC
Angles opposés Égaux	AABC = ACDA ABCD = ADAB
Angles consécutifs Supplémentaires	AABC + ABCD = 180°
Aire Base par hauteur	Aire = L . h
Règle du parallélogramme Somme des carrés de tous les côtés = somme des carrés des diagonales
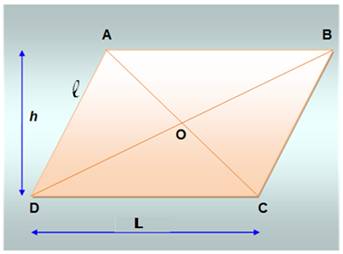
Diagonales (Figure ci-dessous)

Voir Toutes les autres formules du parallélogramme / Exemple de calculs

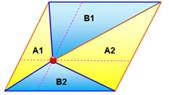
Triangles formés par les diagonales

Les diagonales partagent le parallélogramme en quatre triangles d'aires égales.

Angles alternes internes égaux.	AABD = ABDC
Même milieu O. Médiane de l'autre. Centre de symétrie du parallélogramme.	OA = OC OB = OD
Grands triangles égaux. Deux côtés de même longueur. Un angle égal. Aire égale à la moitié de celle du parallélogramme.	ABD = BCD = CDA = DAB
Petits triangles égaux. ABC et DCD sont égaux. OBC est une partie commune. Les deux parties restantes sont égales.	OAB = OCD = OBC = OAD

Suite >>>

Triangles avec les médianes

Tous ces triangles notés de 1 à 8 couvrent un quart de la surface du parallélogramme. De même, les huit autres en prenant les autres diagonales.

Voir Application

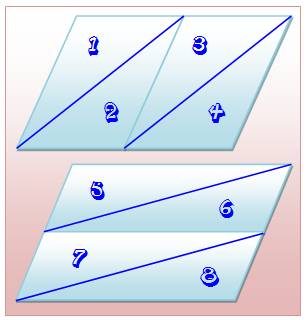
Cercle circonscrit

Cercle inscrit

Seul le carré possède les deux; le rectangle n'a que le cercle circonscrit.

AIRE
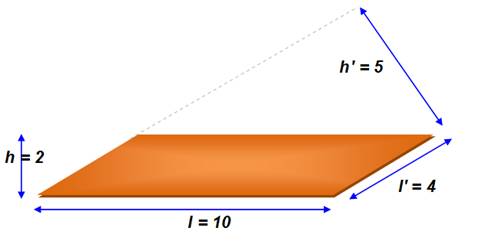
L'aire du parallélogramme est égale au produit des mesures de la longueur d'un côté par la hauteur issue de ce côté. A = l . h = l' h'	A = l × h where the base l is any side, and the height h is the distance between the lines that the sides of length B lie on.
	Deux possibilités pour calculer l'aire: A = 10 x 2 = 4 x 5 = 20
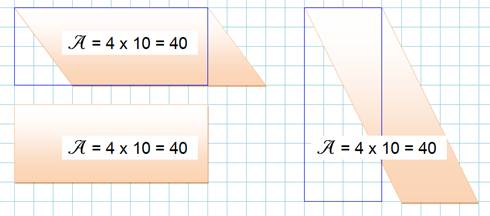
	Elle est équivalente à celle d'un rectangle de côtés l et h dans un sens ou dans l'autre.
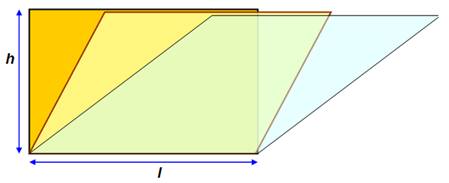
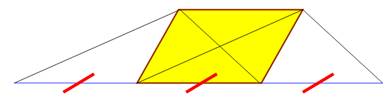
	Tous les parallélogrammes de côté l et hauteur h ont même aire A = l . h Parallelograms on the same base and between the same parallels are equal in area.
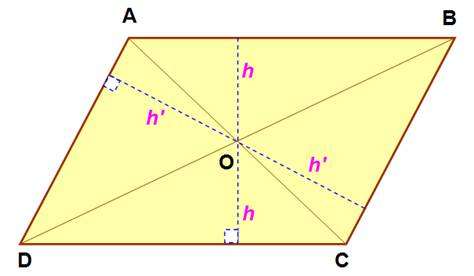
	Les quatre petits triangles découpés par les diagonales ont même aire. Aire du parallélogramme ABCD = 2h . AB = 2h' . BC En divisant par 4 ½ h . AB = ½ h' . BC Or ce sont les aires des triangles: Aire(ABO) = Aire(BCO)

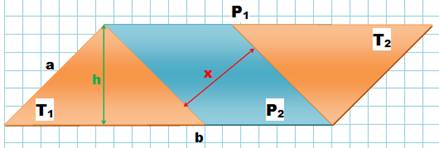
		Application pratique: calculez la distance x sur cette figure.
Comparaison des aires: P1 = T1 + P2 + T2 Évaluation de chacune de ses aires et mise en évidence de la valeur de x.

Voir Calcul vectoriel de l'aire

Étude de parallélogrammes
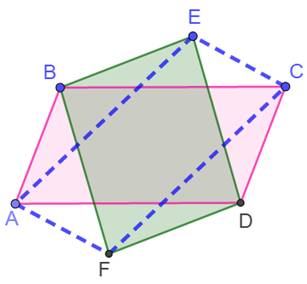
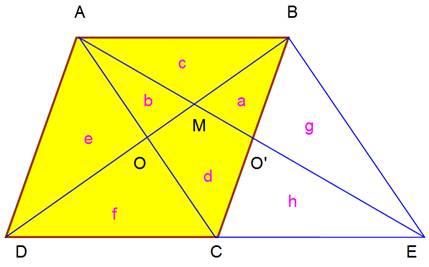
Énoncé Deux parallélogrammes ABCD (rose) et BEDF (vert). Nature du quadrilatère AECF (bleu) ? Dans les triangles ABE et CFD, deux paires de côtés ont mêmes mesures (AB = CD et BE = DF). Les angles ABE et CDF, formés par des droites parallèles, sont égaux. Deux côtés et un angle de mêmes mesures, les triangles ABE et AFD sont égaux (superposables). Alors, les angles BAE et FCD sont égaux; les droites AB et CD étant parallèles, les droites BE et FD, autre côté des angles, sont parallèles aussi. Même raisonnement pour les droites BF et ED. Le quadrilatère AECF a ses côté parallèles deux à deux, c'est un parallélogramme.

Curiosités – Théorèmes
	Trois parallélogrammes siamois (de même aire). Ils sont construits sur la base des deux diagonales. Base: les trois segments cochés en rouge sont de même longueur. Hauteur: d'évidence la même.
	Un quadrilatère quelconque. Le milieu de chaque côté. Le nouveau quadrilatère formé est un parallélogramme Théorème de Varignon (1654-1722)

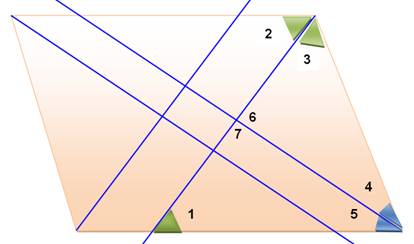
Les quatre bissectrices délimitent un rectangle Les bissectrices sont parallèles deux à deux => parallélogramme. Suivons les angles: 1 = 2 car alternes internes. 2 = 3 car bissectrice 4 = 5 car bissectrice 1 + 5 + 7 = 180 ° car somme des angles 4 + 3 + 6 = 180° 6 – 7 = 0 car résultat de la différence Les angles 6 et 7 sont égaux et leur somme vaut 180°, chacun vaut 90°. Le parallélogramme a ses angles droits, c'est un rectangle.

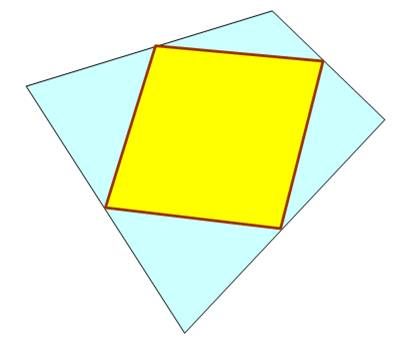
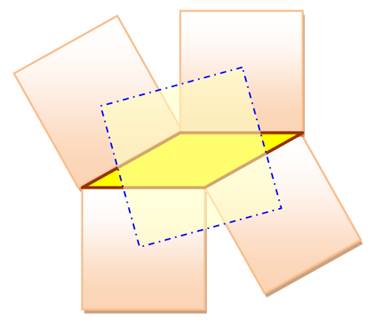
Un parallélogramme et les carrés formés sur chacun des côtés. Le quadrilatère formé avec les centres de ces quatre carrés est lui même un carré. Théorème de Thébault (1882-1960)

Parallélogramme et triangle rectangle
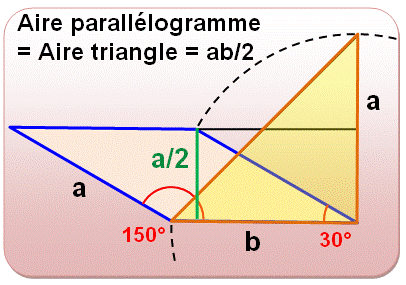
Un triangle rectangle de côté a et b quelconques. Un parallèlogramme de côté a et b et avec un angle de 30°. Le sinus de l'angle 30° est égal à 1/2. La hauteur (en vert) du paralllélogramme est égale à: a/2. Son aire vaut: a/2 x b = 1/2 ab Alors que celle du triangle rectangle vaut 1/2 ab, également.

Voir Démonstration du théorème de Pythagore avec des triangles

Partage du parallélogramme

Comment partager un parallélogramme en triangles dont les aires soient dans les rapports: 1, 2, 3 et 4?

Parallélogramme ABCD.

Points milieux: I et J.

Les triangles AMI et IMB ont même hauteur (h, non représentée) et même longueur de base (AI = IB): ils ont la même aire, notée "a".

Même chose pour BMJ et JMC, dont l'aire est notée "b".

Les triangles CBI et CDJ ont une aire égale au quart de celle du parallélogramme; à partir de là, on calcule les aires indiquées sur la figure (ci-contre).

Calcul des aires indiquées sur la figure

Aire (CDJ) = Aire(CBI) = a + 2b

Aire (ABCD) = 4(a + 2b)

Aire(CDM) = a + b

Aire(ADM) = Aire(ABCD) – (2a + 2b + a + b) = 4(a + 2b) – (3a + 3b) = a + 5b

Quelle est la relation entre les aires a et b?

Aire(MAB) + Aire(MCD) = ½ (AB.h1 + CD.h2) = ½ (AB.h) = ½ Aire(ABCD) (hauteur non représentée).

Aire(MAD) + Aire(MBC) = ½ aire (ABCD) par le même raisonnement.

Bilan: (2a + a + b) = (a + 5b + 2 b) = 2(a + 2b)

3a + b = a + 7b = 2a + 4b

a = 3b

Aires des quatres triangles:

Triangle	MBC	MCD	MAB	MAD
Aire	2b	3b+ b = 4b	2a = 6b	a + 5b = 8b
Rapport	1	2	3	4

Voir Partage du triangle en sept

Les deux parallélogrammes ABCD et ABEC ont même aire, disons 4. Dans ces deux parallélogrammes les petits triangles ont même aire e = f = b + c = a + d = ¼ x 4 = 1 g = h = a + c = b + d = ¼ x 4 = 1

123, curiosité avec deux parallélogrammes Les surfaces ainsi formées sont dans le rapport 1 pour a et b 2 pour c et d 3 pour e, f, g et h

Dans le triangle ABC: O est le milieu de AC, et BO est médiane de ABC. O' est le milieu de BC, AO' est médiane de ABC. Les médianes se coupent au centre de gravité M situé au 2/3 de chaque médiane en partant du sommet BM = 2 MO et AM = 2 MO' Dans un triangle, une droite issue d'un sommet et coupant le côté opposé dans un certain rapport r, le rapport des aires des sous triangles formés par cette droite est dans le même rapport r Dans ABO' => c = 2a Dans ABO => c = 2b Or, b + c = 1 => a = 1/3 et c = 2/3 En recoupant toutes ces informations e = f =g = h = 1 c = d = 2/3 a = b = 1/3

D'après une idée de Élisabeth Busser et Gilles Cohen – Le Monde 28 février 2006

Niveau avancé**

Aire du parallélogramme – Analytique
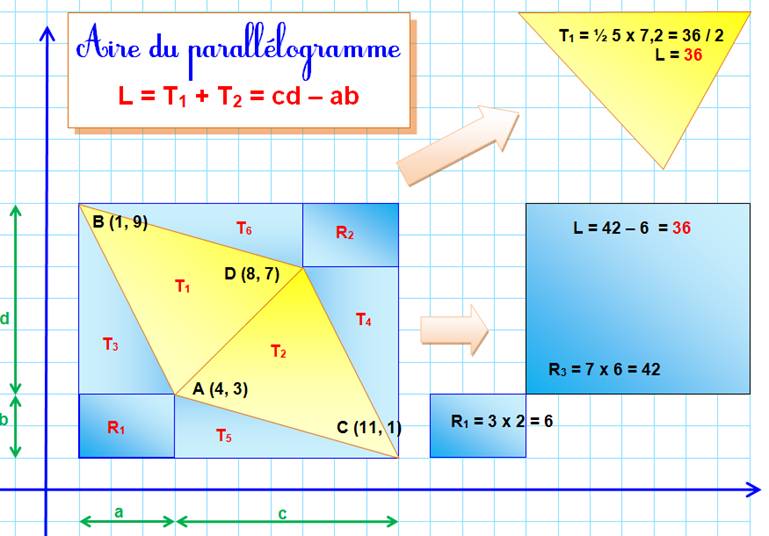
Comment calculer l'aire du parallélogramme en connaissant les coordonnées de trois points (A, B et C); ou de deux vecteurs (Ab et AC). Figure Calcul
Nous cherchons l'aire du parallélogramme (jaune)	L = T1 + T2
Elle est égale à celle du grand rectangle diminuée des parties bleues	L = R – (R1 + R2 + T3 + T4 + T5 + T6) = R – 2(R1 + T3 + T5)
En développant	L = (a + c)(b + d) – 2(ab + ad/2 + cb/2)
En calculant	L = ab + ad + bc+ cd – 2ab – ad – bc
Bilan	L = cd – ab
En coordonnées (Barres verticales = prendre la valeur absolue)
En vecteurs
Avec pour les trois points déterminant le parallélogramme
Vérification (voir figure)	A (4, 3) , B (1, 9) , C(11, 1) L = (11 – 4) (9 – 3) – (1 – 4)(1 – 3) = 7 x 6 – (-3)(-2) = 42 – 6 = 36

Voir Aire du triangle / Volume du parallélépipède

Diagonales et milieu – Démonstration
Diagonales
Position du point M par deux voies
En égalant

Retour	Quadrilatère
Suite	Parallélogramme – Carré magique 3x3 Parallélogramme – Constructions élémentaires Parallélogramme – Dans le cube Parallélogramme – Exercice sur les angles Parallélogramme – Formules Parallélogramme – Partagé avec les points milieux Parallélogramme divisé Parallélogramme et octogone Parallélogramme et triangle équilatéral Parallélogramme et parallèles aux côtés Pavé ou parallélépipède Quizz géométrie – Illustration Règle du parallélogramme (vecteurs) Théorème de Pappus-Clairaut
Voir	4 Couleurs Carré dans le triangle Constructions avec des allumettes Géométrie – Index Hexagones Jeux – Index Nombres Carrés Pavage du carré Pentagones Polygones Rectangle Somme de vecteurs Triangles
DicoNombre	Nombre 4
Sites	Parallélogramme - Wikipédia Parallelogram (Mathworld) – toutes les formules utiles Thébault problem – avec animation de A. Bogomolny Interactive parallelogram Parallelogram – Wolfram
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/QuadPara.htm