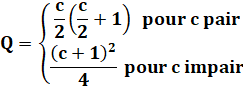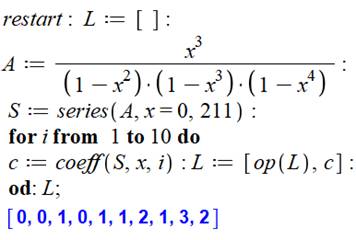|
Édition du: 11/03/2024 |
|
INDEX |
Triangles entiers |
|||
![]()
|
Triangles
ENTIERS spécifiques
Quels
sont les triangles dont la longueur des côtés est un nombre entier ? Le
périmètre
est évidemment un nombre entier. D'autres
éléments peuvent aussi être mesurés en nombres entiers. Par exemple, si l'aire
est un nombre entier, le triangle est héronien. Il existe
donc plusieurs types
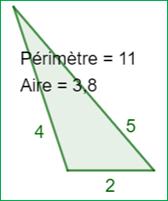
de triangles entiers: avec aire entière, en duo avec la même aire entière, … La figure
montre un triangle entier (2, 4, 5), un des quatre tels triangles avec un
périmètre égal à 11. Le seul avec des nombres distincts. |
||
|
|
Sommaire de cette page >>> Types de triangles entiers >>> Triangles entiers >>> Quantité de triangles entiers et périmètre >>> Quantité de triangles entiers et côtés >>> Hauteurs et médianes des triangles entiers >>> Triangles entiers jusqu'à un périmètre égal à 8 >>> Programmation >>> En duo et plus >>> Triangles entiers à hauteur entière |
Débutants Glossaire |
|
Entier quelconque Entier primitif |
Côtés entiers. >>> Côtés entiers et premiers entre eux. |
|
|
Entier rationnel |
Cotés rationnels, ou Rapport rationnel entre côtés, ou Cotés rationnels et angles en degrés
rationnels. |
|
|
Irrationnel |
Un côté au moins est irrationnel. |
|
|
Entier avec périmètre
imposé |
Tous les triplets, partitions de P,
satisfaisant l'inégalité triangulaire. |
|
|
Entier médian |
Avec médianes entières – Héronien ou
non. |
|
|
Entier auto-médian |
Les médianes
sont dans les mêmes rapports que les côtés. |
|
|
Équilatéral à
distances entières |
Triangle
équilatéral tel qu'il existe un point à distances entières des sommets. >>> |
|
|
Héronien |
Triangle entier avec une aire en
nombre entier. >>> |
|
|
Pythagore |
Triangle rectangle entier; il est
aussi héronien. La hauteur de l'hypoténuse n'est
jamais un entier. >>> |
|
|
Héronien a progression
arithmétique, et autres |
Les longueurs des côtés sont en progression
arithmétique. D'autres types de triangles
héroniens peuvent être investigués: angles doubles, périmètre quatre fois un
nombre premier, etc. |
|
|
Fibonacci |
Héronien avec des nombres de
Fibonacci pour côtés. Un seul triangle de Fibonacci est connu. >>> |
|
|
Entiers en duo |
Deux (ou plus) triangles entiers
partageant deux côtés de mêmes longueurs. >>> |
|
|
Spéciaux |
Angles rationnels et côtés
rationnels ou quadratiques >>> |
|
L'imagination est au pouvoir … Voir Intégrer triangles
![]()
|
Triangles entiers Un triangle dont les longueurs des
côtés sont des nombres entiers. Il existe une infinité de triangles entiers
en multipliant toutes les longueurs par k. Suite Triangles entiers Triangles rationnels Un triangle dont les longueurs des
côtés sont des nombres rationnels (des fractions). Il suffit de multiplier les longueurs
par le plus petit
commun multiple des dénominateurs pour retrouver un triangle entier.
|
Exemples de triangles
entiers
|
|||
Anglais: Integer triangle or integral triangle
|
Existence Tout triplet de nombres entiers est
susceptible de représenter un triangle entier dès que l'inégalité
triangulaire est satisfaite: a + b > c avec a et b les deux plus
petits côtés. Un tel triangle est unique ou
primitif, hors similitudes (k fois les côtés). |
Exemple avec un
périmètre égal à 7 Il existe quatre possibilités
d'atteindre 7 avec la somme de trois nombres entiers: 7 = 2 + 2 + 3; 2 + 2 > 3; OUI 7 = 1 + 3 + 3; 1 + 3 > 3; OUI 7 = 1 + 2 + 4; 1 + 2 < 4; NON 7 = 1 + 1 + 5; 1 + 1 < 5; NON Seules les deux premières satisfont
l'inégalité triangulaire. Alors, il n'existe que deux triangles entiers de
périmètre 7.
|
||
|
Quantités Étant donné un périmètre P, toutes
les tripartitions (a,
b, c) de P avec a + b > c forment des triangles entiers. La quantité de tels triangles selon
le périmètre est donnée par le polynôme générateur d'Alcuin. Le coefficient de x7 est
2, montrant qu'il existe deux triangles entiers de périmètre 7. La liste montre qu'il existe huit
triangles entiers pour un périmètre de 20.
|
Polynôme générateur Formule d'Alcuin
(735-804)
Voir Polynôme
générateur Liste: quantité de
triangles entiers pout P de 1 à 20 0, 0, 1, 0, 1, 1, 2, 1, 3, 2, 4, 3,
5, 4, 7, 5, 8, 7, 10, 8 |
||
|
Quantité selon
périmètre |
Q = Proche entier de (p² / 48) pour
p pair Q = Proche entier de ((p²+3) / 48)
pour p impair |
||
|
Triangle entiers
distincts La même formule avec un décalage de 6
indique la quantité de triangles entiers dont les longueurs des côtes sont
des entiers distincts. Le coefficient de x3 est
1, montrant qu'il existe un triangle entier de périmètre 3 + 6 = 9 avec des
côtés distincts (2, 3, 4). |
Condition
|
||
|
Quantité selon
longueur des côtés |
C'est la quantité de triangles
entiers primitifs pour des côtés de longueur maximale
d. |
|
|
Selon la longueur du
grand côté Le côté qui mesure c étant le plus
long, la quantité de triangles entiers tels que: |
Q = {1, 2, 4, 6, 9, 12, 16, 20, 25,
30, 36, 42, 49, 56, 64, 72, 81, 90 …} |
|
|
Dans le demi-cercle de
diamètre c Dans ce cas:
|
Q = { 1, 2, 3, 5, 6, 8, 11, 13, 15, 17,
21, 25, 27, 31, 34, 39, 43, 48, 52 .. } |
|
|
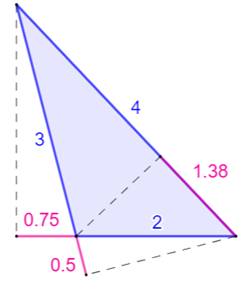
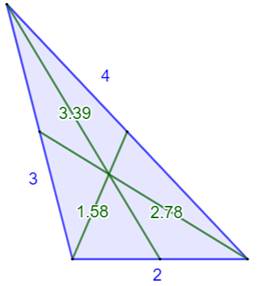
Les hauteurs d'un triangle entier découpe
les côtés (ou leur prolongement) en segments de longueur rationnelle. Sur cette figure:
|
|
|
|
La longueur d'une médiane est donné par:
Ce qui veut dire que: Sur cette figure: a = 2, b = 3 et c
= 4.
|
|
|
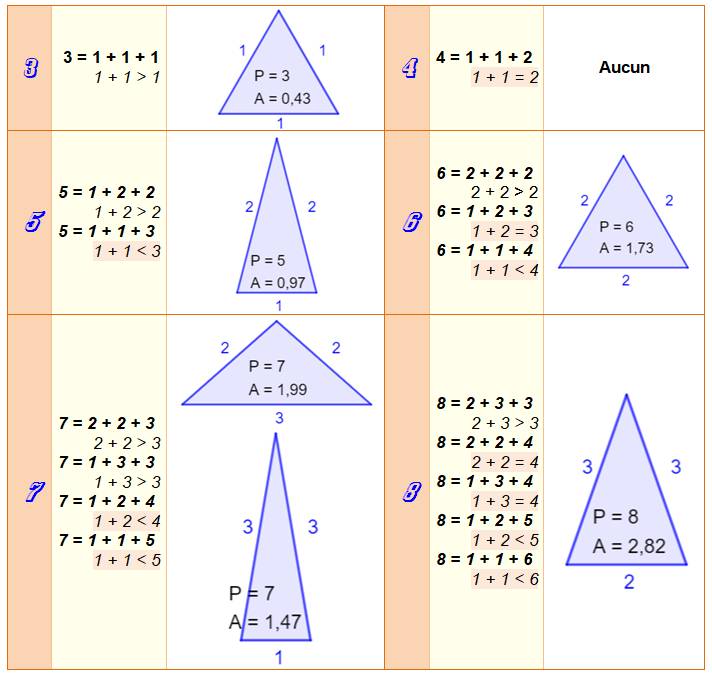
Triangles entiers jusqu'à un périmètre égal à 8
Ils
sont tous isocèles.
Suite Table
des triangles entiers (pdf)
Cas
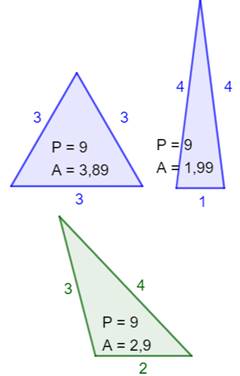
du périmètre 9
|
Pour le nombre 9, trois tripartitions recevables existent,
soit trois triangles entiers de périmètre 9.
|
|
Voir Brève
766
|
Programme Maple
|
But Utiliser le polynôme générateur et
en extraire les coefficients qui représentent la quantité de triangles
entiers pour un périmètre donné. Commentaires Initialisation générale et ouverture
d'une liste vide (L). Définition du polynôme générateur. Calcul de sa division (séries en x
pour 10 termes). Extraction des coefficients et stockage dans la liste L. Impression de la liste. |
|
Voir Programmation – Index
|
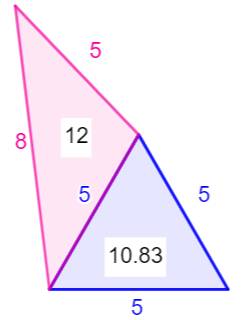
Deux triangles qui partagent deux
dimensions:
|
|
|
|
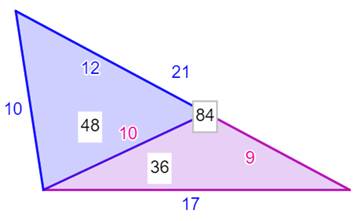
Deux triangles qui partagent deux
dimensions:
|
|
|
|
Deux triangles héroniens qui
partagent deux dimensions:
|
|
|
|
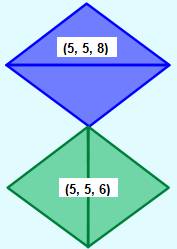
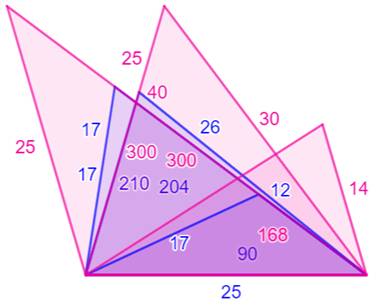
Un jeu de six triangles héroniens
ayant au moins une dimension commune: En bleu:
En rose:
|
|
|
|
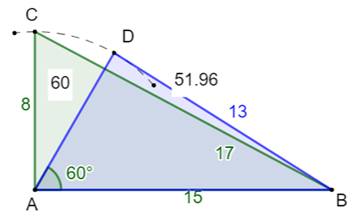
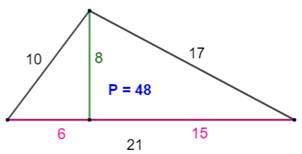
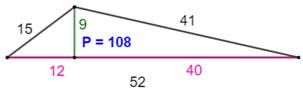
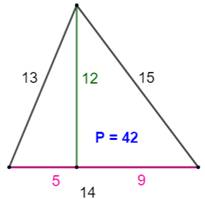
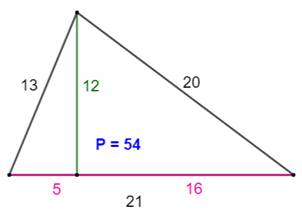
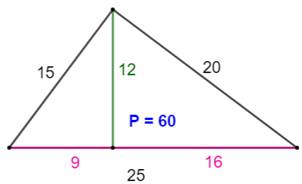
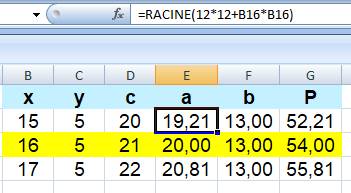
Les plus petits triangles quelconques
avec trois côtés et une hauteur en nombres entiers. P est le périmètre. |
|
||
|
Ces configurations sont obtenues par
recherche manuelle ou avec tableur ou
avec un programme. Il suffit de prendre x et y
(segments découpés sur le côté c avec
la hauteur) et de calculer a et b (autre côtés) avec le théorème
de Pythagore. |
|
||
|
Listes des plus petits
triangles avec h, x, y, c, a, c, P (en rose les exemples vus ci-dessus) |
|||
|
8, 6, 15, 21, 10, 17, 48 9, 12, 40, 52, 15, 41, 108 12, 5, 9, 14, 13, 15, 42 12, 5, 16, 21, 13, 20, 54 12, 5, 35, 40, 13, 37, 90 12, 9, 16, 25, 15, 20, 60 12, 9, 35, 44, 15, 37, 96 12, 16, 35, 51, 20, 37, 108 15, 8, 20, 28, 17, 25, 70 15, 8, 36, 44, 17, 39, 100 15, 20, 36, 56, 25, 39, 120 16, 12, 30, 42, 20, 34, 96 16, 12, 63, 75, 20, 65, 160 16, 30, 63, 93, 34, 65, 192 18, 24, 80, 104, 30, 82, 216 20, 15, 21, 36, 25, 29, 90 20, 15, 48, 63, 25, 52, 140 20, 15, 99, 114, 25, 101, 240 20, 21, 48, 69, 29, 52, 150 20, 21, 99, 120, 29, 101, 250 20, 48, 99, 147, 52, 101, 300 |
21, 20, 28, 48, 29, 35, 112 21, 20, 72, 92, 29, 75, 196 21, 28, 72, 100, 35, 75, 210 24, 7, 10, 17, 25, 26, 68 24, 7, 18, 25, 25, 30, 80 24, 7, 32, 39, 25, 40, 104 24, 7, 45, 52, 25, 51, 128 24, 7, 70, 77, 25, 74, 176 24, 10, 18, 28, 26, 30, 84 24, 10, 32, 42, 26, 40, 108 24, 10, 45, 55, 26, 51, 132 24, 10, 70, 80, 26, 74, 180 24, 18, 32, 50, 30, 40, 120 24, 18, 45, 63, 30, 51, 144 24, 18, 70, 88, 30, 74, 192 24, 32, 45, 77, 40, 51, 168 24, 32, 70, 102, 40, 74, 216 24, 45, 70, 115, 51, 74, 240 28, 21, 45, 66, 35, 53, 154 28, 21, 96, 117, 35, 100, 252 28, 45, 96, 141, 53, 100, 294 |
30, 16, 40, 56, 34, 50, 140 30, 16, 72, 88, 34, 78, 200 30, 40, 72, 112, 50, 78, 240 32, 24, 60, 84, 40, 68, 192 33, 44, 56, 100, 55, 65, 220 35, 12, 84, 96, 37, 91, 224 36, 15, 27, 42, 39, 45, 126 36, 15, 48, 63, 39, 60, 162 36, 15, 77, 92, 39, 85, 216 36, 27, 48, 75, 45, 60, 180 36, 27, 77, 104, 45, 85, 234 36, 48, 77, 125, 60, 85, 270 39, 52, 80, 132, 65, 89, 286 40, 9, 30, 39, 41, 50, 130 40, 9, 42, 51, 41, 58, 150 40, 9, 75, 84, 41, 85, 210 40, 9, 96, 105, 41, 104, 250 40, 30, 42, 72, 50, 58, 180 40, 30, 75, 105, 50, 85, 240 40, 30, 96, 126, 50, 104, 280 40, 42, 75, 117, 58, 85, 260 |
40, 42, 96, 138, 58, 104, 300 40, 75, 96, 171, 85, 104, 360 42, 40, 56, 96, 58, 70, 224 45, 24, 28, 52, 51, 53, 156 45, 24, 60, 84, 51, 75, 210 45, 28, 60, 88, 53, 75, 216 48, 14, 20, 34, 50, 52, 136 48, 14, 36, 50, 50, 60, 160 48, 14, 55, 69, 50, 73, 192 48, 14, 64, 78, 50, 80, 208 48, 14, 90, 104, 50, 102, 256 48, 20, 36, 56, 52, 60, 168 48, 20, 55, 75, 52, 73, 200 48, 20, 64, 84, 52, 80, 216 48, 20, 90, 110, 52, 102, 264 48, 36, 55, 91, 60, 73, 224 48, 36, 64, 100, 60, 80, 240 48, 36, 90, 126, 60, 102, 288 48, 55, 64, 119, 73, 80, 272 48, 55, 90, 145, 73, 102, 320 48, 64, 90, 154, 80, 102, 336 |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/TriaEnti.htm
|