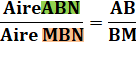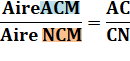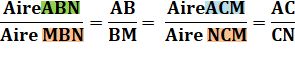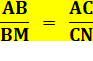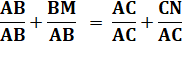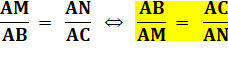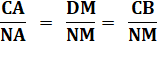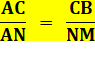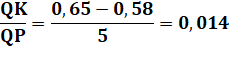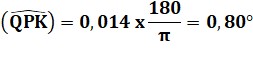NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/11/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Base de la Géométrie
Débutants Général	Théorèmes INCONTOURNABLES			Glossaire Géométrie
INDEX BASES GÉOMÉTRIE	Pythagore	Thalès	Thalès Applications
	Troisième	Sommaire de cette page >>> Approche >>> Étoiles qui grossissent >>> Triangles rectangles emboités >>> Théorème de Thalès >>> Démonstration >>> La hauteur de l'immeuble >>> Les phares de la voiture

THÉORÈME DE THALÈS Explications pour débutants. Une affaire de proportions, de similitudes, qui se conservent lors de certaines transformations ou que l'on observe dans les triangles. Le théorème de Thalès est un outil qui permet de calculer la longueur de certains segments.

Anglais: Intercept theorem / Side splitter theorem / Thales' theorem / Basic proportionality theorem

Voir Thalès de Milet / Impératif (cf. ne tire pas sans s à tire)

En bref

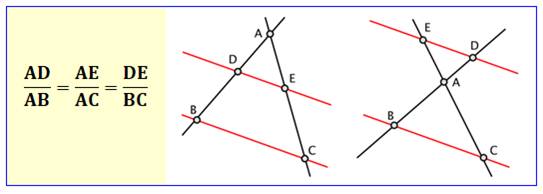
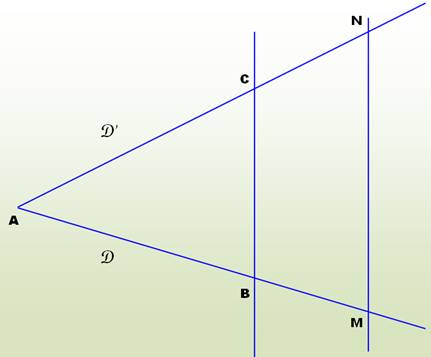
Soit un triangle ABC, et deux points D et E des droites (AB) et (AC) de sorte que la droite (DE) soit parallèle à la droite (BC). Alors on a :

Approche
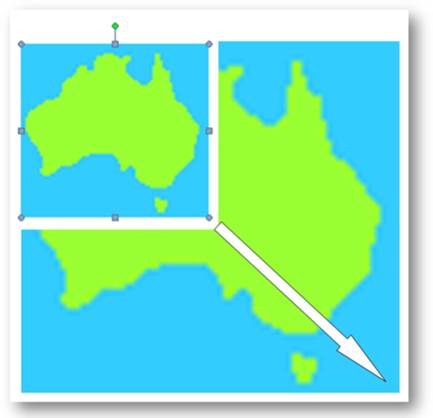
Une loupe qui vous fait voir un objet plus gros vous montre ce qu'est le théorème de Thales, sans que vous vous en rendiez compte. Lorsque sur l'ordinateur vous tirez une image (ici, les contours de l'Australie) par son ancre dans le coin, vous agrandissez cette image sans la déformer; c'est encore du Thalès. Agrandir ou réduire un objet en conservant ses proportions, c'est appliquer le théorème de Thalès.

Les étoiles qui grossissent

Les six étoiles de ce dessin sont toutes semblables Elles sont obtenues à partir de la plus petite en grossissant 2 fois, 3 fois … Je remarque que: les angles des branches des étoiles sont conservés (36°). comparée à l'étoile 1, la branche de l'étoile 3 est trois fois plus grande; et celle de l'étoile 6 est six fois plus grande. comparée à l'étoile 3, la branche de l'étoile 6 est deux fois plus grande. etc. 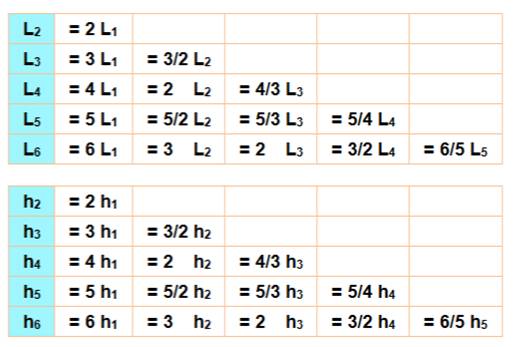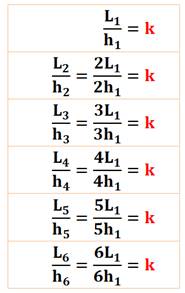Les angles sont conservés et les dimensions sont augmentées dans les mêmes proportions, dans le même rapport. Je remarque aussi que: les étoiles s'inscrivent dans un triangle (rose). les centres sont sur une droite. cette droite des centres, la droite horizontale et toutes les droites verticales passant par les centres forment une série de triangles rectangles ayant un angle commun (la pointe à gauche).

Les triangles rectangles emboités
Notons hi la hauteur des triangles rectangles et Li la longueur du côté horizontal.
Nous avons observé que les dimensions étaient augmentées par 2, 3, … Ce qui se traduit par ce tableau: Comparons les dimensions en divisant L par h. Pour chacun des triangles le rapport des longueurs des côtés sont conservés (k).

Théorème de Thalès
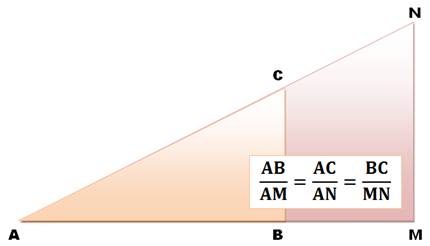
Simple: triangles rectangles Deux droites sécantes (AM et AN); deux perpendiculaires (BC et MN); la figure forment deux triangles rectangles emboités (ABC et AMN).
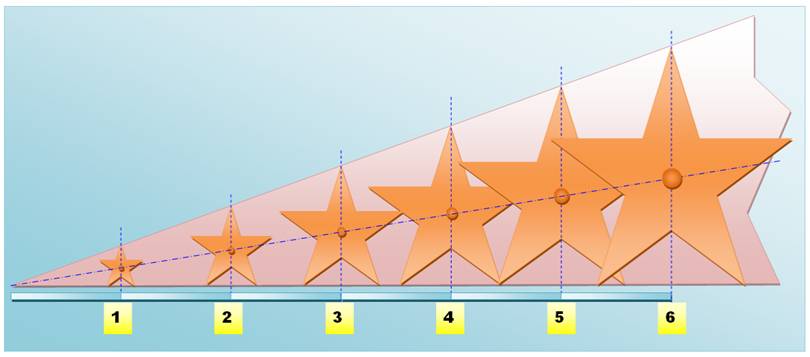
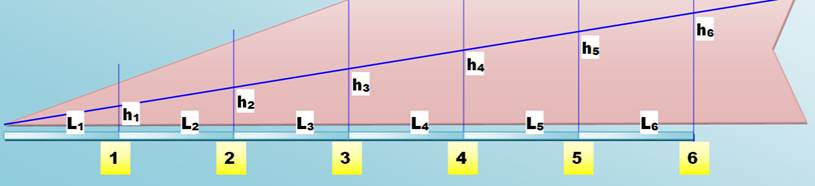
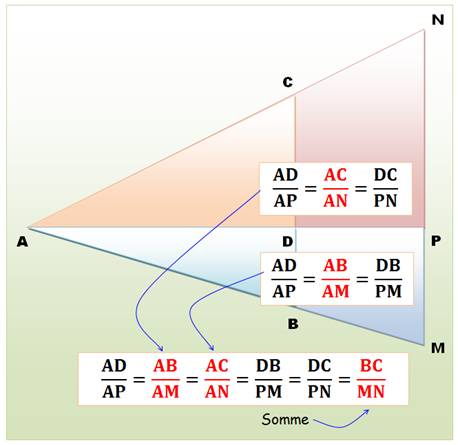
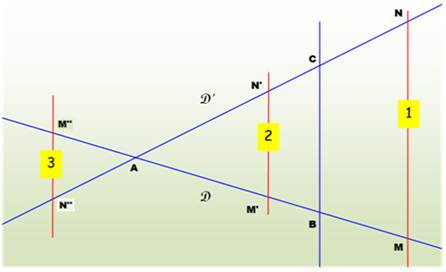
Vers le cas général: association de triangles rectangles Deux triangles emboités dupliqués et accolés. Les triangles ABC et AMN sont alors deux triangles quelconques emboités. Une particularité: BC et MN sont parallèles car perpendiculaires a AP en D et P.
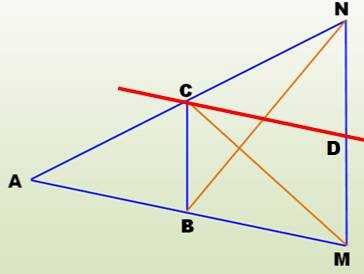
Le théorème de Thalès Deux droites et sécantes en A. Deux points distincts B et M sur la droite . Deux points distincts C et N sur la droite . Si Les droites (BC) et (MN) sont parallèles alors: Attention de toujours prendre ces rapports en partant du sommet commun A.
Le théorème est vrai quelles que soient les positions des points M et N par rapport à A: Cas 1), 2) ou 3) de la figure. La réciproque dit que, si l'on est en présence d'une telle proportion, les droites BC et MN sont parallèles.

Démonstrations
Mêmes débutants, ne nous privons pas de la démonstration simple et amusante. Deux jolis théorèmes sur les triangles quelconques vont être utiles.
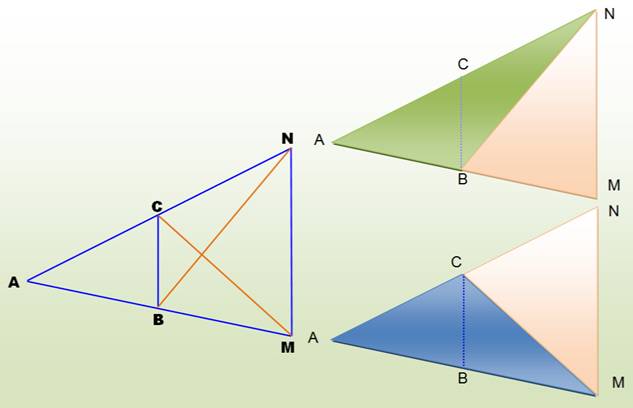
Découpons notre figure de deux manières différentes (les deux vues à droite).		Triangles: ABN et NBM Triangles: ACM et CMN
Les deux triangles roses NBM et CMN, ayant un côté commun et le sommet opposé sur une parallèle au côté commun ont la même aire. En retirant des aires égales du triangle ABC, on obtient des triangles de mêmes aires.		Aire NBM = Aire CMN Aire ABN = Aire ACM Les triangles de couleurs sont de même aire deux à deux.
La droite BN partage le triangle AMN en deux triangles d'aires proportionnelles. Idem pour la droite CM.
En rapprochant ces égalités, car les aires des triangles sont égales deux à deux. Cette proportion finale entre longueurs reflète bien le théorème de Thalès.

Cherchons à passer à la forme classique.
Ajoutons 1 de chaque côté de l'égalité, sous la forme d'une fraction unitaire.
Nous retrouvons la forme classique du théorème de Thalès.

Démontrer la 3^e relation avec BC et MN passe par le tracé de la parallèle montrée en rouge. Alors dans le parallélogramme BCDM DM = CB Avec la première proportion (vue ci-dessus) et avec S pour sommet: Où en remettant en forme, avec A pour sommet:

Merci à Jean-Marc Detourmignies pour sa relecture attentive et ses suggestions

La hauteur de l'immeuble
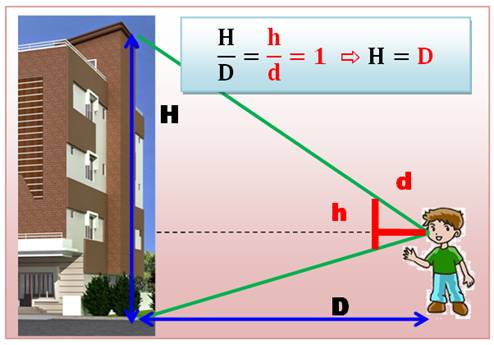
Prenez deux morceaux de bois de même longueur (h = d) et formez un T (non symétrique) avec ces deux morceaux (rouge). Alignez votre œil avec, d'une part, le haut du T et le haut de l'immeuble et, d'autre part, le bas du T et le bas de l'immeuble (traits verts). Il faut, pour cela, ajuster le T et ajuster la distance de l'observateur. Mesurez la distance D au sol. C'est également la hauteur de l'immeuble. Voir théorème de Thalès, association des triangles rectangles

Voir Hauteur de la pyramide / Corde du jardinier

Les phares de la voiture
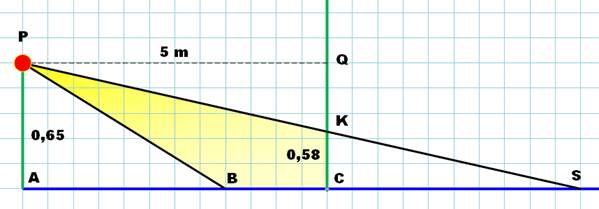
Le phare de la voiture (P) éclaire un mur (QC).
Éclairage conforme?	L'éclairage est conforme si l'inclinaison du faisceau QK / QP est compris entre 0,01 et 0,015. Est-ce le cas? Conforme.
Mesure de l'angle QPK?	Ce calcul se fait en utilisant la tangente de l'angle: Passage des radians aux degrés
Distance d'éclairage AS? (Si pas de mur)	Thalès va entrer en ligne … Les deux triangles à considérer: KQP et KCS. Cotés alignés: PKS d'une part et QKC d'autre part; Côtés parallèles: PQ et CS; Tous les angles sont égaux deux à deux. Ces deux triangles sont semblables. AS =AC+CS = 5 + 41,42 = 46,42 m

Cette question comptait pour 6 points sur 40 au Brevet de 2014

Suite	Théorème de Thalès en action Théorème de la bissectrice Énigme de la hauteur Transformations Droites Similitudes Triangles
Voir	Anamorphoses Formulaire périmètres, aires, volumes Fractales Géométrie – Index Géométrie – Vue d'ensemble Homothétie – Débutant Mathématiques Transformation du boulanger
Aussi	DicoMot DicoNombre Théorie des nombres – Index Jeux, énigmes – Index Humour et pensées – Index
Site	Démonstration du théorème de Thales (pdf) Théorème de Thalès – Wikipédia
Cette page	http://villemin.gerard.free.fr/GeomLAV/Bases/Thales.htm