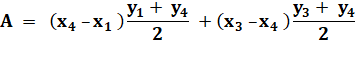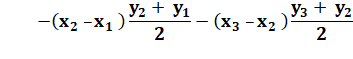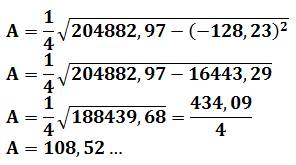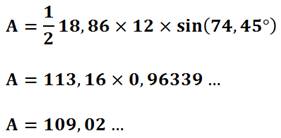|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
AIRE du QUADRILATÈRE quelconque La donnée
des quatre côtes d'un quadrilatère
ne suffit pas pour
caractériser un quadrilatère, ni pour calculer son aire. D'autres
connaissances sont nécessaires: longueur des diagonales, valeur des angles,
ou coordonnées des sommets. L'aire du quadrilatère peut
être estimée ou calculée de diverses manières:
|
Anglais: Quadrilateral area
|
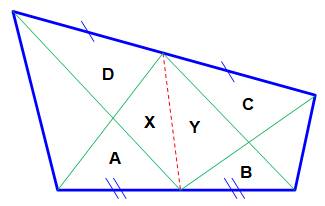
Construction Un
quadrilatère et une médiane (pointillé rouge) Aires
des triangles notées: A, B, C, D, X et Y. Quelle
est l'aire de A connaissant B, C et D ? Piste La
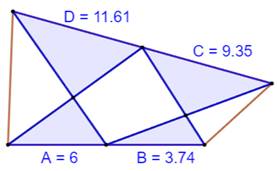
médiane d'un triangle le partage en deux triangles de même aire. Soustraction Exemple A
= 3,74 – 9,35 + 11,61 = 6 |
|
|
Voir Brève 55-1084
|
|
||
|
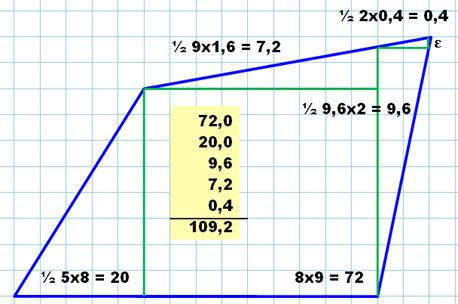
Méthode de découpe selon le
quadrillage
|
Aire =
somme des aires des triangles rectangles |
|
|
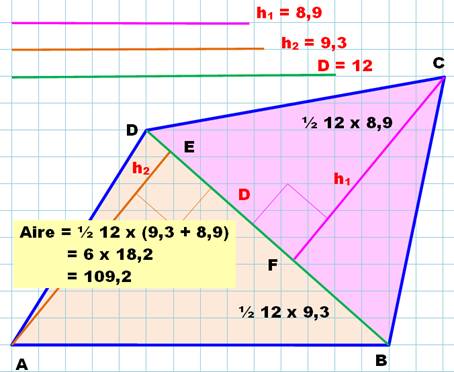
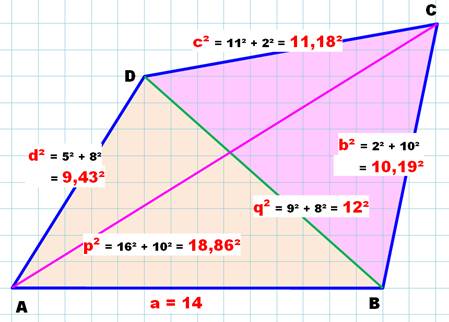
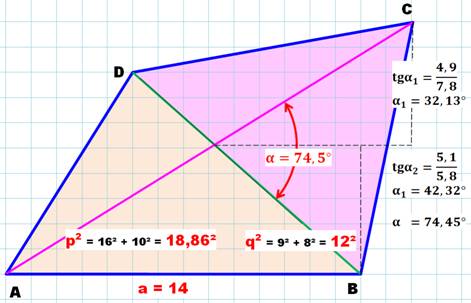
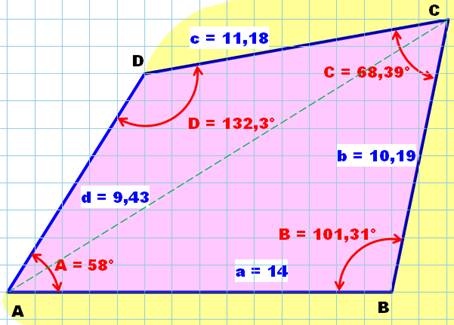
Méthode de découpe selon une
diagonale
|
Aire = ½ D (h1 + h2) Notez que la longueur de la diagonale D se calcule aussi via Pythagore:9² + 8² = 144 = 12² |
|
|
|
|||
|
|
|
||
|
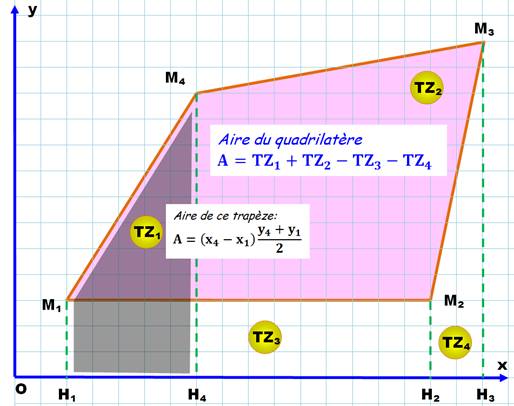
Rappel: aire du trapèze |
Produit de la hauteur par la demi-somme des bases. >>> |
||
|
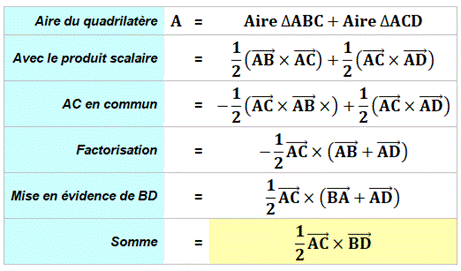
Formulation analytique de l'aire
du quadrilatère CONVEXE Pour les quadrilatères
concaves, il est conseillé de reprendre le calcul dès le départ, avec les
trapèzes. |
Barres verticales = prendre la valeur absolue (sans
signe) |
||
|
Application numérique |
|
||
|
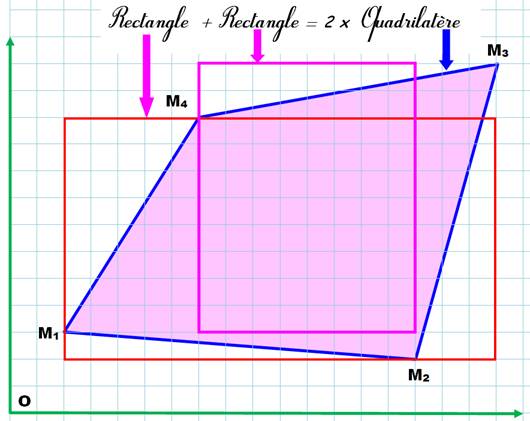
Interprétation géométrique La formule est la somme de deux produits dont chacun est l'aire d'un
rectangle. Le recouvrement des deux rectangles sur deux fois le quadrilatère est
une dissection faisable mais pas simple. |
|
||
Suite Aires des quadrilatères formés
par les bi-médianes avec énigmes de la quatrième parcelle
|
|
||
|
|
|
|
|
|
|||
|
|
|
||
|
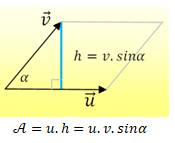
Justification avec les vecteurs Le produit
scalaire est l'aire du paralléogramme formé par deux vecteurs. Soit la
moitié pour l'aire du traingle. Rappel
|
|
||
|
|
||
|
Application numérique
|
Ou, sous forme développée:
|
|
|
Formule de Brahmagupta pour les quadrilatères
inscriptibles. Voir Démonstration
/ pour les triangles Voir Quadrilatère
inscriptibles |
Si
la quadrilatère est inscriptible dans un
cercle de rayon R, alors A + B = 180°, et le cosinus de sa moitié est nul. La
formule devient:
Et avec le rayon du cercle:
Propriété: l'aire du
quadrilatère inscrit occupe la surface maximale pour des longueurs de côtés
données. Relation entre diagonales et côtés pour un quadrilatère inscriptible: p.q = a.c + b.d |
|
|
Formule pour tout quadrilatère |
|
|
|
|
||
|
|
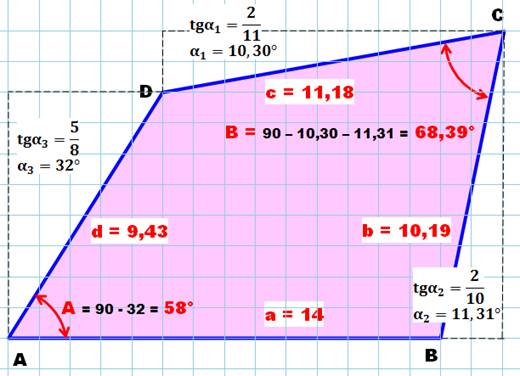
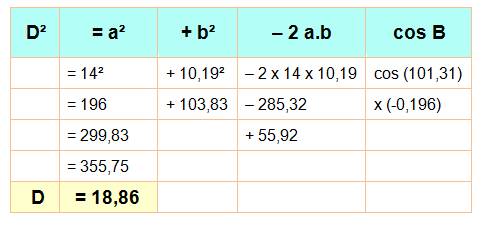
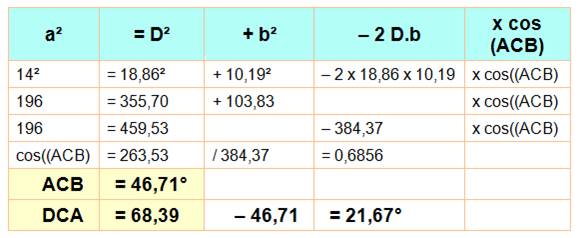
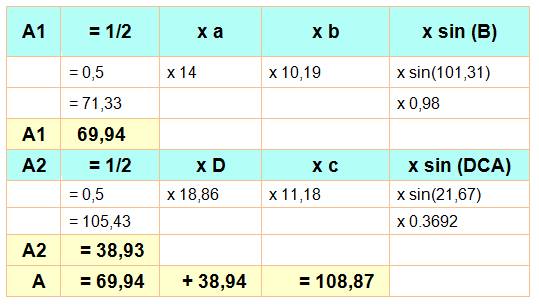
Seuls a, b, c, B et C (en jaune) sont connus. Aire Quadrilatère = Aire triangle ABC + Aire
triangle ACD |
|
|
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()