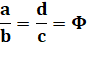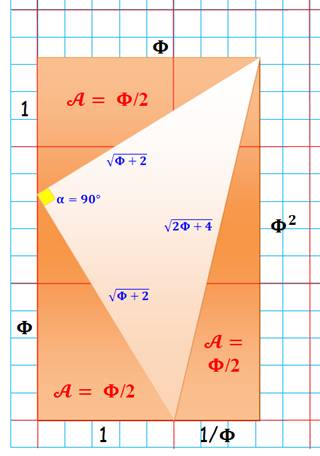
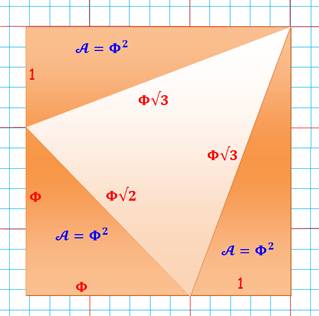
NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 13/10/2010

Orientation générale        DicoMot Math          Atlas                   Références                     M'écrire

Barre de recherche          DicoCulture              Index alphabétique                               

    

Débutants

NOMBRE D'OR

Nombres

Glossaire

NOMBRE D'OR

 

NOMBRE D'OR

Géométrie

 

Index

Introduction

Proportion

Construction

Géométrie

Étoile

Aire Phi

Cercle

 

Sommaire de cette page

>>> Triangle et rectangle en or

>>> Évaluation des rapports

>>> Cas possibles

>>> Cas typiques

 

 

 

Triangles d'aire Phi dans rectangle

 

 

 

Triangle et rectangle en or

 

*      Un triangle inscrit dans un rectangle forme un triangle central et trois triangles externes dont l'aire est identique.

 

*      Alors les deux côtés découpés du rectangle sont en section dorée.

 

*      Cette figure repose sur les égalités suivantes:

 

 

 

 

*      De sorte que le produit des côtés pour les trois triangles est égal à Phi (et l'aire du triangle à Phi/2).

*      Le triangle central est isocèle et rectangle.

Rappel: 1/Phi   = 0,618

                Phi   = 1,618… et

                Phi² = 2,618…

 

 

 

Évaluation des rapports

 

*      Rectangle ABCD.

 

*      Les trois triangles

*  APQ,

*  PBC et

*  CDQ

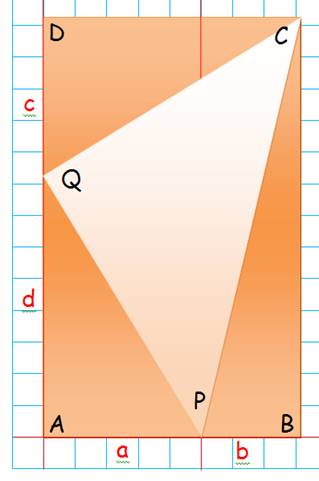
doivent avoir la même aire.

 

*      Quelles sont les relations

*  entre a et b,

*  de même que, entre c et d ?

 

*      On rappelle que dans un triangle rectangle l'aire est égale au demi-produit des côtés adjacents à l'angle droit.

 

*      Égalité des aires.
En développant et en multipliant tout par 2.

(a + b) c/2 = ad /2 = b (c + d) /2

ac + bc  = ad = bc + bd

*      Avec le "bc" commun on déduit l'égalité ci-contre.
Notez la même proportion entre a b et c d.

ac  = bd

c    = bd / a

b/a = c/d

*      On remplace c par sa valeur dans une des égalités du dessus.

*      On simplifie par d et on divise par a (qui est une longueur non nulle).

ad = ac + bc

     = a (bd/a) + b (bd/a)

     = abd /a + b²d / a

a   = ab /a + b²/ a

1   = b / a + b² / a²

*      En posant: – b/a = x

On obtient l'équation d'or dont on connaît les deux solutions.
Seule qui donne c/d positif est retenue.

x² - x - 1 = 0

x1 = 1,618… et x2 = - 0,618…

b/a = 0,618…

c/d = 0,618…

*      Une telle figure impose que les côtés coupés du rectangle le soit en section dorée.

 

 

Cas possibles

 

*      Les deux rapports valent Phi, mais nous avons la liberté sur deux variables.

*      Explorons diverses possibilités:

(1)

a

b

c

d

a/b

d/c

A1

A2

A3

e

f

g

(2)

1

0,618

1

1,618

1,618

1,618

1,618

1,618

1,618

1,902

2,690

1,902

(3)

2

1,236

1

1,618

1,618

1,618

3,236

3,236

3,236

3,387

2,895

2,573

(4)

3

1,854

1

1,618

1,618

1,618

4,854

4,854

4,854

4,956

3,208

3,409

(5)

1

0,618

2

3,236

1,618

1,618

3,236

3,236

3,236

2,573

5,272

3,387

(6)

1

0,618

0,618

1

1,618

1,618

1,000

1,000

1,000

1,732

1,732

1,414

(7)

1,618

1

1

1,618

1,618

1,618

2,618

2,618

2,618

2,803

2,803

2,288

 

*      En ligne (1), on donne abcd selon les notations de la figure du haut; les deux rapports que nous cherchons à égaler au nombre d'or; les aires des trois triangles; on ajoute la mesure des côtés du triangle interne (efg).

*      En ligne (2), on retrouve la figure de tête avec a  = 1, b = 1/Phi = 0,618…, c= 1 et d= Phi = 1,618.

*      En lignes (3) à (5), on montre que l'on peut multiplier a et b par un nombre et c et d par le même ou un autre; dans tous les cas la propriété de la figure est conservée: les trois triangles ont même aire. Il y a donc une infinité de cas possibles.

*      Seule la figure de la ligne(1) donne un triangle interne isocèle.

*      Les lignes (6) et (7) présentent deux figures où le triangle interne est isocèle avec la particularité de deux mesures contigües identiques (1 et 1 ou Phi et Phi.

 

 

Cas typiques

(cas des lignes (6) et (7) du tableau ci-dessus)

*      Les deux figures sont homothétiques: on passe de gauche à droite en multipliant toutes les mesures par Phi. L'aire est bien entendu multipliée par Phi².

*      Avec Pythagore et les relations sur les puissances de Phi, on calcule facilement la longueur des côtés du triangle interne. Exemple pour triangle en haut à gauche:

(1 + 1/ Φ)² + (1/ Φ)² = Φ ² + (2 – Φ) = (Φ + 1) + (2 – Φ) = 3

*      L'angle au sommet du triangle isocèle mesure 48,189° ().

 

 

Suite

*    Cercle, croissant et ellipse

*    Valeurs du nombre d'or

*    Construction

*    Trigonométrie

Aussi

*    Cercle

*    Constante Pi

*    Constantes Mathématiques

*    Construction géométrique des nombres

*    Série du type Fibonacci et cousins

DicoNombre

*    Nombre 1,618…