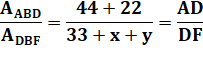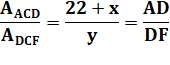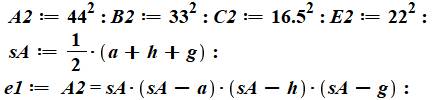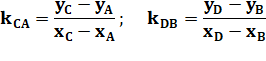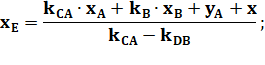|
Édition du: 08/10/2024 |
|
INDEX |
Problèmes – Défis |
||
![]()
|
Triangles dans triangle Un triangle
est partitionné en quatre
triangles. Retrouver l'aire de la réunion de deux d'entre eux. Le problème suivant est un défi à propos d'un
quadrilatère et ses diagonales. Pa simple ! |
||
|
|
Sommaire de cette page >>> Quatre triangles dans un triangle >>> Démonstration >>> Cinq triangles dans le triangle >>> Pour aller vers la résolution |
Débutants Glossaire |
|
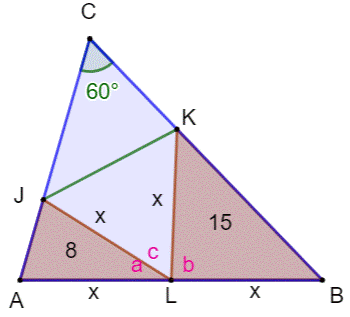
Construction Un triangle quelconque dont l'un des angles (C) vaut 60°. Sur le milieu L du côté opposé, on construit les
triangles isocèles
ALJ et BLK d'aires 8 et 15. On note x la longueur des côtés. Quelle est l'aire du quadrilatère
bleu CJLK ? Pistes 1)
Montrer que le triangle central JLK est équilatéral
et que son aire est donc connue en fonction de x. 2)
Développer, en conséquence, la connaissance des angles (figure du
bas). Notamment en J et K, la complémentarité des angles permet de dire que
les angles du triangle JKC sont égaux à a' et b'. 3)
Montrer, alors, que les triangles ABC et
KCJ sont semblables et que leur aires sont dans un rapport 4. 4)
L'aire des triangles AJL et LKB
sont connues. Calculer la valeur de x en
utilisant la formule
de l'aire avec les sinus pour les angles a et b, sachant que a + b =
120°. Alors, l'aire du triangle équilatéral JKL
sera connue 5)
L'aire du quadrilatère AJKB est désormais connue. Elle vaut trois fois
l'aire du triangle JCK. Laquelle ajoutée à l'aire du triangle équilatéral JKL
donne l'aire du quadrilatère demandé JLKC. Conseil: pour
suivre confortablement la suite de la démo, faire une capture d'écran de la
figure pour la garder sous les yeux. |
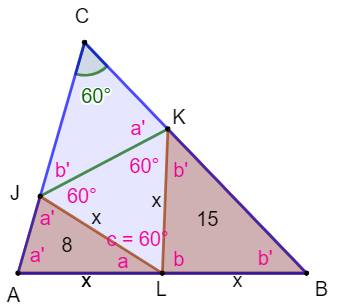
Les données du problème Calculer l'aire du quadrilatère bleu.
Valeurs des angles déduites du fait que JLK est équilatéral
|
|
|
Calcul des angles et du rapport des
aires du grand triangle au petit du haut
Calcul de l'angle a avec la formule
de calcul de l'aire en fonction du sinus
Voir Formule
du développement de sin (a – b) et autre formules trigonométriques Calcul de la longueur x et de
l'aire demandée
Voir Aire
du triangle équilatéral |
![]()
|
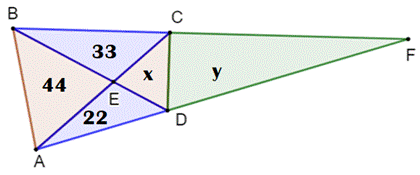
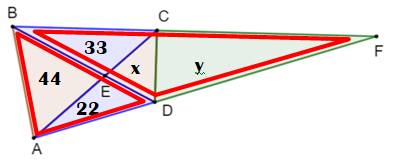
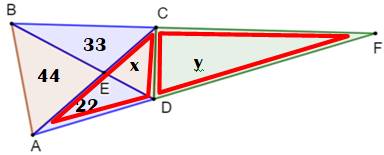
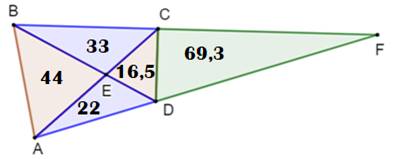
Construction Un triangle ABF. Deux points C et D sur les côtés AF et BF. Les segments AC et BD matérialisent quatre
triangles. L'aire de trois d'entre eux est connue. Trouver la valeur des aires x et y. Note: le
problème peut aussi s'énoncer sans le segment CD et demander l'aire de CEDF. |
Trouver les valeurs des aires x et y |
|
|
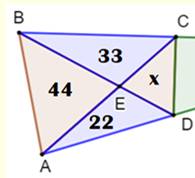
Deux théorèmes sont utilisés Le premier est relatif au quadrilatère
et aux quatre triangles découpés par les diagonales: le produit des aires
de deux triangles opposés est constant. 44 x = x = 22 × 33 / 44 = 33 /
2 = 16,5 |
Mise en évidence du quadrilatère
|
|
|
Le deuxième théorème est relatif à l'aire des triangles de même
sommet et de bases alignées. Le rapport entre les aires est égal au
rapport entre les longueurs des bases. En haut: En bas: |
Mise en évidence des triangles
|
|
|
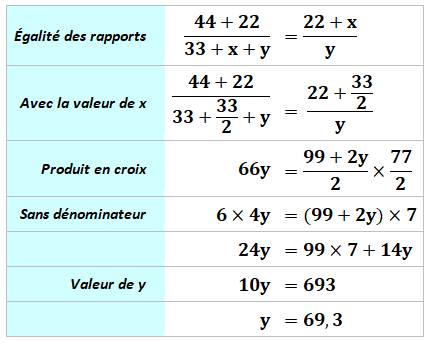
Calcul de x En rapprochant
ces deux égalités. Sachant que l'on
connait l'aire x = 33/2 Le tableau de
calcul montre que y = 69,3. |
|
|
|
Bilan x = 16,5 y = 69,3 Note: La
figure respecte les proportions. |
|
|
|
Solution algébrique Le quadrilatère ABCD est connu par l'aire des
quatre triangles formés par les diagonales. En théorie on peut le résoudre (trouver la
longueur des côtés) en utilisant la formule
de Héron liant les côtés à l'aire. Il s'avère que les solutions sont multiples et en
nombres infini. |
Exemple d'équations
Il est possible d'écrire huit
équations de cette sorte avec huit inconnues (4 côtés + 4 segments de
diagonales). Ces équations sont chacune
du quatrième degré. En pratique, insolvables. |
|
|
Solution par ajustement Avec un tableur,
introduire les coordonnées des quatre sommets du quadrilatère, calculer
l'aire des triangles avec la formule
analytique. Et, ajuster progressivement ces coordonnés pour atteindre
les aires connues. Inutile de dire que le processus est très long. |
Formule de l'aire du triangle selon
coordonnées des sommets
Formule des coordonnés du point d'intersection
des diagonales d'un quadrilatère
|
|
|
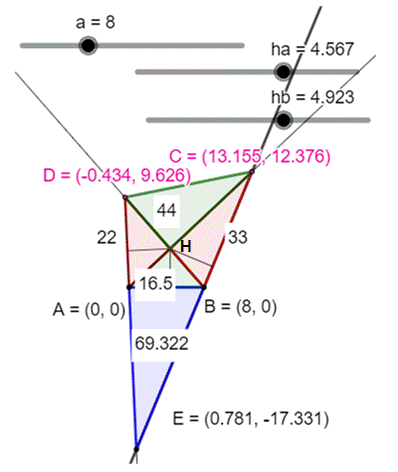
Solution avec GeoGebra Il est possible de construire une solution avec GeoGebra. La longueur AB est arbitraire, et elle est fixée
par le curseur a (ici AB = 8). Le pied de la hauteur est arbitraire sur AB. Notez qu'alors, nous avons deux degrés de
liberté. La longueur de la hauteur est fixée pour obtenir
une aire de 16,5 pour le triangle ABH. Les deux côtés du triangle ainsi défini sont
prolongés en attente des points C et D. Construction des deux triangles latéraux d'aires 22
et 33. Pour le
premier triangle, la hauteur est fixée par le curseur ha. Faire un cercle de
rayon ha centré sur le point central. AD est la tangente à ce cercle. Dessiner un segment AD dont la longueur est telle
que l'aire du triangle ADH soit égale à 22. Ajuster le curseur ha pour que le point D soit
sur le prolongement de BH. Même chose pour le triangle BHC d'aire 33.
Ajuster le curseur hb pour que C soit sur le prolongement de AH. GeoGebra permet de fortement zoomer de sorte que
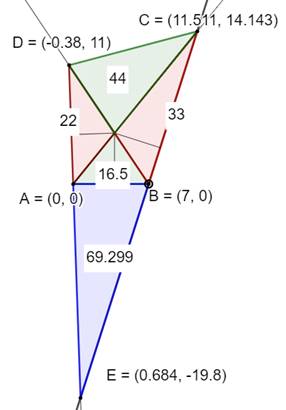
l'ajustement de ha et hb soit le plus précis possible. La figure du bas montre une solution avec AB = 7.
Les deux curseurs ont été à nouveau ajusté pour faire en sorte que les points
C et D soit sur AH et BH. |
Exemple avec AB =
8
Exemple avec AB =
7
|
![]()
|
Retour |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aExercic/Probleme/Trg4Trg.htm
|