NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/07/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométrie
Débutants Géométrie	TOPOLOGIE				Glossaire Topologie
INDEX Géométrie	Index	Introduction	Glossaire	Poincaré
	Quatre couleurs	Curiosités	Croisements	Nœuds
	Homéomorphisme	Variété	Chirurgie
	Sommaire de cette page >>> Approche >>> Équivalence >>> Invariants topologiques >>> Objets topologiques – Exemples

TOPOLOGIE – INTRODUCTION

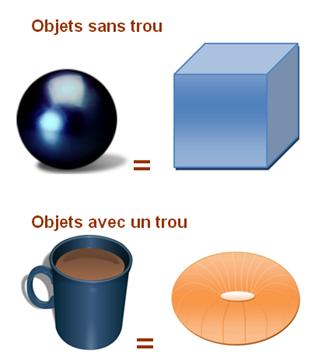
La topologie est un domaine spécifique de la géométrie où seules comptent les relations de voisinage et non les égalités, les distances, les mesures en général. Les topologues ignorent les angles et la forme exacte des objets.

En topologie, une sphère, un cube ou un verre, même à pied, sont tout à fait équivalents. Par contre, un verre et une tasse sont différents. La tasse avec son anse est équivalente à une chambre à air ou à un tore.

Sculptures de Carlo H. Séquin

APPROCHE

Une feuille de papier possède deux faces et un seul bord qui coure sur les quatre côtés de la feuille. Cette propriété subsiste même si la feuille est froissée ou pliée. Enroulez la feuille et vous la collez à ses extrémités: c'est un cylindre qui dispose toujours de 2 faces. Mais, désormais, ce tube possède deux bords: les deux cercles des extrémités. Les maths des nœuds font partie de la topologie. Comment les reconnaître, les classer à coup sûr? La topologie s'applique à bien distinguer la circonférence du cercle et sa surface, le disque. De même, elle distingue la surface de la sphère (la coquille) et son volume, la boule. Et itou pour les dimensions supérieures. Pour tout objet, sa surface de dimension n flotte dans un espace de dimension n+1. Un tel objet de dimension quelconque s'appelle une variété (ou manifold en anglais).

Équivalences topologiques
Deux objets sont équivalents du point de vue de la topologie, si on peut déformer l'un pour arriver à l'autre; comme s'il s'agissait d'objets en pâte à modeler. Aucune découpe n'est autorisée. La sphère est aplatie et elle se déforme en cube. La tasse à une anse (sans le café!) se déforme pour donner le tore; le trou de l'anse est conservé. Le bol, sans anse, est équivalent à la sphère. La tasse à deux anses est ce bretzel sont équivalents. Note: En topologie, ces objets sont des surfaces à deux dimensions qui flottent dans un espace à trois dimensions.	La topologie ignore les angles, mais fait cas de la quantité de trous.

Voir Sphère et Tore / Heptaèdre de Szilassi / Homéomorphisme

Caractéristiques ou invariants topologiques
Caractéristique	Description
	Exemple de la feuille de papier
Nombre de côtés	Nombre de faces: pour passer de l'une à l'autre, il faut franchir un bord.	2
Nombre de bords	Rupture entre l'objet et le monde extérieur.	1
Nombre chromatique	Nombre maximum de régions telles que chacune ait un bord commun avec toutes les autres. Voir les 4 couleurs	4
Nombre de Betti (1871)	Nombre maximum de coupures que l'on peut faire dans une surface sans la séparer en deux morceaux; la coupe est en travers d'un bord à un autre. Les nombres de Betti décrivent la connectivité des surfaces et des corps. Pour un objet à n dimensions, il y n+1 nombres de Betti: quantité d'éléments, de trous (ex: tore ou bretzel), et de cavités (ex: intérieur de la sphère-coquille). >>>	0
Coefficient de torsion	Témoigne de l'aspect plus ou moins tordu d'un objet, comme l'est le ruban de Moebius par exemple.
Caractéristique d'Euler-Poincaré	Caractérise les familles d'objets selon leur degré de décomposition en variétés premières, un peu comme les nombres entiers et leurs facteurs premiers.

Objets topologiques - Exemples
Objet	Côtés	Bords	Chromatique	Betti
Feuille	2	1	4	0
Tube	2	2	4	1
Sphère	2	0	4	0
Ruban de Moebius	1	1	6	1
Tore	2	0	7	2
Bouteille de Klein	1	0	6	2

Référence : Gardner : jeux mathématiques

Nombre de Betti et calcul quantique
Les nombres de Betti décrivent la connectivité des surfaces et des corps. Voir Définition			Deux structures ayant même nombre de Betti sont équivalentes
Enrico Betti est parmi les premiers à comprendre l'importance de la théorie de Galois. En 1871, il a introduit une suite d'invariants topologiques, que Poincaré a baptisés nombres de Betti. En 1915, James Waddell Alexander démontre que les nombres de Betti sont des invariants topologiques		Les nombres de Betti d'un objet en décrivent les caractéristiques, comme le nombre d'éléments qui le composent, ou le nombre de trous et de cavités qu'il possède. Un objet a un nombre de Betti de plus que le corps qu'il décrit a de dimensions. Les objets unidimensionnels, comme le cercle, ont deux nombres de Betti; les objets bidimensionnels comme les surfaces des boules, des couronnes de pain et des bretzels ont trois nombres de Betti. Le zéroième nombre de Betti compte de combien d'éléments se compose l'objet. Il vaut 1 pour le cube, la sphère, le cylindre. Le premier nombre de Betti précise le nombre de trous dans l'objet. Il vaut 1 pour le cercle ou pour la sphère (creuse), mais 0 pour la boule. Il vaut 2 pour la couronne, le trou visible et le trou interne (le tunnel circulaire). Pour plus de deux dimensions, le deuxième nombre de Betti indique combien de cavités sont cachées à l'intérieur de l'objet.
Plus précisément: (La définition mathématique dépasse le cadre de ces pages)		Informellement, le k-ième nombre de Betti correspond à la quantité de surfaces k-dimensionnelles indépendantes. Les premiers nombres de Betti sont définis intuitivement par : b0 est le nombre de composantes connexes; b1 est le nombre de courbes fermées indépendantes; b2 est le nombre de surfaces indépendantes.
Le calcul du nombre de Betti pour une structure donnée est très gourmand en puissance de calcul.			Les capacités des ordinateurs sont vite dépassées même pour des faibles valeusr de données.
Avec le calcul quantique, les choses semblent s'arranger.			En 2016, les chercheurs du MIT (Set Lloyd et al.) ont développé un algorithme quantique qui accélère grandement le calcul.
Et on commence à le montrer … modestement; mais ça marche !			En 2017, He-Liang Huang et al. (Université des Science et Technologie de Chine) ont implémenté l'algorithme sur un mini-calculateur quantique: processeur à six photons et analyse sur trois points à différentes échelles.
Quelques mots de vocabulaire anglais	Computationally demanding: exigent en puissance de calcul. That could dramatically speed up the calculation: qui pourrait accélèrer grandement le calcul.

Suite	Topologie – Glossaire Conjecture de Poincaré Conjecture du carré inscrit Les quatre couleurs
Voir	Bouteille de Klein Frises Géométrie – Index Pavage du carré Problème du mariage heureux Quatre couleurs Ruban de Moebius Théorème de Jordan
Bande dessinée	Le Topologicon – Lanturlu Une vulgarisation de la topologie en bande dessinée écrite par Jean-Pierre Petit
Sites	Topologie – Wikipédia Topologie – Initiation rapide – Claude Turrier – 95 pages Analysis situs – Topologie algébrique des variétés – CNRS – Cours en ligne
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Topologi.htm