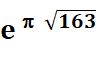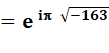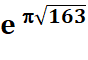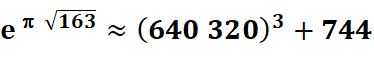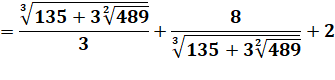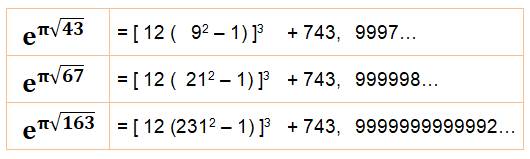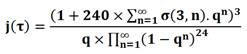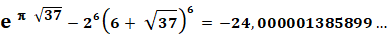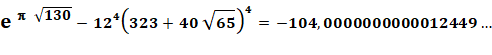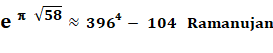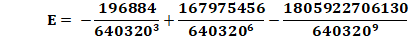|
||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRE 163 et les presque-entiers Constante dite de Ramanujan Certains nombres présentent la
particularité de s'approcher très près d'un nombre
entier; ce sont les nombres
presque entiers. Sur cette page nous développons ceux qui sont de
la famille de 163. Ce sont des nombres qui apparaissent en utilisant les
fonctions modulaires.
On trouve
ce nombre aussi sous la forme: e^pv163
(p pour pi et v pour racine) À leur sujet, plusieurs
questions se posent:
|
|
|
|
|
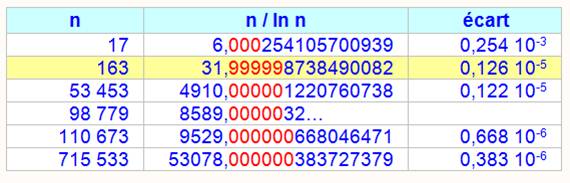
ln est le logarithme naturel ou népérien |
|
Voir Presque-entiers en sommes
|
|
||
|
Constante
de Ramanujan un nombre transcendant Anglais: Ramanujan's
constant Note: Il existe d'autres constantes
qui portent son nom. |
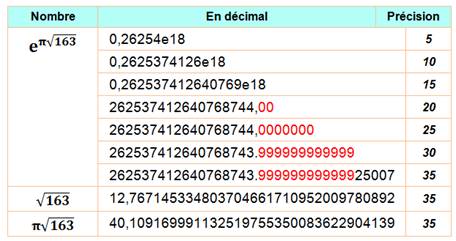
=
0,262… 1018 =
262 537 412 640 768 743, 999 999 999 999 2500
725971981856888793538563373... = Voir Exponentielle
puissance Pi = e 40,109 169
991… = 2,718281828… 40,109
169 991… =
640 3203 + 743 + 0,999 999 999 999
2500… =
123 (2312 – 1 )3
+ 743 + …. =
218 . 33 . 53 . 233 . 293
+ 743 + …. |
|
|
N - |
=
0,7499274… 10-12 Distance à l'entier le plus
proche. |
|
|
Approximation
sympathique |
Soit: 262537412640768744 Pour:
262537412640768743,999… Écart:
7, 5 10-13 |
|
|
Approximation
avec 19 chiffres significatifs: partie entière et une décimale. |
Pour information: Racine de l'équation: 5,31862821775018565910…
|
|
|
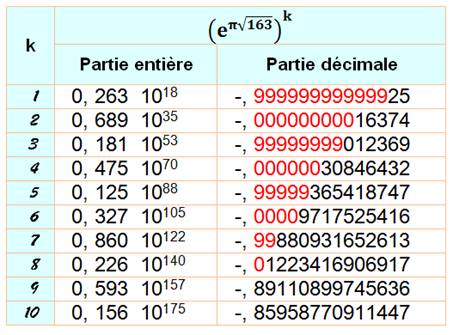
Puissances
(k) et décroissance de la persistance des presque-entiers |
|
|
|
Presque
entier, surprenant! |
Car e comme Pi sont
des nombres transcendants. Leurs chiffres
ne se répètent jamais, ne présentent pas de motifs particuliers; il sont
aléatoires. Pourtant, le fait que ce nombre soit proche d'un entier n'est pas
fortuit. Il est lui-même transcendant. |
|
|
Piste? |
163 = – (1 – 4 x 41) Et on trouve 41 dans la célébres suite de nombres premiers
donnée par Euler: x² – x + 41 >>> Effectivement les nombres de Heegner
intervinnent dans la caractérisation des nombres premiers. |
|
|
Sur le modèle de Ramanujan |
|
|
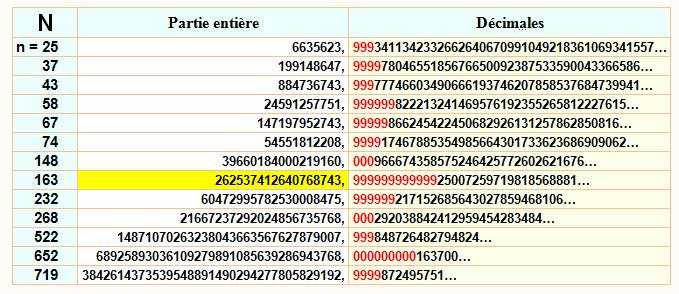
Exploration
de
N =
Présentation avec
50 chiffres
Relations
particulières avec des cubes
Voir Nombre
744 Il est remarquable de trouver ces valeurs
entières à mieux que 1/1000è près.
et, il est bien connu qu'en théorie des
fonctions modulaires, la fonction j de tau est invariante dans le groupe des
transformations unimodulaire … et …
est un nombre entier. Or -1/q est la
constante de Ramanujan. Comme q est petit, 1/q est proche d'un entier. Cette
formule permet également d'expliquer pourquoi les puissances sont de moins en
moins proches d'un entier. Le groupe
monstre n'est pas loin de toutes ces théories … Ramanujan
et 1/Pi Ramanujan
à moins de 20 ans élabore une formule
très efficace pour calculer Pi. Elle est basée sur la coïncidence numérique:
Voir Nombre
104 |
|
Avec le nombre d'or et le nombre d'argent
|
Nombre
d'or
|
Nombre
d'argent
|
Voir Nombre d'or
/ Nombre
d'argent
![]()
Bilan des
recherches faites par Antony Canu
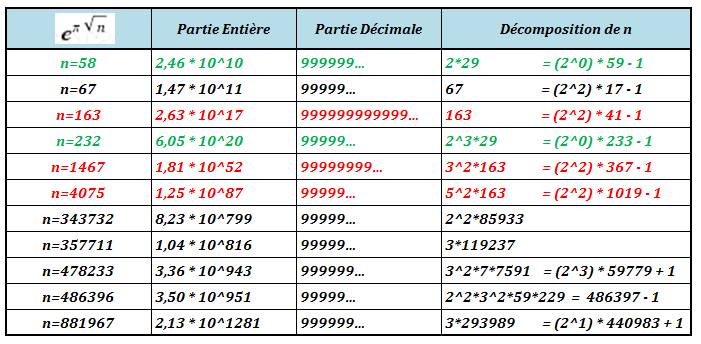
Ses plus grands
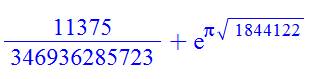
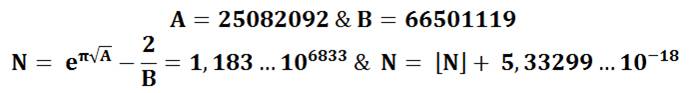
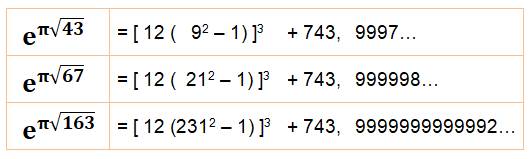
Voir La
constante de Ramanujan est elle la plus proche d'un entier ? – Anthony Canu
![]()
|
|
|||
|
–1, –2, –3, –7, –11, –19, –43, –67, et –163 |
|
||
|
Nombres
de Heegner – Théorie avancée des nombres
Définition Nombre de Heegner: entier sans facteur carré n
positif tel que l'anneau des entiers du corps quadratique imaginaire Équation Rabinowitz a
montré, en 1913, que x² + x + p
représente le nombre maximal de
nombres premiers consécutifs si et seulement si x² + xy + py² est la
seule classe d'équivalence de forme quadratique binaire positive de par son
discriminant. Cette condition est appelée classe
numéro un. Pour les discriminants négatifs, l'ensemble de ces
discriminants est fini; ce sont les nombres de Heegner. Voir sites Heegner number de Mathworld / Heegner Number de Wikipedia |
|||
|
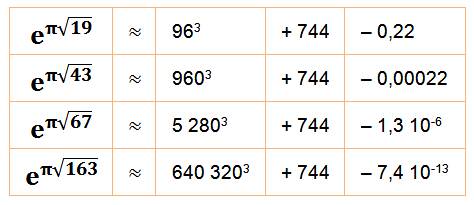
Approximation pour les quatre plus grands nombres de Heegner |
|
||
|
Autres écritures |
|
||
|
Autres curiosités |
|
||
|
Approximation de Pi avec 30 à 75 chiffres |
En prenant E = 0, Pi est donné avec
30 décimales. En tenant compte de l'écart E (connu),
il est possible de poursuivre les calculs et d'obtenir une approximation de
Pi avec 75 décimales:
|
||
|
Vittorio
ORNAGO me signale cette curiosité à propos des nombres de Heegner: Hors les nombres 1 et 7, ces nombres deviennent des carrés en leur ajoutant 6 ou 14. |
|
|
|
|||
|
Il est probable
que la détection des nombres en exposant, tel que 163, résulte de réflexions
sur les fonctions modulaires, elles-mêmes suscitées par la résolution de
certaines équations du cinquième
degré (voir Hermite). |
Cependant, les premiers mathématiciens à les avoir découverts donne
leur valeur précise. En 1859, Hermite cite la valeur du nombre en racine de
43 et précise que celui en racine de 169 possède douze 9. Quels sont leurs méthodes de calcul? |
||
|
Aujourd'hui |
Les
logiciels de calcul donnent la précision que vous voulez. Les calculs
présentés sur cette page ont été réalisés avec Maple. La calculatrice de votre
ordinateur devrait également faire l'affaire. |
||
|
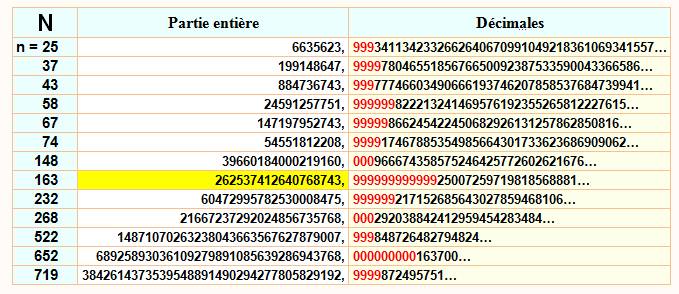
Hier, sans les calculateurs? |
Le calcul
devait être très long avec risques d'erreurs et, surtout, comment choisir la
quantité de décimales
pour être sûr d'atteindre le résultat souhaité? Ce
tableau montre que:
|
||
|
Calcul de la racine |
Il
existe des méthodes pour calculer les racines: la méthode de Héron ou la méthode que l'on apprenait autrefois
et qui ressemble à une division posée. Voir
le site Racine
carrée à la main de Thérèse Eveilleau |
||
|
Valeur de Pi |
Dans
les années 1800, la valeur de Pi
est connue avec 200 décimales et plus. Surprise
le produit est proche de 40. Alors, existe—t-il une astuce pour en calculer
facilement l'exponentielle? |
||
|
Exponentielle |
Feynman est connu
pour son astuce de calcul des exponentielles (de tête!), mais pas possible
pour de telle taille. Passage
par les logarithmes et les tables de logarithmes. La quantité de décimales ne dépassait pas 27 (à ma
connaissance). |
||
|
Bilan |
Avant
les ordinateurs, le calcul direct
de |
||
|
|
|
|
En fait: écart = 0,75 10-12
|
|
|
|
Cité par
François Le Lionnais – Les
nombres remarquables |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()