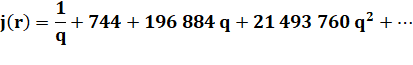|
|||||||||||||||||||||||||||||
![]()
|
Le MONSTRE est une prédiction théorique de la théorie des
groupes, un domaine de géométrie qui traite des propriétés symétriques des
objets. Dans les années 1970, les mathématiciens ont commencé à
créer une sorte de tableau périodique de groupes : ils voulaient trouver les "atomes"
associés aux groupes. De sorte que chaque groupe fini serait représenté par
une combinaison de ces "atomes". Après des décennies de recherche, on trouve qu'il existe
un nombre infini de "groupes simples finis", mais presque tous
peuvent être divisés en 18 catégories. Cependant, il en reste 26 qui ne
rentrent pas dans ces 18 classes. Le premier de ces cas aberrants était le MONSTRE, que les
mathématiciens Bernd Fischer et Robert Griess avaient prédit en 1973. Ce nom est
dû à sa taille: il contient plus de 8 x 1053 symétries. A titre de
comparaison, le groupe de symétrie D20 à vingt faces (un icosaèdre) contient
60 symétries, ce qui signifie que soixante transformations (rotations ou
réflexions) peuvent être réalisées sans changer l'orientation du D20. La plupart des mathématiciens pensait qu’il allait être impossible
de construire le monstre avec l'informatique de cette époque. Pourtant, en 1980, Griess a construit le monstre et a
ainsi prouvé son existence – sans l'aide d'ordinateurs. |
|
|
|
|
Note: nombres premiers absents: 31, 43,
53, 61 et 67. |
|
|
Terme anglais conçu par John Horton Conway et
Simon P. Norton en 1979, utilisé pour décrire la connexion, alors totalement
inattendue, entre le groupe Monstre M et les formes modulaires (en
particulier la fonction j ).
Il s'avère que derrière Monstrous Moonshine se
trouve une certaine théorie des
cordes ayant le groupe Monstre comme groupe de symétries. |
Voir Monstrous moonshine
– Wikipedia
|
|
|
|
x-1 + 744 +
196 884 x + 21 493 760 x2 +864 229 970 x3 + …
1 + 193 883 = 193 884 1 + 193 883 + 21 296 876 = 21
493 760 Etc. avec des relations plus compliquées! Illustration de formes modulaires en couleurs
Source: The
modular group PSL 2(Z) – Wikimedia Commons |
|
|
|
|
|
|
|
|
John
Conway suppose que le groupe monstre ne peut pas exister sans une bonne
raison. Mais je n'ai aucune idée de quelle est telle, explique-t-il. Avant
de mourir, je voudrais comprendre pourquoi il existe. Mais je suis presque
certain que je ne le saurai pas. C'est
le genre de beauté qui existe dans le monde abstrait, mais nous pauvres
mortels ne pourrons jamais la voir. On peut juste voir de vagues lueurs. |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Outils/Outils/Structur/Monstre.htm
|
![]()