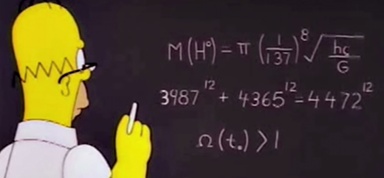NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/03/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Puissances
Débutants Logarithmes	Opérations sur les puissances		Glossaire Puissances
Rubrique PARTITION INDEX PUISSANCES	Somme de puissances	Carré somme de cubes
	Th de Pythagore	Th de Fermat-Wiles
	Démonstration du théorème	Fermat pour n = 4 (démonstration)
		Fermat pour n = 3 (démonstration)
		Sommaire de cette page >>> Approche >>> Théorème de Fermat – Wiles >>> Fermat et les Simpsons >>> Historique >>> Wieferich >>> Démonstration - Principe >>> Généralisation >>> Amusement

Grand théorème de Fermat

ou

Dernier Théorème de Fermat

devenu

THÉORÈME DE FERMAT-WILES

aussi

Théorème de Fermat – Wiles – Taylor

Zⁿ = Xⁿ + Yⁿ

PUISSANCE = SOMME DE 2 PUISSANCES

IMPOSSIBLE, sauf pour les carrés

Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere: Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caperet. (Or il est juste de diviser un cube en deux cubes, ou un carré-carré en deux carrés-carrés, et en général pas de pouvoir à l'infini au-delà du carré en deux du même nom. Bien sûr, j’ai découvert une merveilleuse démonstration mais la marge trop petite ne la contiendrait pas.)

Fermat dit qu'il en a la preuve. Ce qui est extrêmement peu probable.

La démonstration pour de nombreuses valeurs particulières de n existe.

Mais, nombreux sont ceux qui se sont attaqués à la démonstration générale, en vain.

Wiles a réussi (1993), mais avec l'arsenal des outils mathématiques les plus avancés d'aujourd'hui.

Sa démonstration fait des incursions dans diverses rubriques très pointues des mathématiques modernes,.

Anglais: Fermat's Last Theorem (FLT)

APPROCHE

Pythagore: puissance 2 Le triplet de Pythagore le plus célèbre: 3² + 4² = 5² Il existe une infinité de triplets de Pythagore. Fermat : puissance 3 et au-delà Tentons notre chance! 6^3 + 8^3 = 9^3 – 1 216 + 512 = 729 – 1 Oui, mais raté … à un près! Il n'existe pas de cas Fermat pour la puissance 3, comme pour toutes les autres plus grandes. Autre cas célèbre: 9^3 + 10^3 = 1729 et 1728 = 12^3. Voir Nombres Taxicab

THÉORÈME DE FERMAT – WILES

Puissances 3, 4 … X^3 + Y^3 = Z^3 X^4 + Y^4 = Z^4 Etc. Aucune solution (Voir démonstration) La relation exprimée simplement: X^n + Y^n = Z^n N'A AUCUNE solution en nombres entiers pour n > 2. Formulation précise Si n est un entier supérieur à 2, l'équation X^n + Y^n = Z^n n'a pas de solution, avec X, Y, Z entiers non nuls Formulation mathématique Pour tout n > 2 n'a pas de solution pour Exemples Pour n = 2 : il s'agit des triplets de Pythagore. Exemple : 3² + 4² = 5² Pour n = 3 : on peut donner 1^3 + 1^3 = ( ^32 )^3 , mais ^32 = 1,259… n'est pas un entier

Fermat et les SIMPSONS: 1 782^12 + 1 841^12 = 1 922^12

Curiosité Une égalité qui contredit le théorème de Fermat proposée par les Simpsons. Où est la supercherie? Calcul – C'est pourtant vrai … Prendre votre calculette avec dix chiffres significatifs et faites: A + B = 1 782^12 + 1 841^12 et S = 1 922^12 A = 1,025397835 e+39 (e+39 veut dire 10^39) B = 1,5158124229 e+39 A + B = 2,541210259 e+39 S = 2,541210259 e+39 Ainsi: 1 782^12 + 1 841^12 = 1 922^12 Explications – Finalement non! Avec la calculette de votre ordinateur (ou même sur Google: tapez simplement 1782^12 dans la fenêtre de recherche et vous aurez le résultat immédiat). A = 1,0253978356226336348075504629482e+39 B = 1,5158124229919555414811194951942e+39 A + B = 2,5412102586145891762886699581424e+39 S = 2,5412102593148014108192786496437e+39 S – (A+B) = 0, 700 212 234 530 608 691 501 223 040 959e+30 La somme est presque juste. La différence est pourtant un nombre comportant 30 chiffres. L'égalité est en fait: 1 782^12 + 1 841^12 = 1921,99999995586…^12 Pour information A + B compte six facteurs: A + B = 409 x 4793 x 7793 x 577513 x 17960641 x 16036943149450969 Un autre exemple des Simpsons tout aussi faux 3 987^12 + 4 365^12 = 4 472^12 cette somme vaut en fait: 4472,000000007059290…^12 Supercherie révélée immédiatement avec la théorie des nombres Explication 1: la parité d'un nombre élevé à une puissance est conservée. Dans le premier cas: 1 782^12 + 1 841^12 = 1 922^12 on a P + I = P ce qui est impossible. Dans le second cas: 3 987^12 + 4 365^12 = 4 472^12 on a I + I = P ce qui est possible. Explication 2: divisibilité par 3 (qui est conservée lorsqu'on élève à une puissance). Pour le deuxième exemple, les deux premiers termes sont divisibles par 3 alors que celui de la somme ne l'est pas. L'égalité ne peut pas tenir.

Voir Les nombres en 8000 par les Simpsons / Bender et Flexo les robots de Futurama

HISTORIQUE – Chronologie
1637	Pierre de Fermat	Il annote l'Arithmetica de Diophante , traduction de Bachet. pas de cubes, pas plus que de puissances quelconques qui satisfassent l'équation. j'ai une démonstration merveilleuse, mais la marge est trop étroite pour la contenir.
1670	Clément Samuel fils de Fermat	Publication de l'Arithmetica de Diophante avec les observations de Fermat.
1753	Euler	Preuve pour n = 3, avec une erreur récupérable en lisant d'autres démonstrations d'Euler.
vers 1800	Sophie Germain Legendre	Pas de solution jusqu’à x, y et z divisibles par n jusqu'à 100. Extension jusqu'à 197.
1825 1832	Dirichlet	Prouve le cas n = 5. Prouve le cas n = 14.
1839 1847	Gabriel Lamé	Prouve le cas n = 7. Prétend avoir trouvé la solution complète.

Prix Wolfskehl

Paul Wolfskehl, mathématicien né en 1856 à Darmstadt, promet une récompense à quiconque pourrait retrouver la preuve de Fermat (environ un million d'euros, mais devenu 30 000 euros pour Wiles du fait de l'inflation en Allemagne après la première guerre mondiale). Pourquoi cette générosité? La raison est controversée.

Est-ce l’attachement de Wolfskehl à une mystérieuse jeune femme, jamais identifiée. La femme le repoussa. De désespoir, il décida de se suicider d'une balle dans la tête à minuit pile. En attendant, il se rendit dans sa bibliothèque et commença à feuilleter des documents de mathématiques.

Il tombe sur le travail d'Ernst Kummer (1810-1893), qui avait démontré qu'il y avait une erreur dans la preuve du dernier théorème d'Augustin Cauchy (1789-1857). Piqué au vif, il tente de prouver que Kummer avait tort et que la preuve de Cauchy nécessitait simplement une légère mise au point. Il travaille jusqu'à l'aube pour constater que Kummer avait bel et bien raison. La conjecture de Fermat résiste.

Le délai de minuit est passé! Wolfskehl est tellement enthousiasmé par les mathématiques qu'il abandonne l'idée du suicide et décide de créer le fameux prix.

Une autre source explique que Wolfskehl, forcé de rester en chaise roulante, ne pourra pas être docteur. Alors, il s'est tourné vers les mathématiques. Le prix aurait été créé en hommage à cette nouvelle vie.

Une autre source dit qu'on l'aurait obligé à épouser une garce et que le prix ainsi mis en jeu échappait à sa succession.

D'après Fermat’s Last Theorem and the Wolfskehl Prize – Simon Singh – 1997

1908	l'Université de Göttingen en Allemagne	Offre un prix de 100 000 marks à qui trouvera la démonstration avant 2007.
1968	Shimura- Taniyama -Weil	Conjecture STW: toute courbe elliptique provient d'une forme modulaire.
1970	Serres	Conjecture qui concerne les formes modulaires.
1983	Gerd Faltings	Nombre fini de premiers entre eux qui seraient solution de l'équation.
1985	Frey & Ribet	Conjecture de Frey démontrée par Ribet en 1986: si des courbes vérifient la conjecture STW, elles vérifient aussi la conjecture de Serre.
23 juin 1993	Andrew Wiles	Conférence annonçant la démonstration du théorème de Fermat.
Nov.1993		Rumeur concernant une défaillance dans la démonstration.
3 avril 1994	Noam Elkies	Il annonce avoir trouvé un contre-exemple à la conjecture de Fermat ou presque >>>
25 Oct.1994	Andrew Wiles Richard Taylor	Mise à jour de la démonstration du Dernier théorème de Fermat : preuve finale.
Mai 1995	Andrew Wiles	Publication dans les Annals of Mathematics.
27 juin 1997	Andrew Wiles	Attribution du prix Wolfskehl de 50 000 $.
1999	Christophe Breuil, Brian Conrad, Fred Diamond et Richard Taylor	Conjecture de Taniyama–Shimura complètement démontrée. La partie suffisante pour en déduire le dernier théorème de Fermat a été démontrée par Andrew Wiles. Ces mathématiciens ont traité les cas restants en s'inspirant des travaux de Wiles.

Presque Fermat

Noam Elkies a trouvé des cas où l'égalité de Fermat-Wiles est presque réalisée. Exemples:

280¹⁰ + 305¹⁰ = 316¹⁰ (1 + 2,31 10^-9)

3 472 073⁷ + 4 627 011⁷ = 4 710 868⁷ (1 + 3,63 10^-22)

Même ce cas avec de plus petits nombres:

13⁵ + 16⁵ = 17⁵ + 12 = 15⁵ (1 + 8,45 10^-5)

avec 13 + 16 = 17 + 12

HISTORIQUE (suite)

Historique: Les démonstrations pour prouver cette relation jusqu'à n < 269 existaient en 1961. Fermat, dans la marge du livre " Arithmétique " de Diophante, avait noté en 1637 qu'il avait découvert la démonstration mais n'avait pas la place de la noter. Fermat avait sans doute vu des cas particuliers non évidents, ou autres, mais il est peu probable qu'il ait eu la solution complète. La preuve a résisté à 350 ans d'efforts. Découverte: En 1993, Andrew Wiles publiait la démonstration générale en 151 pages. Il reconnu immédiatement qu'il y avait une erreur. Il a fallu 10 mois à A. Wiles et R. Taylor pour présenter une version améliorée, que les experts estiment correcte. Seuls 200 mathématiciens au maximum au monde sont capables de saisir tous les détails de la démonstration. La démonstration fait un long détour par la théorie des nombres et la géométrie algébrique pour se terminer par la preuve du théorème de Fermat. Au passage, la démonstration laisse des démonstrations générales plus fortes et plus importantes dans ses applications. C'est probablement la démonstration la plus épluchée de l'histoire des mathématiques. Contributeurs Quatre mathématiciens sont à l'origine de la réussite de Wiles Gerhard Frey, Jean-Pierre Serre, Ken Ribet, Richard Taylor. Andrew Wiles: prix Abel 2016 >>>

En 1909, Wieferich démontre que :
Si x^p + y^p = z^p admet une solution avec p premier impair qui ne divise pas x, y ni z …	… Alors 2^p – 1 – 1 est divisible par p² Ce qui limite les recherches

Voir Nombre 1093 / Paires de Wieferich

DÉMONSTRATION – Principe

Cette preuve est fondée sur les propriétés des courbes elliptiques pour lesquelles Gerhard Frey, une dizaine d'années auparavant, avait montré la connexion avec le théorème de Fermat. Il avait montré que les solutions de l'équation pour n > 2 engendraient une étrange classe de courbes elliptiques semi - stables, qui infirmaient une autre conjecture fameuse, la conjecture de Shimura – Taniyama – Weil (STW). En 1986, Kenneth Ribe de l'université de Californie, prouva que si cette conjecture était vraie, au moins pour les courbes elliptiques semi - stables, alors le théorème de Fermat en découlait. Lors de la première tentative, A. Wiles avait eu une approche " directe ", mais commettait une généralisation abusive. Ce qu'il a corrigé en trouvant une voie détournée. La démonstration suppose la consistance du système formel Zermelo-Fraenkel. Pour information: une démonstration ultrasimple découlerait de la résolution de la conjecture ABC (annoncée en 2013).

Voir Petit théorème de Fermat

Shimura – Taniyama – Weil (STW)

1994 – Démonstration du théorème de Fermat par A. Wiles y compris la conjecture STW sous une forme partielle (courbes elliptiques semi-stables). 2000 – Démonstration de la conjecture STW dans sa forme complète, suite à un travail d'équipe: Richard Taylor, Fred Diamond, Brian Conrad … y compris les français: Laurent Lafforgue, Loïc Mérel et Christophe Breuil, un jeune polytechnicien français qui a finalisé la démonstration.

GÉNÉRALISATION

Fermat suite… De nombreuses applications des équations à la Fermat ont été développées. En particulier, la conjecture de Dénes (1952) qui est devenue le théorème de Darmon et Merel (1995). X^n + Y^n – 2 . Z^n = 0 Possible que pour X = Y quand n ³ 3 et solutions triviales: (1, -1, 0) (1, 1, -1) Note Cette relation est importante dans l'analyse des carrés magiques de nombres carrés 3x3 où la somme des sommets opposés vaut deux fois le nombre central: x² + y² = 2 z². >>> Généralisation X^n + Y^n + A^m . Z^n = 0 Résolu pour A = 2 et m = 1: ci-dessus. Résolu pour n > 10, m > 0 et certaines valeurs de A comme 3, 5, 7, 11, 13, 17, 19, 23, 29, 53, 59 par Darmon et Merel. Autres équations X^n + Y^n = Z^2 X^n + Y^n = Z^3 A.X^n + B.Y^m = C.Z^p Objet de recherches actuellement X^n + 2Y^n = 4Z^n Impossible pour n > 2 (X, Y, Z entiers positifs) Assez facile à prouver (car pas de solution 2-adiques non triviales) Cas du bicarré 422 481^4 = 95 800^4 + 217 519^4 + 414 560^4 Il existe une infinité de puissances 4, somme de 3 puissances 4

Retour à Somme de puissances / Voir Équations diophantiennes

AMUSEMENT – Contre-exemple

sans retenue!

Contre-exemple !

70^3 =		3	4	3	0	0	0
+ 212^3 =	9	5	2	8	1	2	8
462^3 =	9	8	6	11	1	2	8

C'est le 11 qui ne manque pas de retenue …

Trouvé par Erich Friedman / Cité par Ed Pegg Jr

Suite	Démonstration via la conjecture ABC Étude du cas des cubes Fermat Fermat pour E42 La conjecture de Fermat – Roman Presque Fermat (à un près) Somme de trois cubes – Cas de 33, 42, 74 et autres Théorème de Fermat et Waring Théorème de Mordell-Faltings Triplets de Pythagore
Voir	Bi, tripartitions Cercle Conjecture - Glossaire Conjecture ABC Conjecture de corrélation gaussienne Conjecture de Poincaré (Théorème de Poincaré-Perelman) Conjecture de Riemann Conjecture d'Euler Démonstration Nombre = sommes de puissances Nombre divisible par premiers Nombres carrés Nombres de Gauss généralisés comme tentative de solution Nombres polygones Nombres triangles Partition en somme de puissances Partitions Petit théorème de Fermat Pythagore  Somme multi puissantes Théorie des nombres Triangle – Index Unité des puissances
Livres	La conjecture de Fermat – Jean d'Aillon – JC Lattès – 2006. Le dernier théorème de Fermat - Simon Singh - Relate l'aventure de A Wiles - un film a été réalisé sur ce thème et par la même personne: S Singh VOIR LE FILM EN FRANÇAIS >>> Invitation aux mathématiques de Fermat - Wiles - Yves Hellegouarch - pour connaisseurs avec bonnes bases mathématiques Qu'est-ce que l'Univers - L'énigme du théorème de Fermat - Yves Hellegouarch - texte de conférence donnée en juin 2000
Site	Une aventure mathématique, le théorème de Fermat - Jeanne VIGOUROUX et al. – pdf46 pages
Sites (Niveau élevé)	Fermat's last theorem – MacTutor Historyof Mathematics archive Fermat, Wiles et GL(2) – Guy Henniart The Solving of Fermat’s Last Theorem – Karl Rubin – Diaporama 46 vues The proof of Fermat's last theorem – Nigel Boston – 2003 – pdf 140 pages
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/ThFermat.htm