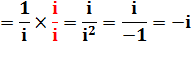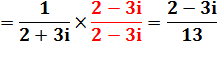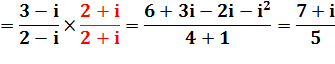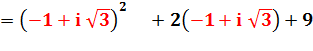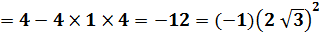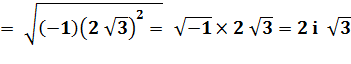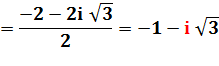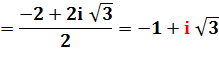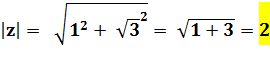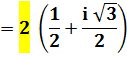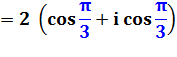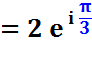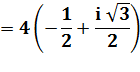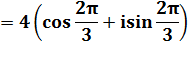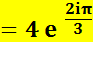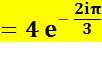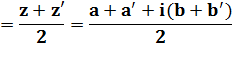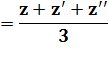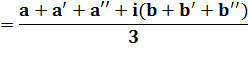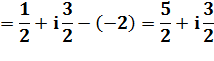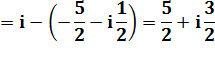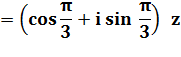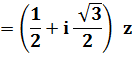|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres complexes Technique opératoire Nous allons passer en revue
diverses techniques de calcul avec les nombres complexes qui se retrouvent dans
les problèmes typiques posés en terminale, notamment au bac. |
Données communes
|
Deux
nombres complexes: z = a
+ ib,
affixe d'un point M (ou du vecteur z'
= a' + ib', affixe d'un point M' (ou du vecteur Ne
pas prendre cette notation
pour une dérivée; nous aurions pu
choisir zA et zB. Se
souvenir que ib veut dire i multiplié par b. En cas
de confusion possible écrire i.b |
|
|
|||
|
Ne pas confondre Affixe et Module |
|
Affixe du point M ou du vecteur
C'est le nombre complexe lui-même. Module de z, ou longueur OM. |
|
|
Calcul avec i² = – 1 |
|
|
|
|
Conjugué
|
|
|
|
|
Dénominateur complexe |
|
|
|
|
|
|
||
|
|
|||
Suite Opérations avec
les complexes et leur interprétation vectorielle
Voir Exercices
Voir Équation du second degré / Racines avec les négatifs
|
|
|||
|
Calcul du module |
|
|
|
|
Détermination de l'angle (argument) |
|
Voir Explications |
|
|
Forme exponentielle |
|
|
|
|
|
|||
Suite en Forme polaire
|
Avant
toute chose extraire le module
est le mettre en facteur. En
suite, les deux termes du nombre complexe caractérisent un angle:
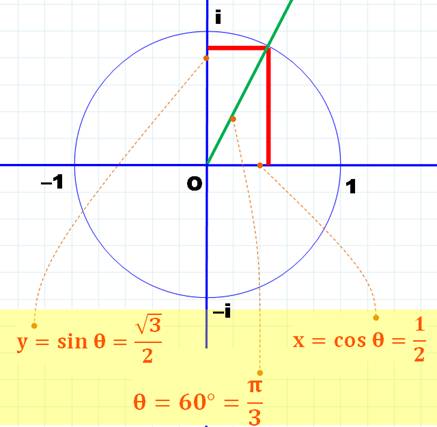
Un
petit retour sur le cercle trigonométrique qui montre comment lire la valeur
de l'angle. Astuce: commencez par repérer le ½ et vous aurez pratiquement la
réponse pour 30° et 60°.
En classe de terminale, sauf cas
extraordinaire, les angles à trouver seront en 30°, 45° et 60° (et leur
associés autour du cercle). Souvenez-vous que Pi = 180° et calculez
facilement les valeurs en radians. Par
exemple 60° est le tiers de 180°, soit Pi/3 en radians. |
Voir Trigonométrie
|
|
|||
|
Nombre complexe |
|
|
|
|
Son conjugué |
|
|
|
|
Module |
|
|
|
|
Détermination de l'angle pour z1 Passage par la forme trigonométrique |
|
|
|
|
Pour z2 |
|
|
|
|
|
|||
Suite en Forme
exponentielle
Voir Autres identités
trigonométriques
|
|
|||
|
Point milieu H de MM' |
|
|
|
|
|
|
||
|
Vecteurs égaux (équipotents) MM' et PP' Formation d'un parallélogramme
Si
(m' – m) = (p' – p) m,
m', p et p' sont les affixes des points |
|
Le quadrilatère MM'PP'
est un parallélogramme. |
|
|
|
|||
Voir Centre de gravité /
Géométrie
|
DROITE |
Voir Recherche du rayon et du
centre du cercle ![]() (Notion
très importante pour la terminale)
(Notion
très importante pour la terminale)
Voir Rotation
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()