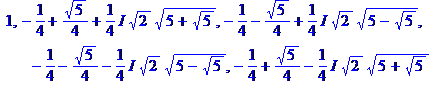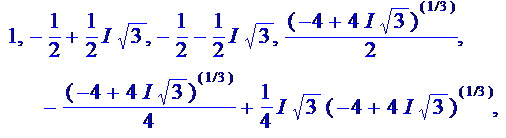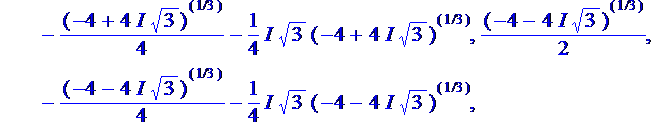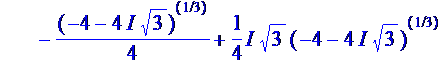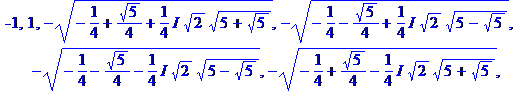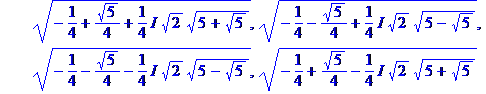|
|||||||||||||||||||||||||||||
![]()
|
RACINES DE L'UNITÉ & Polynômes cyclotomiques Résolution générale de
l'équation: zn = 1 <<< Voir
Introduction |
|
|
||
|
|
zn = 1
Car: 1 = cos(0) + i sin (0) 1 =
1 + 0 Rappel: 2 |
|
|
Rappel: racine
carrée est équivalent à puissance
1/2 |
x = { cos(2 |
|
|
|
x = cos(2 |
|
|
Lire: oméga égal … |
|
|
|
En utilisant la formule de De
Moivre. |
|
|
|
|
||
|
|
|
|
|
Exemple pour n = 3 1 + ( –
0,5 + 0,5 { 2 – ( – 0,5 + 0,5 Exemple pour n = 4 1 + (– 1)
+ i + (– i) = 0 { 2 – (–1) } { 2 – ( i )
} { 2 – ( –i ) } = 5 |
||
|
|
ou
polynômes cyclotomiques |
|
|
|
N |
Les
racines de ces équations sont les racines nièmes
complexes de l'unité |
|
|
1 |
x
– 1 |
|
|
2 |
x + 1 |
|
|
3 |
x2 + x
+ 1 |
|
|
4 |
x2 + 1 |
|
|
5 |
x4 + x3
+ x2 + x + 1 |
|
|
6 |
x2 – x
+ 1 |
|
|
7 |
x6 + x5
+ x4 + x3 + x2 + x + 1 |
|
|
8 |
x4 + 1 |
|
|
9 |
x6 + x3
+ 1 |
|
|
10 |
x^4 – x^3 + x^2 –
x + 1 Notation ^ pour puissance |
|
|
11 |
x^10 + x^9 + x^8
+ x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x + 1 |
|
|
12 |
x^4 – x^2 + 1 |
|
|
13 |
x^12 + x^11 + x^10
+ x^9 + x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x + 1 |
|
|
14 |
x^6 – x^5 + x^4 –
x^3 + x^2 – x + 1 |
|
|
15 |
x^8 – x^7 + x^5 –
x^4 + x^3 – x + 1 |
|
|
16 |
x^8 + 1 |
|
|
17 |
x^16 + x^15 + x^14
+ x^13 + x^12 + x^11 + x^10 + x^9 + x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + x^2 +
x + 1 |
|
|
18 |
x^6 – x^3 + 1 |
|
|
19 |
x^18 + x^17 +
x^16 + x^15 + x^14 + x^13 + x^12 + x^11 + x^10 + x^9 + x^8 + x^7 + x^6 + x^5
+ x^4 + x^3 + x^2 + x + 1 |
|
|
20 |
x^8 – x^6 + x^4 –
x^2 + 1 |
|
|
21 |
x^12 – x^11 + x^9
– x^8 + x^6 – x^4 + x^3 – x + 1 |
|
|
22 |
x^10 – x^9 + x^8
– x^7 + x^6 – x^5 + x^4 – x^3 + x^2 – x + 1 |
|
|
23 |
x^22 + x^21 +
x^20 + x^19 + x^18 + x^17 + x^16 + x^15 + x^14 + x^13 + x^12 + x^11 + x^10 +
x^9 + x^8 + x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x + 1 |
|
|
24 |
x^8 – x^4 + 1 |
|
|
25 |
x^20 + x^15 +
x^10 + x^5 + 1 |
|
|
26 |
x^12 – x^11 +
x^10 – x^9 + x^8 – x^7 + x^6 – x^5 + x^4 – x^3 + x^2 – x + 1 |
|
|
27 |
x^18 + x^9 + 1 |
|
|
28 |
x^12 – x^10 + x^8
– x^6 + x^4 – x^2 + 1 |
|
|
29 |
1 + x + x^3 + x^4
+ x^2 + x^6 + x^5 + x^10 + x^9 + x^8 + x^7 + x^12 + x^11 + x^16 + x^15 + x^14
+ x^13 + x^18 + x^17 + x^22 + x^21 + x^20 + x^19 + x^28 + x^26 + x^27 + x^25
+ x^24 + x^23 |
|
|
30 |
x^8 + x^7 – x^5 –
x^4 – x^3 + x + 1 |
|
![]()
|
Retour Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()