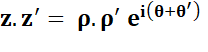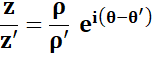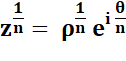NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/06/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Nombres complexes
Débutants Complexes	Formes			Glossaire Complexe
INDEX Complexes		Cartésien	Polaire	Exponentiel
		Matrice
		Sommaire de cette page >>> Forme exponentielle >>> Opérations >>> Logarithme complexe

Nombres complexes

Forme exponentielle

Forme exponentielle
La forme polaire La forme exponentielle	Rhô est le module et Thêta est l'argument.
Formules d'Euler qui montrent le passage du polaire à l'exponentielle et réciproquement.

Opérations
Si les opérations, additions et soustractions, des nombres complexes sont simples en utilisant la forme cartésienne, ce sont les opérations plus compliquées qui deviennent simples sous le format exponentiel (vrai aussi en polaire): multiplication, division, puissance, racine.
Multiplication Division Rappel De Moivre Puissance Racine

Logarithme complexe
Exemples

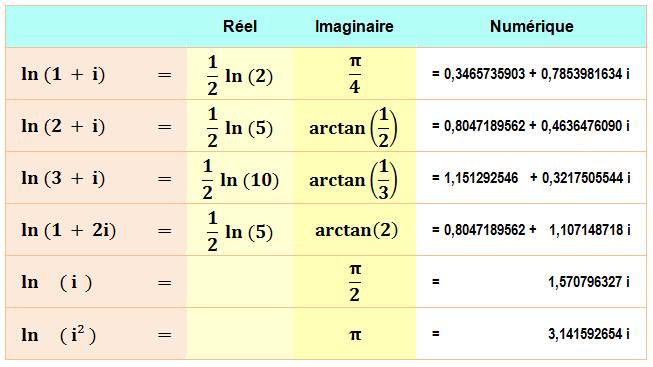
Voir Puissance de l'imaginaire / Exponentielle imaginaire / Formule d'Euler

Suite	Nombres complexes – Index Forme matricielle Opérations
Voir	Constantes Inventaire des types de nombres Nombres – Glossaire et index Nombres réels Opérations – Index Vecteurs
Cette page	http://diconombre.fr/Wwwgvmm/Type/aaaCompl/Exponent.htm