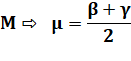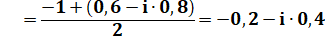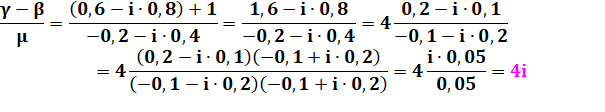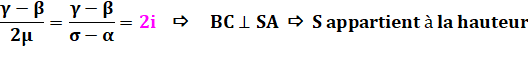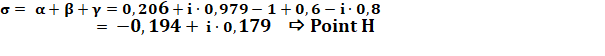Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 01/11/2020 M'écrire Brèves de Maths

INDEX Types de triangles Triangle Géométrie	Triangle: Droites remarquables
	Droites et points	Bissectrices	Hauteurs – Propriétés
	Point Milieu	Médianes	Hauteurs – Démo
	Point et triangles	Médiatrices	Hauteurs – Démo-suite
	Distances

HAUTEURS du TRIANGLE (3/3) Propriétés des hauteurs du triangle. Suite des démonstrations sur l'orthocentre. Occasion de découvrir de nombreuses propriétés des hauteurs des triangles.
	Sommaire de cette page >>> Démo avec quadrilatères inscriptibles >>> Démo avec les bissectrices >>> Démonstration la hauteur symétrique >>> Démonstration la parallèle à la hauteur >>> Démo avec vecteurs >>> Démonstration avec nombres complexes	Débutants Géométrie Glossaire Hauteur

Voir Propriétés fondamentales des triangles

Démonstration avec quadrilatères inscriptibles		haut
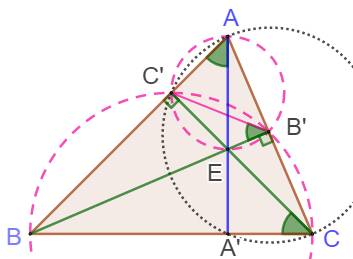
Démonstration – Inscriptible / Cocycliques Le triangle ABC et ses deux hauteurs BB' et CC' qui se coupent en E. Il s'agit de montrer que AE est perpendiculaire à BC et constitue la troisième hauteur. Avec la présence d'angles droits, les quadrilatères BCB'C' et AB'EC' sont inscriptibles (BC est le diamètre de l'un des cercles et AE celui de l'autre). Les angles en vert qui, deux à deux, interceptent des arcs égaux sont égaux. Avec l'égalité des angles en A et C, le quadrilatère ACA'C' est inscriptible lui aussi (petits pointillés). L'angle en C' est droit (AC est le diamètre de ce cercle), alors l'angle en A' est droit lui aussi. Réciproque Si AA', BB' et CC' sont les céviennes du triangle ABC se coupant en E et si les quadrilatères AC′EB′ and C′B′CB sont inscriptibles, alors E est l'orthocentre du triangle.	Propriété Si deux quadrilatères parmi les six (AC′EB′; BA′EC′; CB′EA′; C′B′CB; A′C′AC; B′A′BA) sont inscriptibles, alors ils le sont tous et E est l'orthocentre du triangle.

Voir Propriétés des angles

Démonstration avec les bissectrices		haut
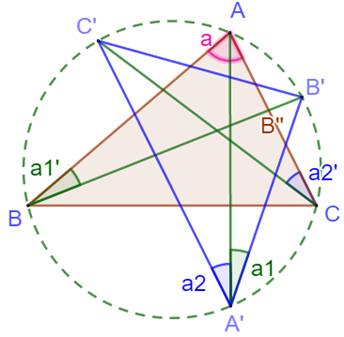
Démonstration – Bissectrices (1) Le triangle ABC et son cercle circonscrit Les trois hauteurs en vert supposées non concourantes sont prolongées et rencontrent le cercle en A', B' et C'. Les angles a1 et a1' qui interceptent le même arc sont égaux. Or a1' = 90° – a (dans le triangle rectangle ABB'') Les angles a2 et a2' qui interceptent le même arc sont égaux. Or a2' = 90° – a. Les angles a1 et a2 sont égaux et AA' est la bissectrice de l'angle en A'. Même chose pour BB' et CC', bissectrices des autres angles du triangle A'B'C'. Or les bissectrices se coupent en un point unique. Ces bissectrices sont aussi les hauteurs du triangle ABC. Celles-ci se coupent donc en un point unique.	L'orthocentre de ABC est aussi le centre du cercle inscrit au triangle A'B'C' (empreinte des hauteurs sur le cercle circonscrit).
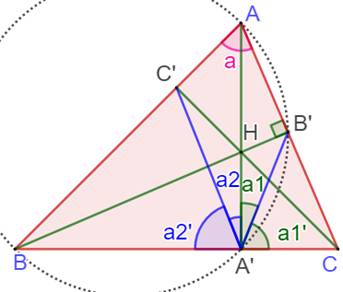
Démonstration – Bissectrices (2) Le triangle ABC et son cercle circonscrit Les trois hauteurs en vert. H est l'intersection de AA' et BB'. La troisième CC' est supposée non concourante. On veut montrer que AA' est la bissectrice de l'angle B'A'C', que a1 = a2. Les points AB'A'B sont cocycliques (triangles rectangles AB'B et AA'B). L'angle a1' est supplémentaire de BA'B' qui est supplémentaire de l'angle a. A1' = a a1 = 90° – a1' = 90° – a De même avec le quadrilatère inscriptible ACA'C': a2 = 90° – a2' = 90° – a AA' est la bissectrice de l'angle BA'C'; de même pour les deux autres. Or les bissectrices se coupent en un seul point. Comme ce sont les hauteurs du triangle ABC, celles-ci se coupent un point unique.	L'orthocentre de ABC est aussi le centre du cercle inscrit au triangle A'B'C' (pieds des hauteurs).

Démonstration la hauteur symétrique		haut
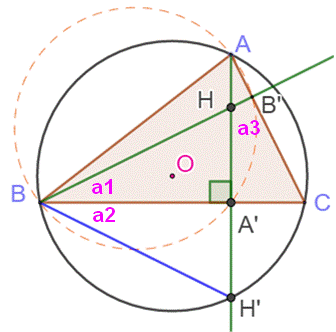
Démonstration – tracé d'une hauteur symétrique Triangle ABC et son cercle circonscrit. Hauteur AA' prolongée qui coupe le cercle en H' On positionne un point H sur AA' tel que A'H = A'H'. (vous le devinez BH est une hauteur; elle est symétrique de BH' par rapport au côté BC). Par construction, les angles: a1 = a2. Interceptant le même arc CH': a2 = a3 Les angles égaux a1 et a3 interceptent le même arc A'B'. Les points ABA'B' sont cocycliques. Interceptant le même arc AB, les angles en A et en B' sont égaux et valent un angle droit. Le segment BB' est bien une hauteur. Le même raisonnement tient pour la hauteur issue de C.

Démonstration avec la parallèle à la hauteur		haut
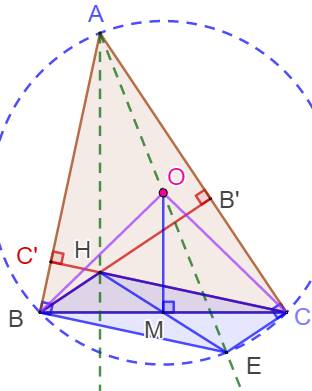
Parallélogramme avec les hauteurs Triangle ABC et son cercle circonscrit. Le point E diamétralement opposé à A. Le quadrilatère BECH (bleu) est un parallélogramme. M est le point milieu des diagonales. Avec OB = OC = R, le triangle OBC est isocèle en O et sa médiane OM est aussi sa médiatrice. OM est perpendiculaire à BC. Dans le triangle AHE, O et M sont des points milieux. OM est parallèle à AH et AH est donc perpendiculaire à BC comme OM. Finalement, AH est bien une hauteur du triangle ABC et elle passe par H, intersection des deux autres hauteurs.

On trouve cette démonstration dans le pdf de Daniel PERRIN

Démonstration avec vecteurs		haut
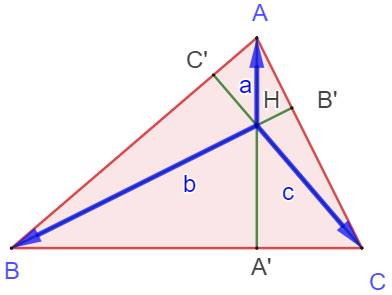
Les hauteurs AA' et BB' se coupe en H. Il faut démontrer que la droite CC' est perpendiculaire à AB. On note les vecteurs: Traduction de HA perpendiculaire à BC: Traduction de HB perpendiculaire à AC: En ajoutant les deux égalités et en développant: Cette relation veut dire que OC est perpendiculaire à AB. Les trois hauteurs sont concourantes.	Rappel

Démonstration avec nombres complexes		haut
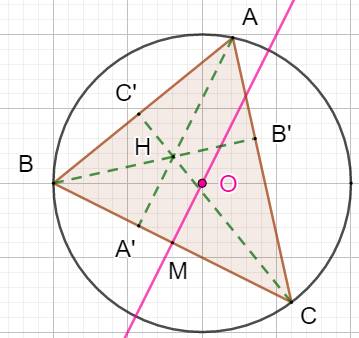
Le cercle trigonométrique est le cercle circonscrit au triangle ABC. La démo est immédiate. Je donne une application numérique pour faciliter la compréhension. Lecture des coordonnées sur la figure Voir Nombres complexes Démonstration Les points A, B et C sont donnés. Le point M est le milieu de BC. Nommons S le point suivant: OM est la médiatrice, elle est perpendiculaire à BC, alors, la quantité suivante est purement imaginaire:	Complexes et orthogonalité
En remplaçant mu: Même raisonnement pour les autres côtés. S est l'orthocentre H. Vérification numérique

Haut de page

Retour	Hauteurs du triangle (1/3) Démonstrations (2/3)
Suite	Médianes Droites et points Droite d'Euler Droite de Simson
Voir	Triangle – Index Triangle – Glossaire Éléments de géométrie Triangle – Débutants, novices DicoMot DicoNombre
Sites	Le concours des hauteurs d’un triangle – Daniel PERRIN – Université Paris Saclay Proof that the Altitudes of a Triangle are Concurrent – The University of Georgia Concurrency of the Altitudes of a Triangle – Mowaffaq Hajja and Horst Martini
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/Hauteur2.htm