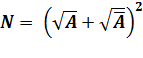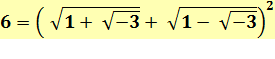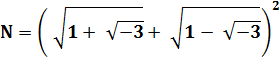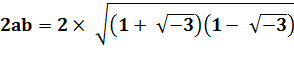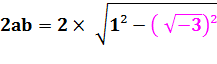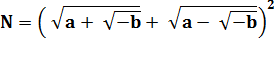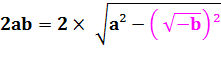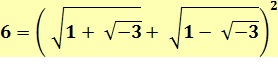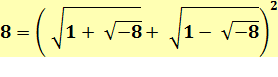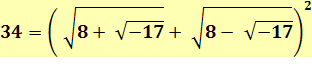NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/05/2014 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Types de NOMBRES
Débutants Complexe	NOMBRES COMPLEXES Réels		Glossaire Complexe
INDEX Complexes		Puissances entières	Conjugués entiers
		Sommaire de cette page >>> Calcul avec exemple >>> Généralisation >>> Table

Somme des racines des CONJUGUÉS

Nombres de la forme:

Exemple:

Relation avec les racines de nombres négatifs trouvée par Leibniz.

Voir Liste des nombres irrationnels

Calcul pas à pas avec l'exemple donné
Calculons le carré de la somme des conjugués:
Avec (a + b )² = a² + b² + 2ab
Cas du double produit avec et (a + b) (a – b) = a² – b²
Somme	N = 2 + 4 = 6

Généralisation
Expression générale
Condition d'obtention d'un nombre entier: 2ab doit être entier.
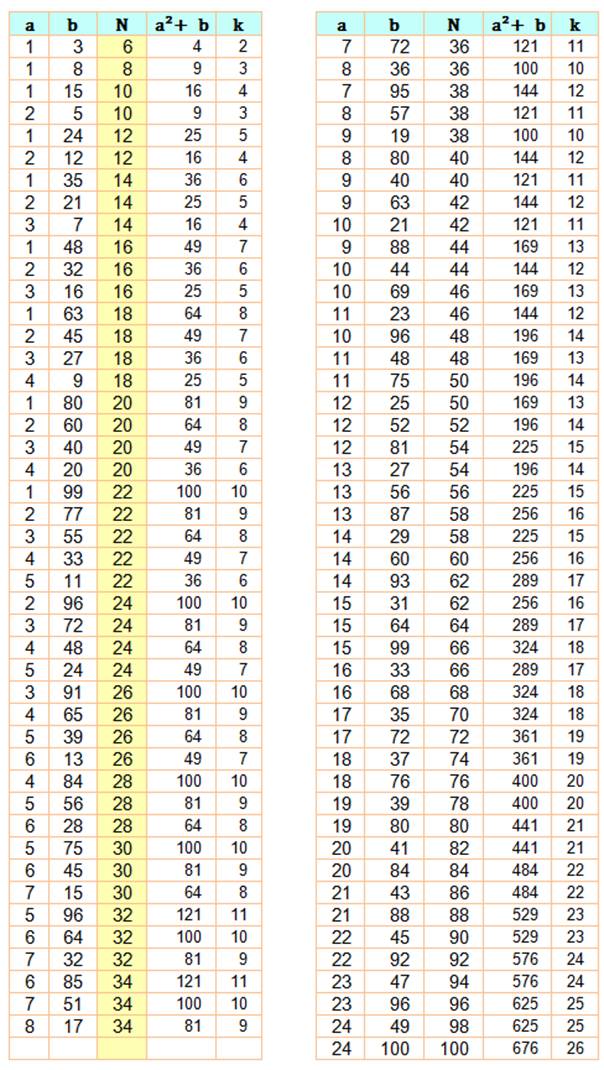
Le nombre obtenu vaut: Ce nombre est toujours pair.	N = 2a + 2k = 2(a+k)
Exemples	a = 1 et b = 3 => k² = 1² + 3 = 4 et N = 2 x (1+2) = 6
	a = 1 et b = 8 => k² = 1² + 8 = 9 et N = 2 x (1+3) = 8

Table
Toutes les valeurs pour a, b et N jusqu'à 100. Exemple (dernière ligne à gauche): a = 8 et b = 17 => k² = 8² + 17 = 81 = 9² et N = 2 x (8+9) = 34

Suite	Complexes Formule de Bombelli Complexe – Index
Voir	Types de nombres
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/ConjEnt.htm