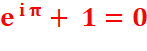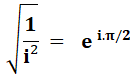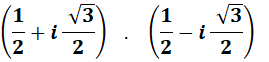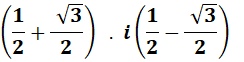Orientation Glossaire	Atlas / Nombres / Nomenclature des nombres
Débutant DicoMot DicoNombre	Nombres IMAGINAIRES Nombres COMPLEXES

Approche

Nombre IMAGINAIRE

Invention abstraite de mathématiciens.

En fait, un outil- levier pour résoudre des problèmes.

Comme un échafaudage qui aide à monter une construction et qui, en disparaissant, laisse voir la beauté de l'édifice.

Voir comment les mathématiciens n'hésitent pas à passer dans un monde parallèle pour disposer d'un levier mathématique.

Nous savons que la racine carrée de l'unité

est 1, car 1 x 1 = 1

c'est aussi –1 car (–1) x (–1) = 1.

La création des nombres imaginaires résulte de la recherche d'une racine carrée à –1.

Elle n'existe pas dans le monde des nombres réels: aucun nombre multiplié par lui-même ne donne –1.

Cette racine, notée i, fait partie d'un nouveau monde, celui des nombres imaginaires.

Par conséquent et par définition, chez les imaginaires: i² = –1.

	Réel	Imaginaire
Nombre	1	– 1
Racine positive	1	i
Racine négative	– 1	– i

Nombre COMPLEXE

Nombre, noté z, comprenant:

une partie réelle (a), et

une ou plusieurs parties imaginaires (b, c …).

Typiquement: z = a + i . b

Avec a et b des nombres réels

et i le nombre imaginaire de base, ou unité imaginaire.

Exemple: (a + 12) + (a – 5) i

Partie réelle : a + 12

Partie imaginaire: a – 5

Intérêt

S'agissant de la résolution des équations en général: Nous sommes heureux lorsque nous en trouvons les racines; Par contre, nous ne savons pas quoi faire lorsqu'elles n'existent pas. Elles semblent là, derrière l'équation, repliées dans les nombres, sans que l'on puisse les extraire. Il suffirait théoriquement d'appliquer la méthode générale. Mais, nous butons sur l'extraction de racines négatives … Avec la race des nombres complexes: Nous disposons d'un outil qui permet de révéler cette latente. En effet, dans le monde des complexes, il y a toujours des solutions! On y retrouve nos valeurs réelles, si elles existent. PLUS des valeurs complexes qui complètent le tableau: Deux racines pour toute équation du 2^e degré: ax^2 + bx + c = 0 Trois racines pour toute équation du 3^e degré: ax^3 + bx^2 + cx + d = 0 Quatre racines …

i

Le nombre imaginaire i est la racine de l'équation: x² + 1 = 0 Valeur de i = –1 et i² = –1.

Définitions	Nombre complexe Nombre de la forme: z = a + i . b avec (a, b) R² (Lire: a et b sont deux nombres réels), et i = ( i est égal à racine de -1, ou x est racine de x² + 1 = 0). Réel et imaginaire La partie réelle s'écrit Re(z) = a La partie imaginaire s'écrit Im(z) = b Si b = 0, le nombre est réel (pur). Si a = 0, le nombre est imaginaire pur.
Interprétation	Représentation géométrique du nombre complexe Le complexe z = a + ib est appelé affixe du point M de coordonnées (a, b). Voir Cartésien et polaire

Égalité	Deux nombres complexes (a + ib) et (c+ id) sont égaux si et seulement si a = c et b = d
Conjugué	Le nombre complexe z* = a – ib est le conjugué de z = a + ib Avec cette propriété: z . z* = (a + ib) (a – ib) = a² – (ib)² = a² – i²b² = a² + b² Notation: Le conjugué est noté z surligné ou z* lorsqu'on ne peut pas faire autrement: z = a + ib = z* = a – ib
Module & Argument	Module ou valeur absolue d'un nombre complexe Noté , lire ro: Exemple: 3 + 4i = Cette valeur est la longueur de l'hypoténuse d'un triangle rectangle dont les côtés mesurent a et b. Dans cette figure, l'angle formé par le côté a et l'hypoténuse est appelé l'argument du nombre complexe, il noté (lire thêta). Un nombre complexe est complètement caractérisé par: son module - longueur de l'hypoténuse, et son argument - angle.

Formes	Les trois écritures équivalentes d'un nombre complexe: Forme algébrique: z = a + i . b Forme polaire: z = (cos + i sin ) Forme exponentielle: z =
Formule célèbre		Formule d'Euler impliquant pas moins que cinq nombres remarquables 0, 1, e , i et

English

Imaginary number, complex number. We can consider a complex number as having the form z = a + ib where a and b are real numbers and i, which is called the imaginary unit, has the property that i² = – 1. A number of the form a + ib where a, b R, the set of real number, and i = –1, is called a complex number A complex number is said to be purely real if I(z) = 0 and purely imaginary if R(z) = 0. The conjugate of the complex number z = a + ib is defined to be a – ib and is denoted by z* (or better, z above-scored ).

Suite	Nombres complexes – Index Introduction aux nombres complexes Le vocabulaire des nombres complexes Racines nièmes de l'unité – Polynômes cyclotomiques Nombres complexes j et j*
Autres	Abécédaire du débutant 1 = 2 Démonstration fausse avec les nombres complexes Calculs avec les nombres complexes Complexité – Concept des sciences d'aujourd'hui Constantes Équation du deuxième degré Équation du troisième degré Exercices du baccalauréat 2018 Fractales ou la beauté des complexes en images Identités remarquables avec les complexes Nombres entiers, réels et complexes Nomenclature des nombres Octonions de Cayley Puissance de l'imaginaire - i puissance i Quaternions de Hamilton Table de multiplication du 1 étendu à i Un, moins un et i
Voir aussi	Fractales ou la beauté des complexes en images Complexité – Concept des sciences d'aujourd'hui Complications des montres
Cette page	http://villemin.gerard.free.fr/Referenc/Vocabula/GlosI/Imaginai.htm

Nombres ENTIERS, RÉELS & COMPLEXES

	= – i	>>>
	= i	>>>
	= –1 = –1	>>>
+ 1	= 0	>>>
	= 0,207 …	>>>
	= 0,707 + 0,707 i	>>>
	= 1 + i =	>>>
– i² = i ^4 =	= 1	>>>
	= 1 = 1	>>>
	= 0,5 i
(1 + i) + (1 – i) (1 + i) . (1 – i)	= 2 = 2	>>>
(n + i) . (n – i) (n + m.i) . (n – m.i)	= n² + 1 = n² + m²	>>>

CALCUL avec les COMPLEXES

Opérations

Addition	(a + ib) + (a' + ib')	= (a + a') + i (b + b')
Soustraction	(a + ib) – (a' + ib')	= (a – a') + i (b – b')
Multiplication	(a + ib) . (a' + ib')	= aa' + aib' + iba' + i²bb'
		= (aa' – bb') + i (ab' + a'b)

Division avec a ou a' 0	(a + ib)	=	(a + ib) (a' – ib')	=	aa' + bb' + i (a'b – ab')
	(a' + ib')		(a' + ib') (a' – ib')		a'² + b'²

Utilisation du conjugué

Inverse avec a 0	1	=	(1) (a – ib)	=	a – ib
	(a + ib)		(a + ib) (a – ib)		a² + b²

Formule de De Moivre

Formule avec n entier ou rationnel

( cos + i sin )^n

= cos (n) + i sin (n)

Calculs divers

Conjugué	z + z*	= 2 a	= 2 Re(z)
	z – z*	= 2 b	= 2 Im (z)
	z . z*	= a² + b²	= z²

Module	z= - z	= z*= – z*
	z1 + z2	z1+ z2
	z1 . z2	= z1.z2
	z1 + z2²	= z1² + z2² + 2 Re(z1 . z2*)
	z1 + z2² + z1 – z2²	= 2z1² + 2z2²

Argument	( z1 . z2)	= ( z1) + ( z2)
	( z1 / z2)	= ( z1) – ( z2)

Voir Vocabulaire associé aux nombres complexes