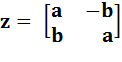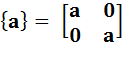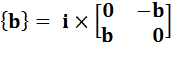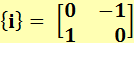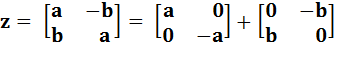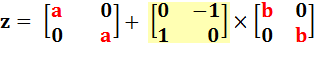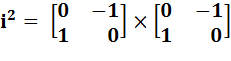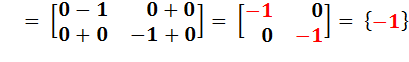|
||||||||||||||||||||||||||
![]()
|
Nombres complexes Forme matricielle La
commission Lichnérowicz (1966-1973) a choisi la matrice carrée d'ordre deux
pour définir les nombres complexes. Avantages:
des propriétés des matrices découlent implicitement les propriétés des
nombres complexes. L'utilisation géométrique des nombres complexes sont aussi
celle des matrices en matière de similitudes et de rotation. |
André Lichnérowicz (1915-1998), mathématicien français
|
|
||
|
|
|
|
|
|
||
|
|
|
|
z =
a
+ i b
|
|
Voir Multiplication des matrices
|
Calcul de i² |
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()