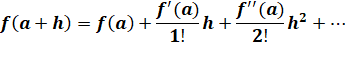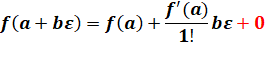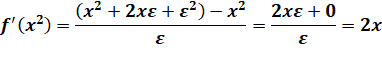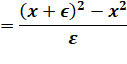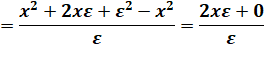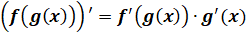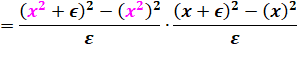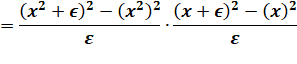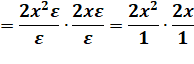Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 01/12/2024 M'écrire Brèves de Maths

INDEX Complexes Type de Nombres Débutants	Types de Nombres en doublets
	Nombres complexes	Nombres duaux

Faites un double-clic pour un retour en haut de page

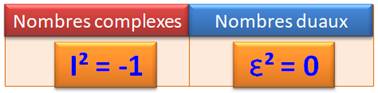
NOMBRES DUAUX Les nombres duaux sont les cousins des nombres complexes: au lieu de i² = 1 , on y trouve ε² = 0. Un artifice mathématique qui, en considérant la quantité infinitésimale ε, simplifie les calculs notamment de dérivation ou encore les calculs d'angles dans l'espace. Aussi, utilisés en mécanique quantique. Cette page est une introduction aux nombres duaux. Pour plus, se reporter aux références indiquées et aux articles universitaires.
	Sommaire de cette page >>> Présentation des nombres duaux >>> Historique et applications >>> Comparaison >>> Série de Taylor et différentiation >>> Calcul de dérivées	Débutants Nombres Glossaire Nombres

Présentation des nombres duaux		haut
Présentation mathématique En mathématiques et en algèbre abstraite, les nombres duaux sont une algèbre associative unitaire commutative à deux dimensions sur les nombres réels, apparaissant à partir des réels par adjonction d'un nouvel élément ε Et cela, avec la propriété ε² = 0, ε étant un élément nilpotent. Les nombres duaux sont un exemple d'anneau qui possède un élément nilpotent non nul.	Décodage Les nombres duaux, comme les nombres complexes, sont composés de deux nombres, l'un réel et l'autre spécial: Pour les complexes: a + i b avec i² = 1 Pour les duaux: a + ε b avec ε² = 0 et ε ≠ 0 => ε / ε = 1 Les opérations arithmétiques classiques (additions, multiplications) sont réalisables sur l'ensemble des nombres duaux, comme sur l'ensemble des nombres complexes, comme sur l'ensemble des nombres réels ou entiers. Le truc ! L'astuce consiste à approcher le zéro par une entité ultra petite (ε) tout en posant que son carré (évidemment encore plus petit) est nul (en fait, ignoré et posé comme nul par définition). Cependant ε n'est pas nul et peut être utilisé pour diviser.
Coin maths En un certain sens, les nombres duaux peuvent être conçus comme des doublets de nombres réels munis de certaines lois de composition interne. Définition Un anneau commutatif R est dit être un anneau commutatif dual général si chaque élément de R est de la forme a + bε où a, b ∈ R et ε est un nouvel élément (nombre non réel) tel que ε² = (0) et ce ε est unique et ε lui-même n'est pas nul. Anneau commutatif veut dire qu'il s'agit en particulier d'un ensemble R² muni des lois d'addition et de multiplication sur les couples de nombres réels, définies respectivement par: (a , b) + (c , d) = (a + c , b = d) (a , b) ٠ (c , d) = (a٠c ,, a٠d + b٠c) La multiplication est commutative, associative et distributive sur l'addition.

Historique et applications		haut
Historique Les nombres duaux ont été introduits par William Clifford en 1873. Applications par A.P. Kotelnikov en 1895. Utilisés au début du XX^e siècle par le mathématicien allemand Eduard Study qui s'en servit pour calculer l'angle entre droites dans l'espace. Une généralisation fut définie par Hermann Grasmann à la fin du XIX^e siècle. McAulay a utilisé des quaternions duaux pour décrire le déplacement fini d'éléments rigides et déformables. William Kingdon Clifford (1845-1879 / 34 ans) Mathématicien et philosophe anglais inventeur des nombres duaux. Connu aussi pour sa théorie des graphes. Ses idées pionnières sur la théorie de l'espace de la matière ont joué un rôle important dans le développement de la théorie de la relativité par Albert Einstein.	Applications Outil de dérivation automatique >>> Calcul d'angles: la partie réelle est un angle et la partie duale est une longueur. Applications en mathématiques: combinaisons de rotations et de translations; transformation de coordonnées sphériques en coordonnées cylindriques; etc. Applications en mécanique: systèmes de vis, modélisation de joints plans, méthodes itératives pour l'analyse des déplacements de mécanismes spatiaux, analyse des forces d'inertie de mécanismes spatiaux, etc. Applications en physique quantique: la direction le long de ε s'appelle la direction fermionique, et la composante réelle est appelée la direction bosonique.

Comparaison		haut
Nombres complexes	Nombres duaux
Deux nombres associés avec i² = -1 sous la forme: z = a + ib a = Re(z) partie réelle b = Im(z) partie imaginaire	Deux nombres associés avec ε² = 0 sous la forme: z = a + εb a = Re(z) partie réelle b = Du(z) partie duale
	La partie duale, du fait de la multiplication par epsilon, est une quantité infinitésimale.
Un nombre complexe peut être représenté par un vecteur dans le plan complexe. La multiplication complexe peut être considérée comme une mise à l'échelle et une rotation d'un vecteur par la grandeur et l'argument d'un autre, respectivement.	Les nombres duaux illustrent le principe d'invariance de Galilée (relativité des mouvements). La partie infinitésimale d'un nombre dual représente la vitesse.
Addition (a + bi) + (c + di) = (a + c) + (b + d)i Soustraction (a + bi) – (c + di) = (a – c) + (b – d)i	Addition (a + bε) + (c + dε) = (a + c) + (b + d)ε Soustraction (a + bε) – (c + dε) = (a – c) + (b – d)ε
Multiplication (a + bi) (c + di) = (ac – bd) + (ad + bc) i Le produit des deux nombres imaginaires b et c devient réel.	Multiplication (a + bε) (c + dε) = (ac + 0) + (ad + bc)ε Le produit des deux nombres duaux b et c ne devient pas réel; La part réelle est indépendante des parts duales; et La part duale de la multiplication est un produit croisé réel-dual.

Série de Taylor et différentiation		haut
Toute valeur de f(a + h) d'une fonction continue f peut être exprimée par une somme infinie où f', f'' … désigne les dérivées première, deuxième, … de la fonction f.
Expression dans le monde dual. Alors, tous les termes sauf le premier, sont nuls.
Toute fonction réelle différentiable peut se voir sous l'angle dual.
Exemple 1
Exemple 2: Différentiation automatique de: f = x² Rappel: ε² = 0. La méthode consiste à prendre b = 1.

Calcul de dérivées		haut
Exemple avec f'(x²)
On se souvient que ε² = 0; ε ≠ 0 => ε / ε = 1
On retrouve la valeur connue
Exemple de la dérivée d'une composition de fonctions.
Prenons: f(x) = g(x) = x²
Attention à ne pas multiplier les epsilons trop tôt, sinon on aurait 0 / 0 !
On retrouve la dérivée de x^4

Voir Dérivées / Dérivées usuelles

Merci à Frédéric Bonnard pour l'idée de cette page

Haut de page (ou double-clic)

Suite	Nombres imaginaires Nombres complexes – Index
Voir	Types de nombres Infinitésimaux
Sites	Éléments de la représentation duale – Cours Fondements mathématiques – Jean Hladik et Pierre-Emmaule Hladik The dual numbers – John Mount – Vidéo Programming with Dual Numbers and its Applications in Mechanisms Design – Dr Harry et H. Cheng – Avec rappel historique
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Type/aaaCompl/NbDuaux.htm