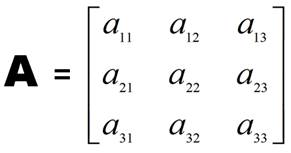NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/11/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	OUTILS
Débutants MATRICE	MATRICES				Glossaire Général
INDEX Matrices Outils	Introduction	Addition	Multiplication	Puissance
	Formes	Déterminant	Inversion	Historique
		Sommaire de cette page >>> Approche >>> Applications >>> Définition >>> English corner

MATRICES – Introduction

TABLEAU de nombres qui devient un objet mathématique avec ses propriétés propres

Voir Débutants / Novices

APPROCHE

Il est parfois plus simple de faire un tableau plutôt qu'une énumération.

Dans ce cas, le tableau avec ses lignes et colonnes est pratique pour effectuer des sommes, des statistiques.

Données

Famille A: 2 adultes, 1 garçon et 1 fille

Famille B: 2 adultes, 3 garçons et 1 fille

Famille C: 1 adulte, 0 garçon et 1 fille

Famille D: 4 adultes, 2 garçons et 4 filles

Mise en tableau

	Adultes	Garçons	Filles
A	2	1	1
B	2	3	1
C	1	0	1
D	4	2	4

Tableau des compositions familiales

Il est des cas où ce tableau représente des valeurs liées entre-elles.

Le tableau de nombres devient un objet mathématique à part entière, une matrice.

Comme un simple nombre, ce tableau, dispose de propriétés arithmétiques, précieuses pour effectuer des calculs globalement et systématiquement.

Données

5x + 3y – 5z + 21 = 0

8x + 6y + 2z – 4 = 0

2x – 4y – 3z + 2 = 0

Mise en tableau

5	3	- 5	21
8	6	2	- 4
2	- 4	- 3	2

Matrice du système d'équations

Résolution par la méthode des déterminants

Les matrices sont un outil mathématique

Elles forment des entités globales, disposant de propriétés propres et de règles de calcul.

Elles sont pratiques car elles donnent le moyen d'effectuer des opérations sur des tableaux de nombres, chacun considéré comme un objet (analogie avec le langage objet en programmation).

Une fois adoptées, il est inutiles de re-décrire les opérations élémentaires à chaque fois que l'on utilise de tels tableaux de nombres.

APPLICATIONS
Résolution des systèmes d'équations linéaires. Changement d'axes dans l'espace, images calculées en 3D. Et, d'une manière générale, transformation géométriques: translation, rotation, symétrie … Calculs sur les nombres hypercomplexes Application à la résolution de graphes (recensement du nombre d'arêtes sur un sommet). Mécanique quantique Etc. Plus généralement, les matrices permettent une systématisation d'opérations qui se prêtent facilement au calcul automatique (algorithmique)	Illustration (purement indicative) Extrait de Virtual Reality – John Vince – Pearson Education – 1995

DÉFINITIONS
Matrice à n lignes et p colonnes Usuel Tableau rectangulaire de nombres disposés suivant n lignes et p colonnes, n et p pouvant être égaux (matrice carrée) Maths (pour initiés) 1) On appelle matrice à n lignes et p colonnes, possédants n x p éléments (ou coefficients) dans K, une application de (1, ... , n) x (1, … , p) dans K 2) Soient n et p deux entiers naturels non nuls et les ensembles I = {1, 2, …, n} et J = {1, 2, …, p}. On appelle matrice à n lignes et p colonnes à éléments dans un corps commutatif K ou matrice (n,p) une application M de I x J dans K L'image du couple (i,j) se note aij et s'appelle un élément de la matrice M (Selon Dictionnaire des mathématiques – puf) Matrices particulières Matrice colonne:(ou vecteur-colonne ou unicolonne) si p = 1 Matrice ligne (ou vecteur-ligne ou uniligne) si n = 1 Matrice carrée: Si même quantité de lignes et de colonnes (n= p). C'est une matrice d'ordre n Les éléments en aii forment la diagonale Il existe 3 matrices carrées d'ordre 2 et 45360 d'ordre 3 Autres >>>	Notation A = (aij) Représentation par un tableau bordé par deux segments (droit parfois courbes) Dénominations Matrice à n lignes et p colonnes n et p sont les dimensions de la matrice Formée des éléments (termes ou coefficients) ai j Matrice de dimension, taille ou format (n,p) Voir Déterminants NB La matrice est notée en lettre majuscule; ses éléments en minuscules, doublement indexés

Notation des lignes et colonnes

Le premier indice donne le numéro de la ligne ou rangée (row).

Le second indique le numéro de la colonne (column).

Notez le moyen mnémotechnique en prenant la troisième notation: Arc

ENGLISH CORNER
A matrix is an ordered set of numbers listed rectangular form. With a matrix having three rows and four columns, we say it is a 3 x 4 matrix We denote the element on the i row and j column with a i,j If a matrix has n rows and n columns then we say it's a square matrix	A matrix, several matrices Row; Row-matrix Column; Column-matrix Square matrix Diagonal matrix Identity matrix Determinant The transpose of a matrix The inverse of a matrix Simultaneous equations En anatomie La matrice au sens utérus se dit womb

MATRICES	Algorithme QR Exemple avec construction d'un rectangle magique Exemple: énigme du travail dans les champs Historique Matrices – Débutants Matrices et nombres complexes Méthode avec sous-espace de Krylov Somme de la diagonale Tenseurs Types de matrices Vecteurs – Débutants
Voir	Équations Outils mathématiques Tables Théorie des nombres
Sites	Matrice (mathématiques) - Wikipédia Matrice – Résumé des cours – BibM@th.net Matrix -- from Wolfram MathWorld
Cette page	http://villemin.gerard.free.fr/aMaths/Outils/Matrice/Intro.htm