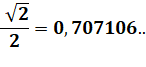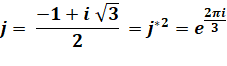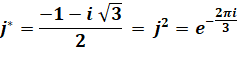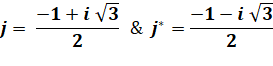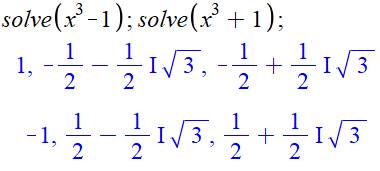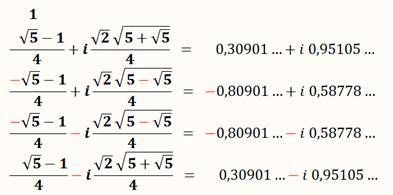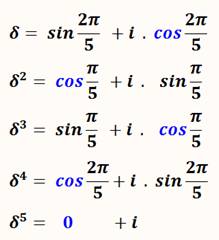|
||||||||||||||||||||||||||||||||
![]()
|
RACINES DE L'UNITÉ & Polynômes cyclotomiques Les nombres complexes sont
basés sur la racine carrée imaginaire de – 1. Ici, nous allons nous
intéresser à la racine nième de l'unité. Mais, les nombres imaginaires sont
toujours présents … |
Note: ![]() est l'ensemble des nombres complexes de module
1 (sur le cercle unité).
est l'ensemble des nombres complexes de module
1 (sur le cercle unité).
C'est le groupe des
unités de ![]() .
.
En bref

|
|
||
|
Principe
Nombre de De Moivre
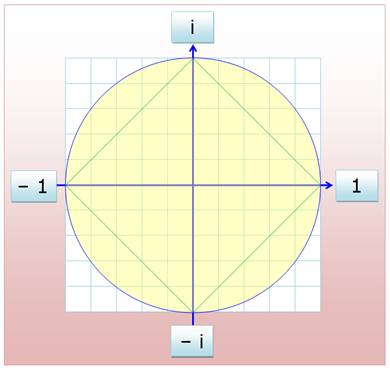
d4 = { 1, i, –1, –i } Équation
x²
– 1 = 0
x² + 1 = 0 |
|
|
|
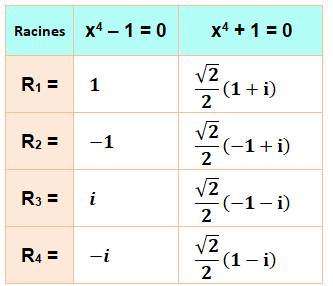
Racines
|
|
|
Voir Groupes
cycliques / Identités
remarquables / Nombre
0,707…
|
|
||
|
Principe
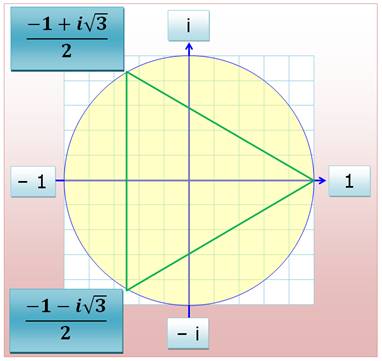
Triangle équilatéral
Nombre de De Moivre
d3
= {1, –0,5 + 0,5 |
|
|
|
z3
– 1 = 0 dont les racines sont:
Notez que chaque racine cubique
complexe est le carré de l'autre. |
Autre équation (cyclotomique) x²
+ x + 1 = 0 dont les racines sont:
j* est le conjugué
de j 1
+ j + j² = 0 La racine cubique j et parfois notée |
|
|
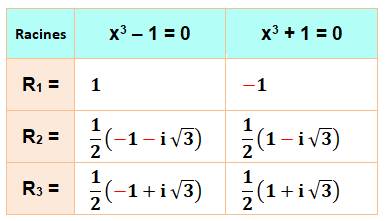
Conclusions 1.
La
recherche des racines cubiques de 1 donne trois valeurs dont deux imaginaires 2.
Le tracé
d'un triangle équilatéral
sur le cercle donne une représentation de ces racines 3. Il existe une équation, dite cyclotomique, dont
les racines sont les valeurs complexes de la racine de 1. Racines des deux équations
Calcul sous Maple
|
||
Voir Notations avec i et j (maths et électronique) / Résolution du
troisième degré / Exemple x3
– a = 0
|
Trouver les racines cubiques de l'unité |
|
|
|
Forme équivalente |
|
|
|
Équation à résoudre |
|
|
|
(x – 1) (x² + x + 1) = 0 |
||
|
Une racine évidente x = 1 |
|
|
|
Reste à résoudre |
|
|
|
|
||
|
Avec: a = b = c = 1 |
|
|
|
Deux nouvelles racines |
|
|
|
Deux racines conjuguées |
|
|
|
Valeurs numériques |
|
|
|
Pour information, la factorisation devient |
|
|
|
|
||
|
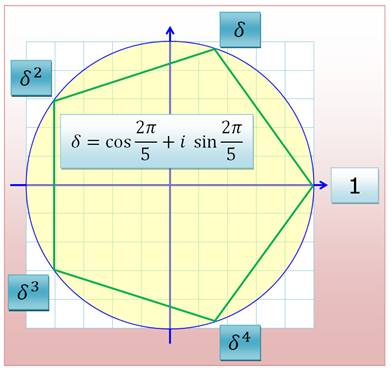
Principe
Attention, cela se complique! Nombre de De Moivre
Ce sont les racines de z5 = 1: Équation cyclotomique
d4
+ d3 + d2 + d + 1 = 0 |
|
|
Voir Solution des
équations quintiques
Voir Ordre 6
|
Il
est toujours possible de trouver n racine nième de l'unité en faisant appel
aux nombres complexes. La notation en sinus et cosinus est parfois commode pour
exprimer ces valeurs complexes. Voir
la suite en résolution générale de zn = 1 >>>
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()