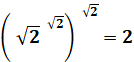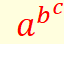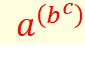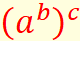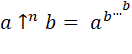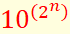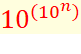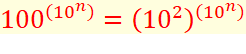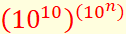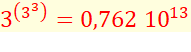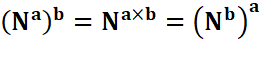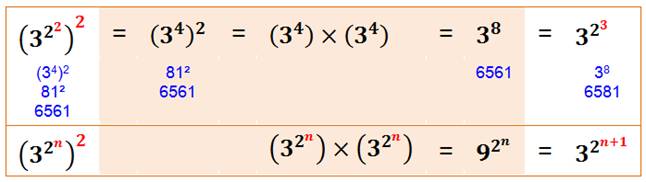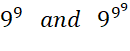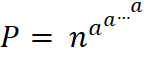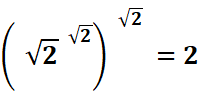|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Puissances
de puissances ou Exposants
à étages Calculs
et comparaison entre eux. |
English: tower power, hard
powers
Règle des
exposants à étage
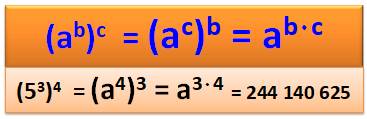
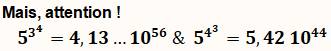
Voir Résoudre
x en puissance / Défis en algèbre
Exemple en apéritif (énigme classique sur le Net)

![]()
|
|
||
|
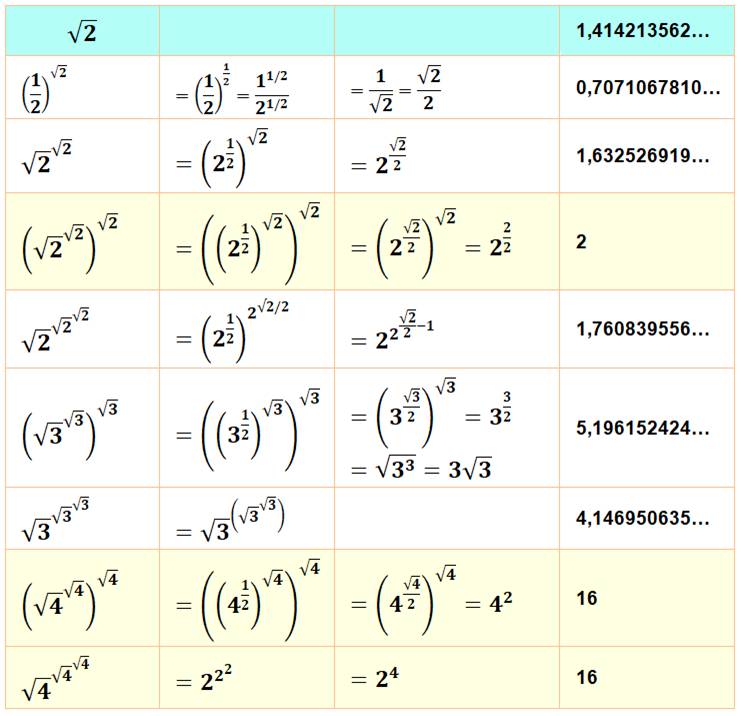
De cet exemple, l'on pourrait
conclure que l'ordre des parenthèses est indifférent sur le résultat.
Le mieux est de systématiquement
préciser les parenthèses, même s'il est permis de l'éviter dans le dernier
cas. La convention veut que l'on commence à calculer les puissances par les
exposants les plus hauts. |
|
|
Lecture des puissances à étages: ne pas confondre …
|
Calcul
des exposants par le haut ou, placer les parenthèses en haut. |
Loi
de composition des exposants ou,
on calcule d'abord dans les parenthèses. |
|
|
||
Voir irrationnels
produisant des rationnels Exploration
des racines à étages avec 2.
|
||
|
|
||
|
On mettrait 11 ans pour l'écrire à raison d'un chiffre
par seconde.
|
=
9 ^ 9 ^ 9 =
9 ^ (9 ^ 9) =
9 9 ^ 9 = 9 387 420 489 » 10 369 693
100 =
428 124 773 … 89 On ne connaît pas
les chiffres centraux. Pour mémoire 999 = 2,951… 1094 |
|
Suite en Grands nombres avec trois chiffres
/ Gogol
|
|
||||||||||||||||
|
NOTATION: Exposant versus
« Chapeau » des ordinateurs Le chapeau (accent circonflexe) permet une écriture
linéaire, sans superposition des exposants.
Notation de Knuth
Voir Notation
de Knuth |
||||||||||||||||
Voir Tétration
(cas où b = a)
|
|
||||||||||||||||||||||||||||||||||||||||
|
Exemples de calculs
Avec des 3 – Notez la progression fulgurante
Notez l’égalité générale
Ou en notation avec exposants à étages
|
||||||||||||||||||||||||||||||||||||||||
Voir Trois et cubes
|
|
|
|
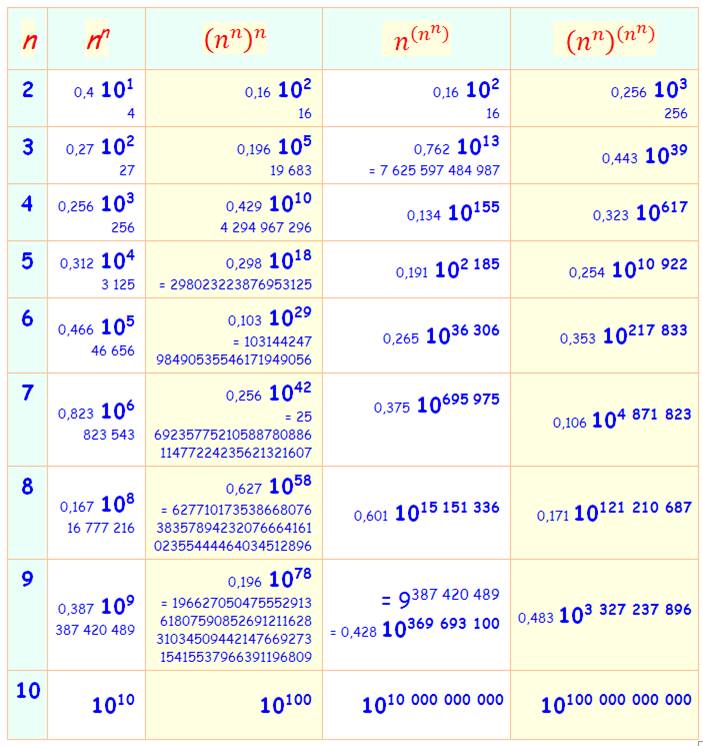
Valeur des puissances de dix selon les
exposants
|
|
Voir Puissances
de dix
|
|
|
|
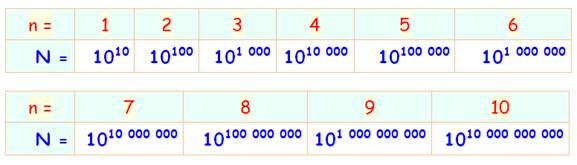
Nombre à une puissance, chacun de ces nombres étant
élevé à une puissance. Un passage par les logarithmes (décimaux) permet de se
rassurer. Exemple de lecture du
tableau avec k = 2 et N = 10².
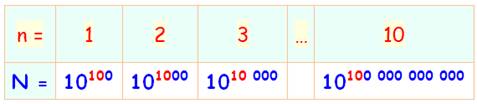
Maintenant que la mécanique du calcul est bien établie,
nous pouvons calculer Gogol à la
puissance Gogol (colonne de droite). Un 1 suivi de 10102 zéros. Note: 100 x 10100 = 102 x 10100
= 102 + 100 = 10102 |
|
|
|
||
|
Exemple de lecture |
|
|
|
Voir Calculs / Plus grand nombre avec trois
chiffres Voir site: A054382 |
||
|
|
|
|
Exemple
|
|
Voir Application
|
|
||
|
Abbreviated
as 9 to the 9 to the 9 |
|
|
|
|
|
|
Curiosité
|
|
Voir Racines
à étages
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()