NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/08/2021 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Algèbre
Débutants Algèbre	IDENTITÉS			Glossaire Algèbre
INDEX Identités	Remarquables	Degré > 2	Trigonométrie	Euler & Riemann
	Binôme	Spéciales	Puissance 5	x^n – 1
	(x+ x² + …) ^k	a^n – b^n	Inverses	Divers
		Sommaire de cette page >>> Approche >>> Formule >>> Explications >>> Autres triplets >>> Autres puissances

PUISSANCE 5 MAGIQUE!

Une curiosité avec 2 880 =>

Tous les multiples de 2 880 sont somme algébrique de huit puissances cinquièmes

Expliquée par 5² – 4² – 3² = 0 5^4 – 4^4 – 3^4 = 288

Voici l'explication et la généralisation.

Encore un effet des triplets de Pythagore.

Approche
Sommes algébriques de huit puissances 5 et expression avec triplet de Pythagore, sauf que les nombres sont mis à la puissance 4.	2 880 = 1^5 + 1^5 + 2^5 + 3^5 – 4^5 – 4^5 – 5^5 + 6^5 = 10 (5^4 – 4^4 – 3^4) = 10 x 288 5 760 = 2 x 2 880 = 1^5 + 2^5 + 2^5 + 2^5 – 3^5 – 5^5 – 6^5 + 7^5 = 20 (5^4 – 4^4 – 3^4) = 20 x 288 8 640 = 3 x 2 880 = 0^5 + 1^5 – 2^5 + 3^5 + 3^5 – 6^5 – 7^5 + 8^5 = 30 (5^4 – 4^4 – 3^4) = 30 x 288 28 880 = 10 x 2 880 = 5^5 – 6^5 – 7^5 + 10^5 + 10^5 – 13^5 – 14^5 + 15^5 = 100 (5^4 – 4^4 – 3^4) = 100 x 288

Formule
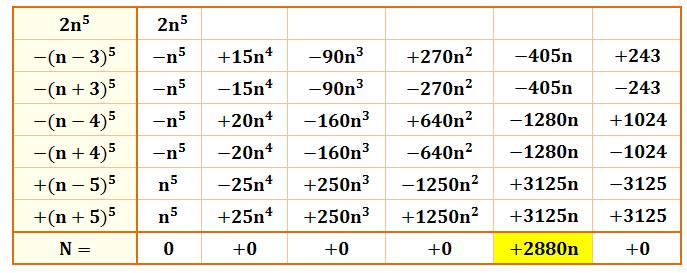
N = n^5 – (n – 3)^5 – (n – 4)^5 + (n – 5)^5 + n^5 – (n + 3)^5 – (n + 4)^5 + (n + 5)^5 N est divisible par 2 880
Rappel (a – b)^5 = a^5 – 5 a^4b + 10 a^3b^2 – 10 a^2b^3 + 5 ab^4 – b^5 Voir Développement de la puissance 5 Calcul Triplet de Pythagore En colonne 3 du développement qui correspond à 5ab^4: 5 n (– 9 – 9 – 16 – 16 + 25 + 25) = 10 n (– 3² – 4² + 5²) = 2 880 n Remarquable du fait que (3, 4, 5) forment un triplet de Pythagore. Tout autre triplet induirait la même propriété. >>>
Exemple de calcul avec n = 1 N = n^5 – (n – 3)^5 – (n – 4)^5 + (n – 5)^5 + n^5 – (n + 3)^5 – (n + 4)^5 + (n + 5)^5 N = 1^5 – (1 – 3)^5 – (1 – 4)^5 + (1 – 5)^5 + 1^5 – (1 + 3)^5 – (1 + 4)^5 + (1 + 5)^5 N = 1^5 – (– 2)^5 – (– 3)^5 + (– 4)^5 + 1^5 – (4)^5 – (5)^5 + (6)^5 N = 1^5 + 2^5 + 3^5 – 4^5 + 1^5 – 4^5 – 5^5 + 6^5 N = 1+ 32 + 243 – 1 024 + 1 – 1 024 – 3 125 + 7 776 N = 8 053 – 5 173 = 2 880

Autres triplets – Exemples
Triplet (5, 12, 13)	N = n^5 – (n – 5)^5 – (n – 12)^5 + (n – 13)^5 + n^5 – (n + 5)^5 – (n + 12)^5 + (n + 13)^5 N est divisible par 72 000 72 000 = 1^5 + 1^5 + 4^5 – 6^5 + 11^5 – 12^5 – 13^5 + 14^5 = 10 (13^4 – 12^4 – 5^4) = 10 x 7 200 144 000 = 2 x 72 000 = 2^5 + 2^5 + 3^5 – 7^5 + 10^5 – 11^5 – 14^5 + 15^5 = 20 (13^4 – 12^4 – 5^4) = 20 x 7 200
Triplet (7, 24, 25)	N = n^5 – (n – 7)^5 – (n – 24)^5 + (n – 25)^5 + n^5 – (n + 7)^5 – (n + 24)^5 + (n + 25)^5 N est divisible par 564 480 564 480 = 1^5 + 1^5 + 6^5 – 8^5 + 23^5 – 24^5 – 25^5 + 26^5 = 10 (25^4 – 24^4 – 7^4) = 10 x 56 448 11 228 960 = 2 x 564 480 = 2^5 + 2^5 + 5^5 – 9^5 + 22^5 – 23^5 – 26^5 + 27^5 = 20 (25^4 – 24^4 – 7^4) = 20 x 56 448

Autres puissances
Puissance 2	N = n^2 – (n – 5)^2 – (n – 12)^2 + (n – 13)^2 + n^2 – (n + 5)^2 – (n + 12)^2 + (n + 13)^2	= 0
Puissance 3	N = n^3 – (n – 5)^3 – (n – 12)^3 + (n – 13)^3 + n^3 – (n + 5)^3 – (n + 12)^3 + (n + 13)^3	= 0
Puissance 4	N = n^4 – (n – 5)^4 – (n – 12)^4 + (n – 13)^4 + n^4 – (n + 5)^4 – (n + 12)^4 + (n + 13)^4	= 576
Puissance 5	N = n^5 – (n – 3)^5 – (n – 4)^5 + (n – 5)^5 + n^5 – (n + 3)^5 – (n + 4)^5 + (n + 5)^5	2 880 n
Puissance 6	N = n^6 – (n – 3)^6 – (n – 4)^6 + (n – 5)^6 + n^6 – (n + 3)^6 – (n + 4)^6 + (n + 5)^6	8 640 n² + 21 600

Suite	Identités pour degré supérieur à 2 Identités en x + x² + x^3 + … à une puissance Formule du binôme Somme des entiers, des carrés, des inverses… Identité de Brahmagupta Identités fractions Identités trigonométriques Identités nombres complexes Identités entre puissances Utilisation pour calcul de puissances complexes
Voir	Carré des nombres en aaa…ab Constantes Différences entre puissances Isopérimètre Magie – Index Pépites Somme de carrés de nombres consécutifs Somme des entiers, des carrés… Somme et produit – Trouver les deux nombres Tautochronie Théorèmes
DicoNombre	Nombre 288 Nombre 2 880
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Identite/IdentP5.htm