![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page For
this page, refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
MULTIPLICATIONS des nombres à deux et trois chiffres & Généralisation On va examiner les méthodes
utilisées par ceux qui calculent rapidement notamment les Indiens
(védiques). Le
calcul est optimisé selon les nombres à multiplier. On
utilise les identités
remarquables. Voir
tout de suite de truc pratique pour la multiplication rapide >>> |
Trucs de
calcul rapide pour multiplications particulières
|
|
|
|
|
|
|
|
||||
|
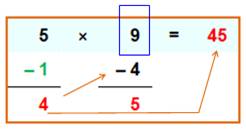
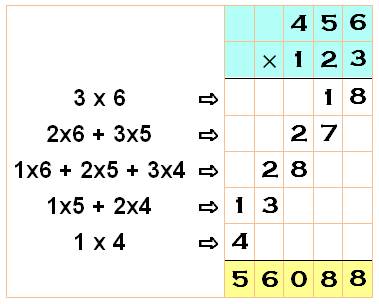
Méthode basée sur le même principe
avec le développement à trois chiffres
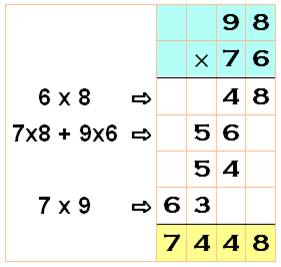
Voir Identités du premier degré Disposition pratique (mentale ou écrite) Produit
en colonne de droite / somme des produits en croix / produit en colonne de
gauche
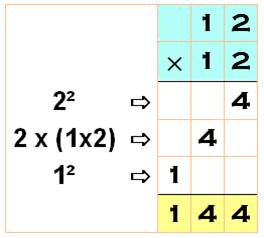
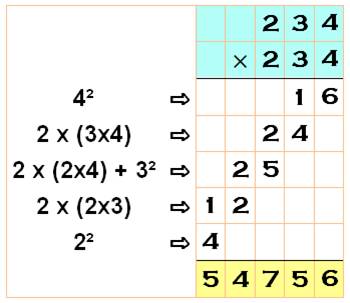
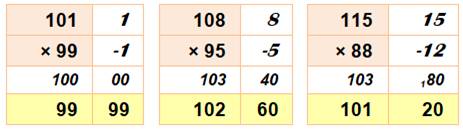
Cas des carrés (un peu de simplification)
|
||||
|
|
||||
|
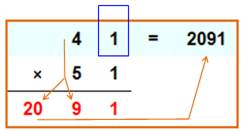
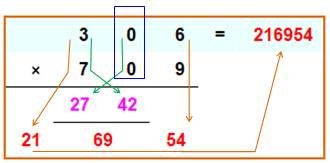
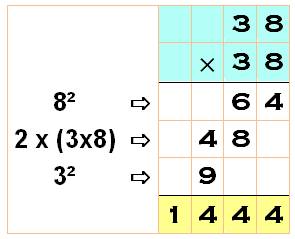
Méthode basée sur le même principe
avec le développement à trois chiffres
Voir Identités du premier degré Disposition
pratique (mentale ou écrite) avec aussi cas d'un carré
|
||||
|
|
|||
|
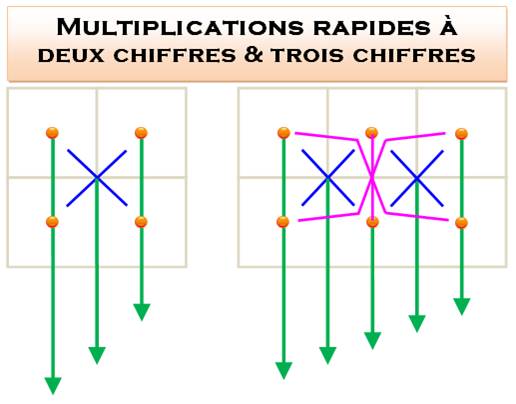
Principe |
Le principe a été vu sur deux exemples (2 et 3 chiffres). Voici la généralisation et la méthode pratique de calcul. |
||
|
Deux règles |
|
||
|
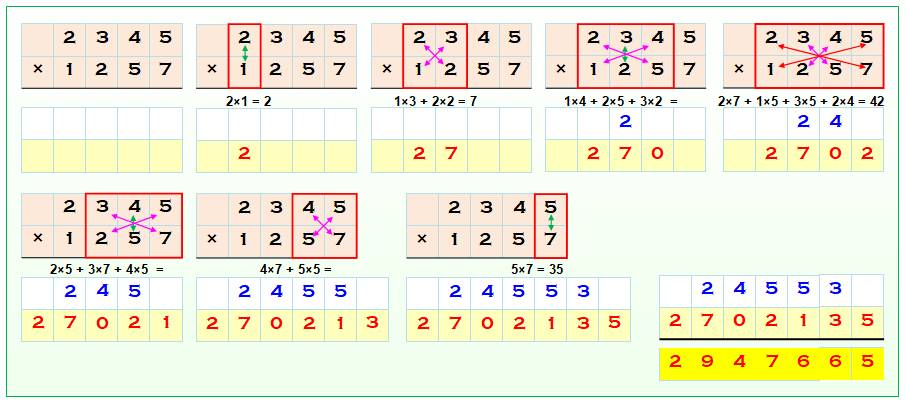
Exemple détaillé
|
|||
|
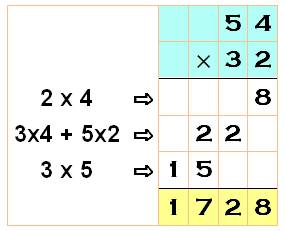
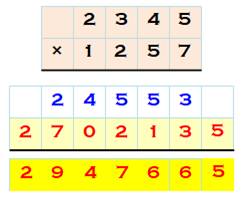
Disposition pratique avec
l'habitude |
On calcule de gauche à droite en
posant les résultats de calcul mental sur deux lignes, les dizaines en haut
et les unités en bas, en décalant d'un cran évidemment. Ne reste plus qu'à faire l'adition finale. |
|
|
![]()
|
|
|||
|
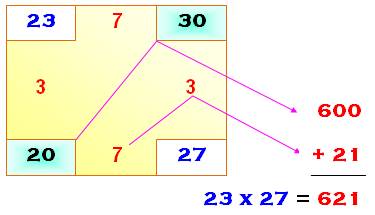
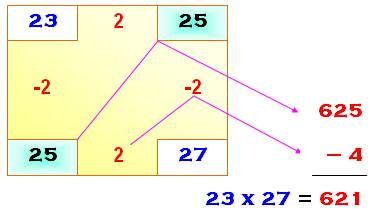
Disposition classique Méthode
élégante basée sur l'identité: Toute
l'astuce consiste à choisir le pivot c,
tel que le produit (a
+ c) (b – c) soit facile à calculer. Dans le premier exemple avec 23 x
27, on calcule graphiquement cette opération: Dans le deuxième exemple, on montre
qu'il est possible de choisir un pivot créant des écarts négatifs. |
|
||
|
Autre disposition De la multiplication désirée à
gauche, on passe à la multiplication simplifiée à droite. On corrige le résultat par le
produit interne indiqué (rouge par bleu). |
|
||
|
|
|||
|
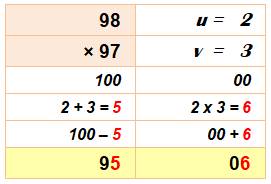
Procédé (cas des nombres inférieurs
à 100)
|
Exemple complet
|
||
|
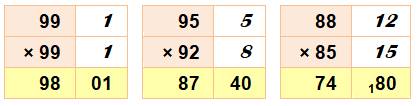
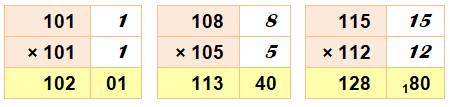
Deux
nombres inférieurs à 100: Méthode
basée sur l'identité: 10000 – 100(x + y) + xy Deux
nombres dépassant 100: 10000 + 100(x + y)
+ xy Deux
nombres autour de 100: 10000 + 100(x – y) – xy |
Exemples pour calcul mental Simple / Typique / Limite
|
||
Voir Nombre 100
![]()
|
|
Général |
Mêmes Unités |
Mêmes dizaines |
Cas particuliers |
|
Général |
||||
|
Avec 1 |
|
|
|
|
|
5 |
|
|
||
|
9 |
|
|
|
|
|
Autres |
|
|
|
Rappel
|
27 peut se décomposer en 20 + 7 ou 2 x 10 + 7 ou de manière générale Aa devient 10A + a |
On ne confondra pas dans cette page Aa qui indique deux nombres concaténées et A.a qui indique le produit
de A par a. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Cas particulier de la même
dizaine
Note: le dernier exemple montre que la
méthode vaut quel que soit le nombre de chiffres de A et B |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bilan
|
Selon le principe de ces pages, vous pouvez
compléter selon les unités ou les dizaines. Mais à multiplier les méthodes, on ne sait
plus laquelle utiliser. Pour deux et trois chiffres, il est souvent
plus judicieux de se référer à la méthode générale plutôt
que de chercher quel cas particulier à appliquer. |
![]()
|
Voir |
|
|
Livre |
|
|
Cette
page |
![]()