Ce site est désormais accessible en http://diconombre.fr/index.html et pour cette page voir le lien en fin de page For this page, refer to the link at the bottom.

22 Novembre 2025

NOMBRES - Curiosités, théorie et usages

Accueil DicoNombre Rubriques Nouveautés Édition du: 08/04/2026

Orientation générale  DicoMot Math Atlas Actualités M'écrire

Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths

DIVISION

Débutants

Division

Divisibilité

Glossaire

Division

Index général

>>> INDEX

Index Divisibilité

A^n + B^n

Somme puissances

A² + B²

A^n – B^n

Soustraction puissances

Sommaire de cette page

>>> identités remarquables en aⁿ – 1ⁿ

>>> Identités remarquables en aⁿ – bⁿ

>>> Programmation

>>> Divisibilité de aⁿ – bⁿ par (a – b) et (a + b)

>>> Applications numériques – Cas d'une puissance diminuée d'une unité

>>> Autres exemples

Divisibilité de Aⁿ – Bⁿ

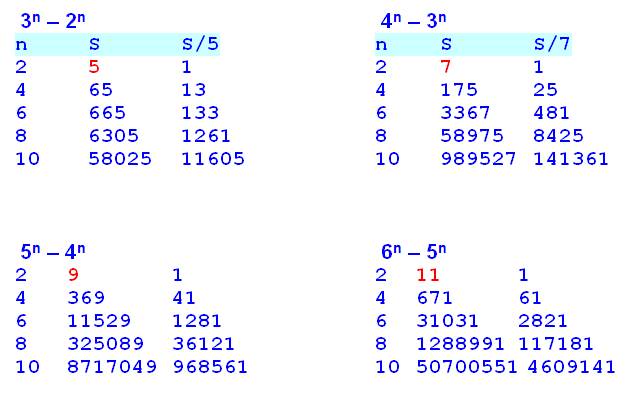
aⁿ – bⁿ est toujours divisible par (a – b)

Ex: 7ⁿ – 3ⁿ divisible par 7 – 3 = 4

7ⁿ – 6ⁿ divisible par 7 – 6 = 1, et par 13 si n est pair.

Cas où b = 1; où il est question de repdigits

Le développement montre qu'un nombre à une puissance auquel on soustrait un, est un nombre composé; et, il s'écrit comme un repdigit dans la base puissance moins un. C'est un nombre brésilien.

Voir Identités remarquables

Identité en aⁿ – 1ⁿ

Voir Nombres brésiliens / Sommes des puissances successives d'un nombre

Application aux puissances de 2

Voir Puissance de 2

Identités remarquables en a^n – b^n

Développement de a^n – b^n selon la valeur de n, avec mise en évidence des facteurs en (a + b et (a – b) Exemple de lecture pour n = 4 => a^4 – b^4 = (a – b) (a + b) (a²+ b²). Propriété (a – b) est toujours un facteur de a^n – b^n, et (a + b) est aussi un facteur pour n pair. (a² + b²) pour n divisible par 4. (a² + ab + b²) pour n divisible par 3. Et d'autres à découvrir … Notez les formes factorisées pour les puissances de 2, comme: Pas de magie! Applications en cascade d'une identité remarquable classique: a^32 – b^32 = (a^16 – b^16) (a^16 + b^16) = (a^8 – b^8) (a^8 + b^8) (a^16 + b^16) = …

Table des identités pour n de 2 à 20

Merci à Benoit P. pour son aide

Programmation Maple
Programme Alternative abrégée	Programme très simple avec mise en place d'une boucle qui explore les valeurs de n de 2 à 4. La mémoire A prend la valeur littérale a^n – b^ndont la factorisation est placée dans la mémoire B. Impression de ce que contiennent A et B avec le signe égal placé entre les deux. L'alternative en une seule instruction est possible sans risque d'erreur ici, bien que déconseillée pour des programmes un peu plus complexes.

Voir Programmation – Index

Divisibilité de a^n – b^n par (a – b) et (a + b)
Puissance n = 2k (paire) Divisible par a – b Divisible par a + b	a – b a + b	| a^n – b^n avec n = 2k | a^n – b^n avec n = 2k
Puissance n = 2k+1 (impaire) Divisible par a – b	a – b	| a^n – b^n avec n = 2k+1
Conclusion a^n – b^n est divisible par a – b pour toutes les puissances n impaires. et en plus par a + b pour les puissances n paires.

Applications numériques Cas d'une puissance diminuée d'une unité
Exemple 3^4 – 1^4 = 81 – 1 = 80 = 2 x 40 (divisible par 3 – 1 = 2) = 8 x 10 (divisible, en plus par 3 + 1 = 4) Généralisation Toutes les puissances, paires et impaires, de a, diminuées d'une unité, sont divisibles par a -1 Toutes les puissances paires de a, diminuées d'une unité, sont divisibles par a² -1

Autres exemples (divisibilité pour les puissances paires)
Exemple 5^4 – 4^4 = 625 – 256 = 369 qui est divisible par (5 + 4) = 9, en effet: 369 = 9 x 41

Suite	Applications numériques
Voir	Divisibilité – Index Somme de puissances Diviseurs Nombres consécutifs Formes polynomiales divisibles
Cette page	http://diconombre.fr/Wwwgvmm/Decompos/Divanmbn.htm