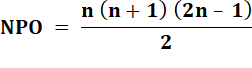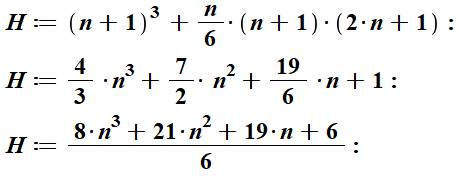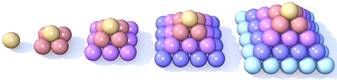
Almanach des nombres - nombre pyramide

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 28/03/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres
Débutants Nombres géométriques	Type Géométrique			Glossaire Nombres géométriques
INDEX Nombres Géométriques	Pairs / Impairs	Carrés	Cubes	Centrés
	Proniques	Pentagonal et suite	Tétraédriques	Hex
	Triangulaires	Grappes	Pyramidaux
		Sommaire de cette page >>> Listes des nombres pyramidaux >>> Nombres pyramidaux >>> Propriétés des pyramidaux carrés >>> Nombres octaédriques >>> Nombres pyramide octogonale

NOMBRES PYRAMIDAUX

Nombres figurés associés à la pyramide

à base triangulaire => Nombres tétraédriques (Illustration)

à base carrée => Nombres pyramidaux carrés

Correspond à l'empilement de boulets en couches sur une base triangulaire ou carrée (cannonball problem).

Anglais: Tetrahedral numbers and square pyramid numbers

Listes des nombres pyramidaux selon la figure de base

En rouge, les nombres présents plusieurs fois

Triangle ou Tétraédriques	1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969, 1140, 1330, 1540, 1771, 2024, 2300, 2600, 2925, 3276, 3654, 4060, 4495, 4960, 5456, 5984, 6545, 7140, 7770, 8436, 9139, 9880, 10660, 11480, 12341, 13244, 14190, 15180...		A000292
Carré	1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109, 2470, 2870, 3311, 3795, 4324, 4900, 5525, 6201, 6930, 7714, 8555, 9455, 10416, 11440, 12529, 13685, 14910, 16206, 17575, 19019, 20540, 22140, 23821, 25585, 27434, 29370... 1 5 14 30 55 Source image: The square pyramid numbers –Next number & Quora – Nick Shales	P(n) = 1² + 2² +…+ n² P(n) = P(n – 1) + n²	A000330
Pentagone	1, 6, 18, 40, 75, 126, 196, 288, 405, 550, 726, 936, 1183, 1470, 1800, 2176, 2601, 3078, 3610, 4200, 4851, 5566, 6348, 7200, 8125, 9126, 10206, 11368, 12615, 13950, 15376, 16896, 18513, 20230, 22050, 23976, 26011, 28158, 30420, 32800, 35301, 37926, 40678 …		A002411
Hexagonal	1, 7, 22, 50, 95, 161, 252, 372, 525, 715, 946, 1222, 1547, 1925, 2360, 2856, 3417, 4047, 4750, 5530, 6391, 7337, 8372, 9500, 10725, 12051, 13482, 15022, 16675, 18445, 20336, 22352, 24497, 26775, 29190, 31746, 34447, 37297, 40300 …		A002412
Heptagonal	1, 8, 26, 60, 115, 196, 308, 456, 645, 880, 1166, 1508, 1911, 2380, 2920, 3536, 4233, 5016, 5890, 6860, 7931, 9108, 10396, 11800, 13325, 14976, 16758, 18676, 20735, 22940, 25296, 27808, 30481, 33320, 36330, 39516, 42883, 46436, 50180, 54120 ...		A002413
Octogonal	1, 9, 30, 70, 135, 231, 364, 540, 765, 1045, 1386, 1794, 2275, 2835, 3480, 4216, 5049, 5985, 7030, 8190, 9471, 10879, 12420, 14100, 15925, 17901, 20034, 22330, 24795, 27435, 30256, 33264, 36465, 39865, 43470, 47286, 51319, 55575, 60060, 64780, …		A002414

Voir Autres pyramidaux

119 nombres pyramidaux

de 0 à 5000

jusqu'à octogonaux

1, 4, 5, 6, 7, 8, 9, 10, 14, 18, 20, 22, 26, 30, 35, 40, 50, 55, 56, 60, 70, 75, 84, 91, 95, 115, 120, 126, 135, 140, 161, 165, 196, 204, 220, 231, 252, 285, 286, 288, 308, 364, 372, 385, 405, 455, 456, 506, 525, 540, 550, 560, 645, 650, 680, 715, 726, 765, 816, 819, 880, 936, 946, 969, 1015, 1045, 1140, 1166, 1183, 1222, 1240, 1330, 1386, 1470, 1496, 1508, 1540, 1547, 1771, 1785, 1794, 1800, 1911, 1925, 2024, 2109, 2176, 2275, 2300, 2360, 2380, 2470, 2600, 2601, 2835, 2856, 2870, 2920, 2925, 3078, 3276, 3311, 3417, 3480, 3536, 3610, 3654, 3795, 4047, 4060, 4200, 4216, 4233, 4324, 4495, 4750, 4851, 4900, 4960.

NOMBRES PYRAMIDAUX

Tétraédrique (les 100 plus petits) ou pyramidal triangle

1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969, 1140, 1330, 1540, 1771, 2024, 2300, 2600, 2925, 3276, 3654, 4060, 4495, 4960, 5456, 5984, 6545, 7140, 7770, 8436, 9139, 9880, 10660, 11480, 12341, 13244, 14190, 15180, 16215, 17296, 18424, 19600, 20825, 22100, 23426, 24804, 26235, 27720, 29260, 30856, 32509, 34220, 35990, 37820, 39711, 41664, 43680, 45760, 47905, 50116, 52394, 54740, 57155, 59640, 62196, 64824, 67525, 70300, 73150, 76076, 79079, 82160, 85320, 88560, 91881, 95284, 98770, 102340, 105995, 109736, 113564, 117480, 121485, 125580, 129766, 134044, 138415, 142880, 147440, 152096, 156849, 161700, 166650, 171700

Pyramidaux carrés (les 100 plus petits)

1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109, 2470, 2870, 3311, 3795, 4324, 4900, 5525, 6201, 6930, 7714, 8555, 9455, 10416, 11440, 12529, 13685, 14910, 16206, 17575, 19019, 20540, 22140, 23821, 25585, 27434, 29370, 31395, 33511, 35720, 38024, 40425, 42925, 45526, 48230, 51039, 53955, 56980, 60116, 63365, 66729, 70210, 73810, 77531, 81375, 85344, 89440, 93665, 98021, 102510, 107134, 111895, 116795, 121836, 127020, 132349, 137825, 143450, 149226, 155155, 161239, 167480, 173880, 180441, 187165, 194054, 201110, 208335, 215731, 223300, 231044, 238965, 247065, 255346, 263810, 272459, 281295, 290320, 299536, 308945, 318549, 328350, 338350

Pyramidaux carrés de dimension 4

= somme cumulée des pyramidaux de dimension 3

1, 6, 20, 50, 105, 196, 336, 540, 825, 1210, 1716, 2366, 3185, 4200, 5440, 6936, 8721, 10830, 13300, …

Voir Quantité de carrés dans une grille carrée

Construction

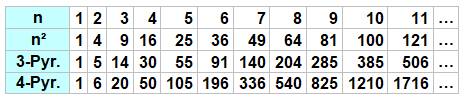
3-pyramidaux = somme cumulée des carrés.

4-pyramidaux = somme cumulée des 3-pyramidaux.

24^ème pyramidal

Le seul nombre pyramidal carré à être un nombre carré.

Autres carrés, somme de 24 carrés consécutifs:

11 236 = 106² = 9² + 10² + … + 32²

24 964 = 158² = 20² + 21² + … + 43²

33 124 = 182² = 25² + 26² + … + 48²

75 076 = 274² = 44² + 45² + … + 67²

184 900 = 430² = 76² + 77² + … + 99²

Etc.

Voir Sommes de carrés consécutifs – Problème de Lucas

PROPRIÉTÉS des PYRAMIDAUX CARRÉS

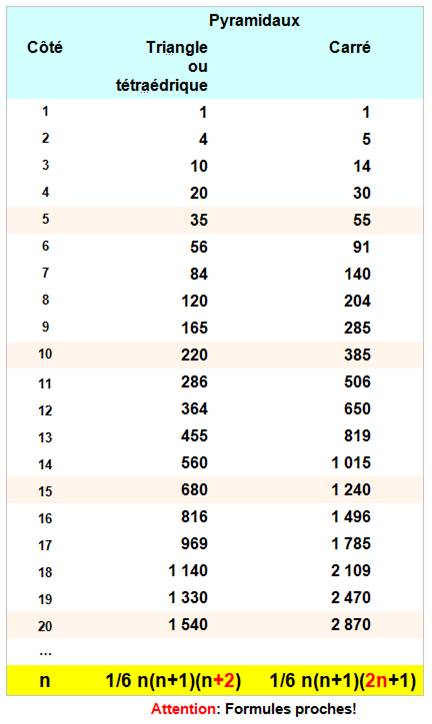
Formule de calcul

Pycar_n = n (n + 1) (2n + 1) / 6

Pycar_n = 1² + 2² + 3² + … + n² >>>

Pycar_n = Pycar_n-1 + n²

Conséquences

Un parallélépipède de longueur 2n+1, de largeur n+1 et de profondeur n contient 6 pyramides carrées.

Un nombre pyramidal carré étant un nombre entier,

Tout produit de trois nombres de cette sorte est divisible par 6.

Somme des carrés

Un nombre pyramidal carré est égal au cumul des nombres carrés:

30 = 1 + 4 + 9 + 16.

Chacun est égal à son prédécesseur plus le carré correspondant

30 = 14 + 16.

Carrés	Pyramidaux
1	1
4	5
9	14
16	30
Nombre de billes qu'il faut ajouter à une pyramide pour ajouter une rangée à la base de la pyramide.	Cumul: nombre de billes dans la pyramide à base carrée. Ou, SOMME des carrés successifs.

Voir Somme des carrés des nombres consécutifs

Relations

avec tétraédriques

Pycar_n

= 1/6 n (n + 1) (2n + 1)

= Tet_n-1 + Tet_n

= 1/6 { (n-1)n(n+1) + n(n+1)(n+2) }

= 1/6 n(n+1) { (n-1) + (n+2) }

= 1/6 n(n+1) { 2n+1 }

= 1/ 3 T_n x (2n+1)

= 1/3 x 1/2 n(n+1) (2n+1)

Pycar₄

= 4 x 5 x 9 / 6 = 30

= 10 + 20

= 10/3 x (2x4+1)

= 30

Nombres OCTAÈDRIQUES
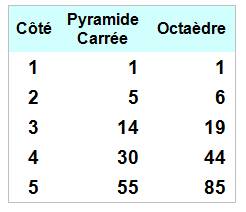
Définition	Il s'agit de deux pyramides à base carrée empilées l'une sur l'autre par leur base.
Formule de calcul	Octa_n = Pyra_n-1 + Pyra_n = 1/3 n (2n² + 1)
Relation	Octa_n – Octa_n-1 = Cube centré
Liste	1, 6, 19, 44, 85, 146, 231, 344, 489, 670, 891, 1156, 1469, 1834, 2255, 2736, 3281, 3894, 4579, 5340, 6181, 7106, 8119, 9224, 10425, 11726, 13131, 14644, 16269, 18010, 19871, 21856, 23969, 26214, 28595, 31116, 33781, 36594, 39559, 42680, 45961, 49406, 53019, 56804, 60765, 64906, 69231, 73744, 78449, 83350, 88451, 93756, 99269, 104994, …

Nombres pyramide octogonale
Définition	Empilement en pyramide sur base octogonale.
Formule de calcul
Liste	1, 9, 30, 70, 135, 231, 364, 540, 765, 1045, 1386, 1794, 2275, 2835, 3480, 4216, 5049, 5985, 7030, 8190, 9471, 10879, 12420, 14100, 15925, 17901, 20034, 22330, 24795, 27435, 30256, 33264, 36465, 39865, 43470, 47286, 51319, 55575, 60060, 64780, 69741, 74949, 80410, 86130, 92115, 98371, 104904, …
Programme Maple

Voir Programmation – Index

Nombres Maisons
Définition	Cube surmonté d'une pyramide (à base carrée).
Formules de calcul
Exemple n = 3	H(3) = 4³ + (3 x 4 x 7) / 6 = 64 + 14 = 78
Liste des 100 plus petits	1, 9, 32, 78, 155, 271, 434, 652, 933, 1285, 1716, 2234, 2847, 3563, 4390, 5336, 6409, 7617, 8968, 10470, 12131, 13959, 15962, 18148, 20525, 23101, 25884, 28882, 32103, 35555, 39246, 43184, 47377, 51833, 56560, 61566, 66859, 72447, 78338, 84540, 91061, 97909, 105092, 112618, 120495, 128731, 137334, 146312, 155673, 165425, 175576, 186134, 197107, 208503, 220330, 232596, 245309, 258477, 272108, 286210, 300791, 315859, 331422, 347488, 364065, 381161, 398784, 416942, 435643, 454895, 474706, 495084, 516037, 537573, 559700, 582426, 605759, 629707, 654278, 679480, 705321, 731809, 758952, 786758, 815235, 844391, 874234, 904772, 936013, 967965, 1000636, 1034034, 1068167, 1103043, 1138670, 1175056, 1212209, 1250137, 1288848, 1328350, 1368651

Anglais: House numbers

Suite	Pair et impairs Voir haut de page Pyramide (polyèdre) Pyramide des âges Kheops
Nombres géométriques	Introduction Valeurs Théorie
Aussi	Liste des noms des nombres Nombres pyramides (ou en triangle) Partition Somme de carrés consécutifs = carré Géométrie – Index
Site	Sum of Consecutive Nth Powers Equals an Nth Power – MathPages OEIS A002414 – Octagonal pyramidal numbers: a(n) = n(n+1)(2*n-1)/2 OEIS A051662 - House numbers: a(n) = (n+1)^3 + Sum_{i=1..n} i^2 House numbers – Numbers Aplenty
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/CinqNbPy.htm