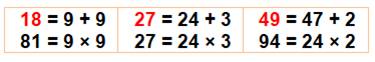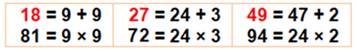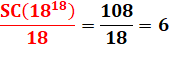Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 05/05/2025 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	10	11		12	13		14	15	16	17	18	19

Nombre 18	Culture 18	Maths 18	Sciences 18
	Culture 18

Dix-huit

Eighteen

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1 0010
Bases	2003 335 228
Romain	XVIII

Suite

Préfixes diviseurs et multiplicateurs:

10^-18 atto

10 ¹⁸ exa (trillion)

(É-U: quintillion)

Remarquable

Caractérisation du nombre

2-rond

ABA (2 . 3²)

Abondant

Abondant (hautement -)

Abondant primitif

Complémenté

Composé

Coster

Curzon

Dihédral

Dissécable

Friable (2٠3²)

Harshad

Hofstadter – NON

Idonéal

Interpremier (17, 18, 19)

Lucas

Narcissique de Keith

Narcissique généralisé

Pair

Pratique (panarithmétique)

Prodigue

Queneau

Ramsey (4,4) et (3,6)

Refactorisable ou tau

Semi-parfait

Totient faiblement

Ulam

Heptagonal (3^e)

Pyramide pentagonale (3^e)

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Rappel Propriétés générales >>>

Numération – Chiffres

	De nombreux multiples de 18 s'écrivent avec cinq chiffres romains. Voir Nombre 36
18 + 81 = 99	Devient palindrome en lui ajoutant son retourné.
18 = 2 x (1 + 8) 81 = 9 x (8 + 1)	Seul nombre dont la somme des chiffres est son double. 27 l'est pour le triple. Son retourné est neuf fois la somme d ses chiffres.
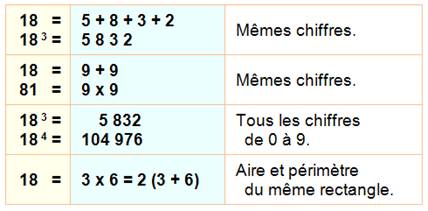
18 = 1 + 8 + 3 + 2 + 4	Narcissique de Keith. Somme de ses chiffres et de ceux de son carré.
18 [20, 10, 52] Cycle: 18, 9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1	Le cycle de Syracuse de 18 comporte 20 étapes, un record. Il atteint une altitude maximale avec 52 au rang 10.
		Motifs avec sommes et produits. Les trois seuls cas à deux chiffres. Voir Nombre 497

Addition – Partition

p(18) = 385	Quantité de partitions du nombre.
18 = 1 + 6 + 11	3^e Nombre heptagonal.
18 = 3 + 4 + 5 + 6 = 5 + 6 + 7	Deux seules sommes de nombres consécutifs >>>
ProdCh(36) = 3 x 6 = 18 SomCh(36²) = SomCh(1296) = 18	Égalité avec opérations sur les chiffres.
18 / (1 + 8) = 2	Nombre de Moran car, divisé par la somme de ses chiffres, le quotient est un nombre premier.
18 = 1 + 9 + 8	Amusement avec disparition du 9.
18 = 3 + 7 + 8 = 4 + 5 + 9 122 = 3² + 7² + 8² = 4² + 5² + 9² 18 = 2 + 7 + 9 = 3 + 5 + 10 134 = 2² + 7² + 9² = 3² + 5² + 10² 18 = 1 + 8 + 9 = 3 + 4 + 11 146 = 1² + 8² + 9² = 3² + 4² + 11² 18 = 1 + 7 + 10 = 2 + 5 + 11 150 = 1² + 7² + 10² = 2² + 5² + 11² 18 = 1 + 4 + 6 + 7 = 2 + 3 + 5 + 8 102 = 1² + 4² + 6² + 7² = 2² + 3² + 5² + 8²		Cinq égalités valables pour les entiers comme pour leur carré. Plus petit nombre avec ce record.
18 = 1 + 7 + 2 + 8 = 1 + 7 + 4 + 6 = 1 + 8 + 3 + 6 = …	Cubes magiques de somme 18.
18 = 6 + 5 + 4 + 3 = 2 x 9	Somme de consécutifs, égale à un multiple du précédent. Elle vaut deux fois la somme des symétriques.
18 = 4! – 3! = 24 – 6 = 3² x 2! = 3! x 3	Différence de factorielles: toujours du type: (n+1)! – n! = n · n! = n² ·(n-1)!
18, 11124 & 111222 1+8 = 1+1+1+2+4 = 1+1+1+2+2+2 & 1x8= 1x1x1x2x4 = 1x1x1x2x2x2	Même somme des chiffres et même produit.

Devinette

Quelles sont les dimensions du rectangle qui a le même nombre pour l'aire et le périmètre (l'un en m² et l'autre en m)?

Périmètre = 2a + 2b = a.b = Aire

Seule solution a = 3 et b = 6

Voir Explications

Multiplication et division

18 = 2.3²	Le 10^e nombre composé.
18 = 3 x 6 = 2 (3 + 6)	Produit / somme = 2 (Voir devinette ci-dessus)
Somme des diviseurs propres = 21	Le plus petit nombre abondant terminé par 8.
18 est pratique ou panarithmétique (tous les nombres jusqu'à 18 sont sommes de certains de ces diviseurs)	Ses diviseurs sont 1, 2, 3, 6, 9, 18. Et : 1 = 1; 2 = 2; 3 = 3; 4 = 1 + 3; 5 = 2 + 3; 6 = 6; 7 = 1 + 6; 8 = 6 + 2; 9 = 9; 10 = 9 + 1; 11 = 9 + 2; 12 = 9 + 3; 13 = 9 + 3 + 1; 14 = 9 + 3 + 2; 15 = 9 + 6; 18 = 18.
18 = tau (180)	Quantité de diviseurs de 180.
	Un des sept nombres ayant cette propriété: la quantité de diviseurs est égale à la quantité de nombres premiers avec lui et inférieurs à lui (totient).
18	Plus petit cas où la quantité de diviseurs atteint 18. Précédent 120 avec 16 diviseurs; suivant 240 avec 20.
13, [18, 152, 3 024] 18 = 2x3² et 19 = 19 => 19 – 6 = 13	Plus petit nombre tel que son radical est égal au radical du suivant moins k.
D(18) = 1, 2, 3, 6, 9, 18	Nombre à facteurs parfaits. La somme des quantités de diviseurs de ces chiffres est égale à 18.
Facteurs de 18 = {2, 3} + 2 => {4, 5} qui divisent 18 + 2 = 20	Nombre facteur-3-diviseur. Le plus petit tel nombre.
PGCD(18, 2k+1 < 18) = 1	Les 5 nombres impairs premiers avec 18 (5, 7, 11, 13, 17) sont effectivement premiers.
18, 18, 36, 18	Les nombres premiers mod 90 présentent une propriété octodédimale.

18 = (1 + 8) x 2	Seul nombre deux fois la somme de ses chiffres. Cf. Résolution de 10a + b = 2(a + b) => 8a = b dont la seule solution est a = 1 et b = 8.
18 = 7 + 11	Somme de premiers consécutifs.
	Mêmes chiffres de part et d'autre de l'égalité.
18 = (3 x 21) – (3 x 15) = 63 – 45	Solution de l'équation: 3(x + 3) - 3(x - 3) = x
18 = (4+2) + (4–2) + (4x2) + (4/2)	Somme des quatre opérations.
18 = 2 . 3^2	Nombre en puissance de 2 et 3.
18 = 9 x 2 = (10–1 ) (10–8) = 9 x 2	Nombre complémenté. Les suivants sont 35 et 315 En éliminant 50, 500, etc. qui sont terminés par des zéros.
18 = 1/4 x 2x3 x 3x 4	Quantité de rectangles dans un rectangle de 2 x 3.
18 = 9! / 20 160 18, 108, 1 008, 1 080, 10 080	Suite amusante de diviseurs de 9!

Puissances

18 = 3² + 3² = 1² + 2² + 2² + 3² = 1² + 1² + 4² = 1^3 + 1^3 + 2^3 + 2^3 = 1^4 + 1^4 + 2^4	Seules sommes de puissances de 2 à 5 avec deux à cinq termes.
18 = 2 x 3²	Nombre à motif a . b^a.
18 = 3^3 – 3^2 = 27 – 9	Différence de puissances d'un même nombre. Seul cas d'équation de Bachet pour k = 15. Différence entre un cube et un carré.
18 = 3^5 – 15^2 = 19^2 – 7^3	Différence entre puissances.
18 = 2^3 – 2x3^3 + 4^3 = 6 x 3	Expression avec 3 cubes, toujours multiple de 6.
	Différence entre racine carrée et racine cubique égal 18. Calcul proposé au calculateur prodige Giacomo Inaudi.
18 => {5, 7, 11, 13, 17}	Nombre dont les copremiers sont tous sans facteurs simples. Le dernier est 60.
18 = 7 + 2 + 9 & 729 = 9^3 = 1+7+2+8 & 1 728 = 12^3	Sommes des chiffres des cubes 18 est 36 fois une telle somme pour les nombres inférieurs à 1000.
18 = 3² + 3² = 1² + 1² + 4² 6 = 3 + 3 = 1 + 1 + 4	Égalité entre les nombres et entre leur carré.
	Nombre d'or et son inverse.

Nombre en puissance

= 4,242640…			Curiosité avec des chiffres pairs.
= 1,435188887884489…			Curiosité avec des 8.
18^2 = 324	La somme des chiffres du nombre et de son carré sont identiques (10). Liste: [1, 1], [9, 81], [18, 324], [19, 361], [45, 2025], [46, 2116], [55, 3025], [99, 9801]
18² = 324 = 2^2 x 3^4	Carré formé avec trois chiffres consécutifs.
18^3 = 5 832 & 5 + 8 + 3 + 2 = 18 18^6 = 34 012 224 & 3 + 4 + 0 +…2 + 4 = 18 18^7 = 612 220 032 & 6 + 1 + 2 +…3 + 2 = 18			Triple nombre NESCHIP.
18^3 = 5 832 18^4 = 104 976			Tous les chiffres à eux deux.
18^4 = 104 976			Plus petit bicarré à six chiffres différents.
18^4 = 104 976 & 1+0+4+9+7+6 = 27 27^4 = 531 441 & 5+3+1+4+4+1 = 18		Motif en couple.
	Un des trois nombres pannumériques puissants Tous les chiffres de 0 à 9, une seule fois.
18^5 = 18 89568	Nombre qui se retrouve en tête d'une de ses puissances.
	Somme des chiffres n^n divisible par n. Plus petit nombre à plus d'un chiffre avec cette propriété. Liste: 1, 2, 3, 9, 18, 27, 54, 90, 108, 163, 197, 254, 432, 1292, 2202, 9648, … OEIS A108827

Jeux

				Amusement avec leur retourné.
18 x 297 = 5 346 198 x 27 = 5 346			Chaque égalité utilise les neuf chiffres.
18 x 987 654 321 = 17 777 777 778 27 x 987 654 321 = 26 666 666 667 …			Produits avec les multiples de 9.
		Jeu du quatre 4.
18	Problème des 18 points. Il s'agit de choisir une suite de points sur un intervalle tel que les deux premiers soient dans des moitiés différentes de l'intervalle, les trois premiers soient dans des tiers différents, et ainsi de suite. Problème infaisable pour 18, mais réalisable pour 17.

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 0, 0, 1, 0] 3, [2, 0, 0] 4, [1, 0, 2] 5, [3, 3] 6, [3, 0]	7, [2, 4] 8, [2, 2] 9, [2, 0] 10, [1, 8] 11, [1, 7]	12, [1, 6] 13, [1, 5] 14, [1, 4] 15, [1, 3] 16, [1, 2]	5, [3, 3] 8, [2, 2] 17, [1, 1]

Voir Bases / Brésiliens

Suite	Voir le menu en haut de page Nombre 18 en culture générale Nombre 19
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres
Cette page	http://villemin.gerard.free.fr/NombDico/DixHuiNb.htm