![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page For
this page, refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Il y a trois sortes de personnes dans le
monde : ceux qui savent compter, et ceux qui ne
savent pas... |
Voir
Pensées & humour
|
NOMBRES face à l'ADDITION PARTITION Représentation des
nombres entiers par la somme d'entiers non nuls. On donne, ici,
diverses représentations des entiers par leurs sommes d'entiers, de premiers,
de carrés, de puissances. |
Orientation
|
pour
une nomenclature de tous les problèmes posés
par les sommes de puissances.
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Partition simple Notion
introduite par Euler. Les termes
sommés s'appellent les sommants ou parts
de la partition. Exemple: Il
y a 7 partitions de 5:
|
Diagramme de Ferrers Chaque
sommant est représenté par une quantité équivalente de points. Exemple avec 15
La
quantité de points (croix) est 15. 2 donne 2 points 5 donne 5 points etc. Voir Présentation
ci-dessous pour
le nombre 5 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Diagramme
de Ferrers: une manière originale de représenter les partitions
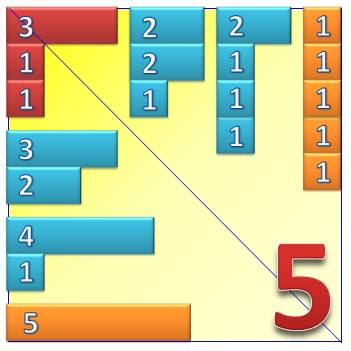
Voir Nombre 5
Merci à Riquier pour sa vigilance
|
|
|
|
Dénombrement La quantité de sommes pour
partitionner n est 2n-1 Exemple 3 = 1 + 1 + 1 = 1 +
2 = 2 + 1 : 4
possibilités (dont le nombre lui-même) = 23-1 = 4. Démonstration On
écrit tous les " 1 " dont la somme est n. On
forme toutes les possibilités des nombres à ajouter en mettant un espace
entre les blocs de " 1 " souhaités. et
un signe + entre les blocs ainsi constitués. Exemple 1 1 1 + 1 1 + 1
=> 3 + 2 + 1 On
dénombre les combinaisons de + entre ces blocs de " 1 ". |
|
Voir Développement sur les partitions
|
|
|
|
Théorème Tout nombre rationnel positif peut s'exprimer par une somme
finie de nombres différents de la suite harmonique
1/n. Propriété utilisée
Notez la suite des trois dénominateurs: a,
le nombre suivant et leur produit. Voir Cette propriété illustrée
avec le nombre 101. Exemples
Notez les nombres: a, somme, produit et b. Exemples
|
|
Voir Somme
donnant 0,5 / Somme des
inverses / Fractions
débutants / Fractions
/ Fractions égyptiennes
Belle relation à noter
|
Propriété de l'inverse
d'un nombre composé
Vérification
Exemple
Généralisation Cette
relation peut être étendue à plus de deux nombres. |
|
|
|
|
Somme des inverses et
unité Tout nombre supérieur
à 77 peut être décomposé en une somme d'entiers dont la somme des inverses est égale à l'unité. Exemple 78 = 2 + 6 + 8 + 10
+ 12 + 40
Théorème Pour tout entier n,
il existe a, b, c tel que :
Somme de nombres consécutifs Un entier est la
somme d'une suite d'entiers consécutifs si et
seulement si ce nombre n'est pas une puissance de deux. Somme de nombres abondants Tous les nombres
supérieurs à 20 161 sont la somme de 2
nombres abondants. |
|
|
|
||||||||||||||||||||||||||||||||||||
|
Carrés et impairs Théorème Les sommes des
nombres impairs forment des carrés. Exemples
Généralisation 1 + 3 + 5 + 7 + …
+ N = ((N+1) / 2)² Théorème La somme des N
premiers impairs est le carré de la moitié de ce nombre augmenté de un. Suite >>> Cubes et entiers La somme des cubes des nombres successifs est le carré de la somme de ces nombres. Suite >>> Cubes et nombres parfaits Tous les nombres parfaits sont la somme des cubes des nombres impairs consécutifs. 1 + 27 = 28 |
||||||||||||||||||||||||||||||||||||
Voir
Somme des entiers, pairs impairs
…
|
SOMME DE NOMBRES PREMIERS –
Goldbach
Tout entier pair > 2 est la somme de 2 premiers. Exemples 10
= 7+ 3 50
= 37+13 100 = 83 + 17 = 53 + 47 Tout entier impair > 7 est la somme de 3 premiers.
Autres théorèmes Tout nombre supérieur à 45 est décomposable en somme de nombres
premiers distincts supérieurs à 11. Tout nombre supérieur à 55 est décomposable en somme de nombres
premiers distincts de la forme 4n + 3. Tout nombre premier est un multiple
de 6 à ± 1 près. (Sauf 2 et 3). |
Voir Conjectures
|
SOMME DE NOMBRES
TRIANGULAIRES Théorème Tout nombre est
décomposable en somme d'au plus trois nombres triangulaires. Nombre = Généralisation de
Fermat Tout nombre est décomposable en somme de n nombres n-gulaires au plus: 3 nombres triangulaires, 4 nombres carrés, 5 nombres pentagonaux, 6 nombres hexagonaux ... |
Voir Nombres triangulaires / Théorème de Waring / Fermat
/ Nombres géométriques
Table de
sommes de triangulaires / Partition en nombres
triangulaires
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/Partiti1.htm
|
![]()
|
DIVISIBILITÉ
de CARRÉS par 4 et par 8
Pour
tous ces sujets voir >>> |


