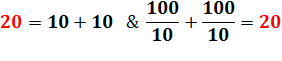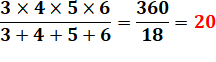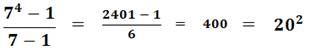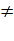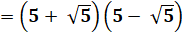|
Édition du: 13/07/2025 |
|
Dictionnaire des Nombres |
||||||||||||
|
100 / 200 |
||||||||||||
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||
|
Nombre abondant égal à la
somme de ses diviseurs abondants. Ils sont très nombreux. |
|||
|
Caractérisation
du nombre
|
|
Voir |
|
Rappel Propriétés générales >>>
|
Henri Frédéric
Amiel - 1866 Pour information:
1/20 x 3/70 = 1/466,6…arrondi
ici à 1/460. On sait que le
propre du génie est de fournir des idées aux crétins une vingtaine d'années plus tard. Louis
Aragon – Traité du style (1928) |
Voir
Pensées & humour
/ Nus en peinture
Nombre tétraédrique (tetrahedal number)
|
20 = 10 + 10 = 10
+ 6 + 4 = 10 + 6 + 3 + 1 =
somme des 4 premiers = (4
x 5 x 6) / 6 quatrième |
|
![]()
|
|
||
|
|
Chiffres et numération
|
20 =
vingt |
|
|
20
= (11 – 2) + (11 – 0) =
(4 – 2)² + (4 – 0)² |
|
|
xy + x + y ne donne
jamais 20 |
|
|
20 = 2 + 24 |
Somme de ses chiffres et de ceux de sa
puissance 4. |
|
202 = 400 (2 + 0)2 = 4 + 0 + 0 |
Liste: 0,
1, 2, 3, 10, 11, 12, 13, 20, 21, 22, 30, 31, 100, 101, … |
|
203 = 8000 (2 + 0)3 = 8 + 0 + 0 + 0 |
Liste: 0,
1, 2, 10, 11, 20, 100, 101, 110, 111, 200, 1000. |
|
20, 120,
200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 220, 320, 420, 520, 620,
720, 820, 920. |
k20 et 20k
sont composés; k = {0, 1,…, 9}. Liste: 20,
32, 62, 84, 114, 126, 134, 135, 146,
150,164, 168,176, 185, 192, 196, 204, … |
Addition et soustraction
|
p(20) = 627 |
|
||
|
20 =
2 + 3 + 4 + 5 + 6 |
|
||
|
= 2 + 4 + 5 + 9
= 2 + 3 + 7 + 8 |
|
||
|
20
= 2 + 4 + 6 + 8 = 2 + 3 + 4 + 5 + 6 |
|
||
|
20
= T1 + T2 + T3 + T4 |
|
||
|
20 =
10 + 10 et 10 x 10 = 100 |
|
||
|
20
= 1 + 4 + 5 + 10 |
|
||
|
20 = 1 + 7 + 12 = 3 + 4 + 13 194 = 1² + 7² + 12² = 3² + 4² + 13² 20 = 1 + 4 + 7 + 8 = 2 + 3 + 6 + 9 130 = 1² + 4² + 7² + 8² = 2² + 3² + 6² + 9² |
|
||
|
20
= 1x2 + 2x3 + 3x4 = 4x5 =
1²+2²+3² + 1+2+3 = 4² + 4 |
|
||
|
20
= (5+1) + (5–1) + (5x1) + (5/1) |
|||
|
|
|
||
Multiplication, division, diviseurs
|
20
= 4 x 5 |
|
|
|
20 =
(3 + 3)! / (3! x 3!) |
||
|
20 =
6 |
|
|
|
|
|
|
|
20
+ 11 = 31 20
+ 33 = 53 20
+ 77 = 97 |
Le plus petit cas avec
les repdigits pairs est 15 avec les repdigits 22, 44 et 66. Aucun avec les
quatre repdigits pairs. Voir Nombre 116
pour les nombres à deux chiffres |
|
|
|
|
|
|
20 => {3, 7, 9, 11, 13, 17, 19} |
|
|
|
20 = 2² x 5 21 = 3 x 7 22 = 2 x 11 |
|
|
|
tau' (20) = 22 |
|
|
|
20
=
tau (240) |
|
|
|
11,
[20, 27, 288, 675, 71 199] 20 = 2²x5 et 21 = 3x7 => 21 – 10 = 11 |
Partage
cette propriété avec les quatre nombres indiqués (n au moins jusqu'à 109). |
|
|
|
Liste: 20,
104, 464, 650, 1952, … |
|
|
|
Sigma prime est la somme des diviseurs stricts. |
|
|
|
Précédent
180 avec 18 diviseurs; suivant 360 avec 24. |
|
|
20 =
0² + 2² + 4² = 1² + 1² + 3² + 3² = 14 + 14 + 14
+ 14 + 24 |
|
|
20
= 6! / 3!² = 6! / 6² = 6! / (6 x 6) = 720 / 36 |
|
|
20
= 2² + 4² = (1² + 1²) (1² + 3²) = 3² + 3² + 1² + 1² |
|
|
20 =
63 – 14² = 216 – 196 |
Différence
entre un cube et un carré. |
|
20
= 42 + 22 = 41 + 42 = 6² – 4² = 52 – 51 = 63 – 142 |
|
|
20 = 2² + 4² |
|
|
20
= 12 + 12
+ 22 + 12 + 22 + 32 |
|
|
4,
10, 16, 20, 25, 26, 34, 36, 40, 50 … Voir Identité de Lagrange |
|
|
|
En puissance
|
202 =
52² – 48² = (50+2)² – (50–2)² |
|
||||||||||
|
20² =
12² + 16² 2020² =
1212² + 1616² 202020² = 121212² +
161616² … |
Normal,
les triplets
suivants sont des multiples du premier. |
||||||||||
|
Note 73
= 18² + 18 + 1 = 343 |
||||||||||
|
|
|
||||||||||
|
203 = 40² + 80² = 16² + 88² |
|
||||||||||
|
203 = 113 + 123 + 133
+ 143 = 8 000 |
|
||||||||||
|
203
= 8 000 = (2 + 3 + 4 + 5 + 6)3 = 113 + 123 + 133
+ 143 |
|
||||||||||
|
220 = 1 048 576 => 157 premier |
|
||||||||||
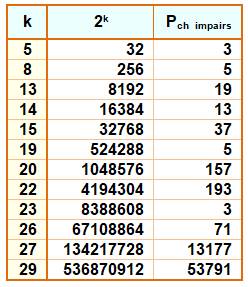
Puissances de 2 dont la suite des nombres impairs est un premier
|
Pour
k de 2 à 30 (Voir exemple ci-dessus)
|
Pour
de plus en plus de chiffres dans le
nombre premier: [5, 1],
[13, 2], [20, 3], [27, 5], [33, 6], [39, 7], [40, 9], [73, 12], [118, 15],
[150, 21], [209, 30], [344, 55], [434, 66], [824, 133] Exemple:
[27, 5] 227
= 134 217 728 13177 est premier avec cinq chiffres. |
Dénombrement, jeux et curiosités
|
1,
6, 15, 20, 15, 6, 1
|
|
|
20 |
|
|
20
= 4 x 5 x 6 / 6 |
|
|
|
|
|
20
= 12 + 3 – 45 + 67 – 8 – 9 |
|
|
20 =
5 + 5 + 5 + 5
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2,
[1, 0, 1, 0, 0] 3, [2, 0, 2] 4,
[1, 1, 0] 5, [4, 0] 6,
[3, 2] 7,
[2, 6] 8,
[2, 4] |
9, [2, 2] 10,
[2, 0] 11,
[1, 9] 12,
[1, 8] 13,
[1, 7] 14,
[1, 6] |
15,
[1, 5] 16,
[1, 4] 17,
[1, 3] 18,
[1, 2] 19,
[1, 1] 20,
[1, 0] |
9,
[2, 2] 19,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite |
|
|
Cette page |
![]()