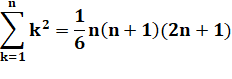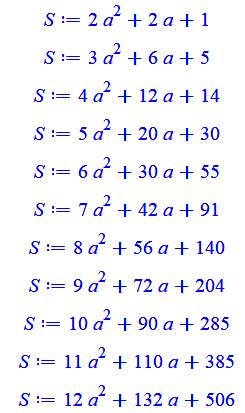|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Somme de CARRÉS consécutifs = CARRÉ On
connait la somme des entiers
aux carrés de 1 à n. On généralise à
la somme des entiers aux carrés de m à n et on cherche si de telles sommes sont
des carrés.
On trouve:
|
Anglais Sum of
consecutive squares equal to a square
Mise en bouche: somme de 12 entiers
consécutifs, jamais carré
|
Somme
de 12 nombres consécutifs: S(12) = n + (n+1) + (n+2) + … + (n
+11) = 12n + ½ 11 x 12 = 12n + 66 = 6 (2n + 11) La
somme S ne sera un carré que si (2n + 11) est un multiple de 6, or ce n'est
pas le cas, car ce nombre est impair. C'est
le cas également pour la somme de 4 entiers: S = 2 (n + 3), car (n+ 3) ne
peut pas être multiple de 2. Premières sommes carrées selon la quantité de termes 2(4,9)
/ 3(2,9) / 4(-) / 5(3,25) /
6(11,81) / 7(4,49) / 8(1,36) / 9(5,81) / 10(18,225) / 11(6,121)
/ 12(-) / 13(7,169) / 14(81,1225) / 15(8,225)
… Ex: 5(3, 25)
=> 3 + 4 + 5 + 6 + 7 = 25 = 5² 7(4,49)
=> 4 + 5 + 6 + 7 + 8 + 9 + 10 = 49 = 7² Notez (en rouge) la somme est le carré de
la quantité k de termes. Ce sont tous les cas pour k impairs. Avec
5 termes: S = 5n + 10, il suffit que n = 3 pour obtenir un carré: 5x3 + 10 =
25 = 5². La forme générique est: S = (2k-1)n + (2k-1)(k-1) ou avec n = k
=> S = (2k – 1) (k + k – 1) = (2k –
1)². Un carré. |
|
Aussi: quelques Repdigits sommes de
carrés de nombres consécutifs: 1 111 = 11² + 12² + 13² + 14² + 15² + 16² 44
444 = 71² + 72² + …+ 78² 444
444 = 51² + 52² + …+ 113² Ces
configurations sont rares, sans doute les seules. |
Voir Somme
des entiers / Somme
des entiers consécutifs /
Divisibilité
de la somme des entiers consécutifs
|
|
|||
|
Somme des entiers au carré à partir de 1 En 1875, Lucas se
pose la question: est-ce qu'une
pyramide à base carrée peut contenir une quantité carrée de boulets de canon?
Autrement-dit, est-ce que l'équation diophantienne: 1² + 2²
+ 3² + … + n² = C² a des solutions. Lucas affirmait que les seules solutions étaient n = 1 (trivial)
et n = 24 (dont la somme vaut 70² = 4 900). La preuve date de 1918 par
Watson. Départ quelconque Dans le cas de carrés consécutifs de
m à n, on connait par exemple: Il existe une infinité de telles
solutions, mais très "dispersés" (densité zéro). Si on trouve une solution avec k
termes consécutifs, k n'étant pas un carré, on peut en déduire une infinité
d'autres solutions (Laurent Beeckmans). |
Exemples
La première égalité est la seule en commençant par 1. Suite de cette liste Cette liste continue avec pour premiers termes: 304, 353, 540, 956, 1
301, 2 053, 3 112, 3 597, 5 448, 8 576, 12 981, 20, 425, 30 908, 35 709, 54
032, 84 996 … Négatifs Un départ négatif fonctionne également: - 4, -8, -11, -12, -15, -19,
-24, -32, -43, -48, -67, -99, … Avec -4, S = 16 + 9 + 4 + 1 + 0 + 1 + 4 +
9 + 16 + 25 + 36 + 49 +…+ 361 = 2500 =
50². Notez la répétition de certains carrés. À partir de – 24, on retrouve le nombre final de la somme en positif. |
||
|
Programme
Maple pour sommes de 24 carrés |
Commentaires Réinitialisation
générale. Initialisation
d'une liste L. Lancement
d'une boucle faisant progresser n le départ de la somme. Calcul
de la somme des carrés avec k l'indice qui fait passer aux nombres
consécutifs à partir de n. Test
si cette somme est un carré. Si oui, la liste L est complétée par la valeur
de n conduisant à un carré. En
bleu, le résultat du traitement. |
||
|
|
|||
|
Liste a = premier de k
termes pour une somme carrée par quantité croissante de carrés |
Légende
Lecture |
||
|
Programme
Maple pour première somme de carrés
|
Commentaires Même
programme que ci-dessus. Alors
que le précédent recherchait une somme de 24 termes celui- ci recherche les
sommes de kk termes. Alors
que le précédent énonçait plusieurs sommes, celui-ci s'arrête à la première
trouvée (break). En
bleu, le résultat du traitement. |
||
|
|
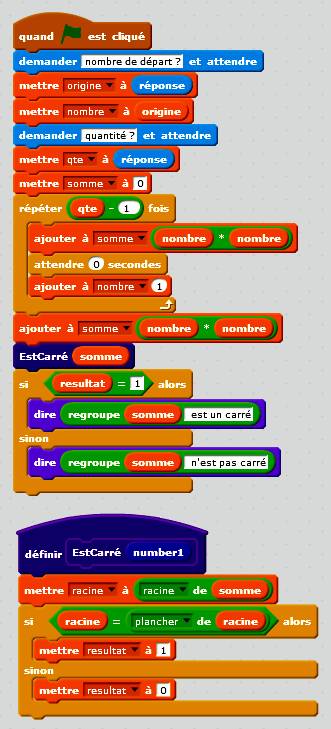
But Ce
programme teste si la somme de carrés est un carré. On donne le nombre de
départ et la quantité de carrés à ajouter. Résultat (exemple)
Commentaires Après
la phase d'initialisation des variables, à la huitième ligne, on lance le
calcul de la somme des carrés (nombre x nombre). La variable nombres est
incrémentée à chaque passage. Pour mieux visualiser cela, il est possible de
demander d'attendre quelques secondes à votre gré. La
somme est finalisée avec la dernière valeur de nombre. Appel
au bloc EstCarré défini en bas. Il teste si le nombre est un carré et
retourne résultat égal à 1 si oui et à 0 sinon. Les
dernières lignes affichent le message que prononce le chat. |
||
Voir Programmation – Index
|
|
|||
|
Pour commencer examinons le cas de cinq termes
dans la somme. Comme: Théorème La somme des
carrés de cinq nombres consécutifs n'est jamais un carré. |
Somme de cinq carrés
|
||
|
De façon
générale: |
S = (n – 2)² + (n – 1)² +
n² + (n + 1)² + (n + 2)² S = (n – 2)² + (n + 2)² +
(n – 1)² + (n + 1)² + n² S = 2n² + 8 + 2n² + 2 +
n² S = 5n² + 10 S = 5 (n² + 2) |
||
|
La somme
S n'est carré que si n² + 2 est un
multiple de 5. |
n² + 2 se
termine par 5 ou 0. n²
se termine par 3 ou 8. |
||
|
Propriété
des unités
des carrés |
Un
carré se termine par: {0, 1, 4, 5, 6, 9} Jamais par 3 ou 8. La somme de ces cinq carrés n'est jamais un
carré. |
||
|
Nous
venons de voir une méthode de démonstration particulière. La
méthode générale consiste:
Si
aucun des restes r ne se trouvent
dans la liste des restes des carrés, la somme
n'est pas un carré. |
|
|
||
|
Somme
des carrés de 1 à n: |
|
|
|
Somme des
carrés successifs de n = a jusqu'à n = a + k – 1, soit k termes à partir de
a. |
S
= a² + (a + 1)² + (a + 2)² + … + (a + k – 1)² S
= a² + a² + 2a + 1 + a² + 4a + 4 + … + (a + k – 1)² Somme des a² => ka² Somme des a => k (k – 1) a Somme des carrés => notre formule S =
ka² + k(k – 1)a + 1/6 (k – 1) k (2k – 1) |
|
|
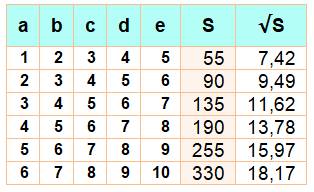
Valeur de
ces sommes pour k de 2 à 12 Exemple S(k = 5, a = 4) =
5x4² + 20x4 + 30 = 190 À
comparer à la valeur calculée dans le tableau du dessus. |
|
|
|
|
||
|
Pour k =
3 Voir Table des
restes de la division des carrés qui commence par:
|
S = 3a² + 6a + 1/6 (2) 3 (5) = 3a² + 6a + 5 S = 3a (a + 2) + 3 + 2 Cette expression divisée par 3 donne les restes 0 + 0 + 2; le reste de
toute l'expression est égal à 2. On écrit:
En se reportant à la table des restes
des carrés divisés par 3, on constate que ce reste ne peut être que 0
ou 1. On écrit:
La valeur 2 n'est jamais le reste d'un carré divisé par 3,
l'expression S ne peut jamais être un carré. La somme des carrés de trois
nombres consécutifs n'est jamais un carré. |
|
|
Pour k =
4 |
S = 4a² + 12a + 1/6 (3) 4 (7) = 4a² + 12a +
14 S = 4a (a + 3) + 12 + 2
La somme des carrés de quatre
nombres consécutifs n'est jamais un carré. |
|
|
|
||
|
Pour k =
5 |
Voir la méthode 1 ci-dessus >>> |
|
|
Méthode 2 |
S = 5a² + 20a + 1/6 (4) 5 (9) = 5a² + 20a +
30 S = 5(a² + 4a + 6) S n'est un carré que si la parenthèse est divisible par 5. P = a² + 4a + 6 = a (a+4) + 6 Jamais divisible par 5. La somme des carrés de cinq
nombres consécutifs n'est jamais un carré. |
|
|
Méthode 3 Nous allons utiliser cette méthode pour les valeurs suivantes de k
sans expliciter le détail du calcul. |
S = 5a² + 20a + 30 Avec k = 3 nous avions utilisé
la division par 3 et celle par 4 pour k = 4. Ici, la division par 5 ne marche
pas: elle donne un reste nul. Or, il existe des carrés qui, divisés par 5,
donnent un reste nul. Pas de conclusion possible. Essayons la division par 4.
Tous les cas seront couverts si on analyse l'expression pour a valant
(0, 1, 2 et 3), les quatre valeurs possibles du reste de la division par 4. S(a = 0) = 30 => reste 2 S(a = 1) = 5 + 20 + 30 = 55 => reste 3 S(a = 2) = 20 + 40 + 30 = 90 => reste 2 S(a = 3) = 45 + 60 + 30 = 135 => reste 3
Intersection
vide entre ces deux ensembles. Même conclusion: pas de carré avec cinq termes. |
|
|
|
|||
|
Sommes |
Se reporter au tableau ci-dessus >>> |
||
|
Intersection vide ? |
Pour chaque expression de la somme, on cherche la valeur de l'ensemble
S (ensemble des restes ou des congruences) mode d. Il s'agit de trouver une valeur de d produisant une intersection vide
avec C, lequel est l'ensemble des restes des carrés divisés par d. |
||
|
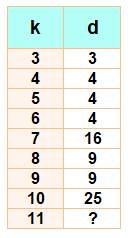
Valeurs trouvées |
Ce tableau montre
que: La somme des carrés de 3,
4, …10 nombres consécutifs n'est jamais un carré. Par contre pour 11, il existe des solutions: 18² + 19²
+…+ 28² = 77² 38² + 39²
+ …+ 48² = 143² 456² +
457² + …+ 466² = 1 539² 854² +
855² + … + 864² = 2 849² |
|
|
|
|
||
|
|
Commentaires Réinitialisation générale. Boucle en k, la quantité de termes de la somme. Boucle en d, pour la recherche du premier
diviseur provoquant une intersection vide. Initialisation de deux ensembles. Boucle d'exploration des valeurs de a, les restes
de le division par d. Calcul de la somme avec les valeurs des
paramètres k et a. La liste L est complétée par le reste de la division de S par d (S mod d). La liste LL est complétée par le reste de la
division du carré par d. En fin d'exploration si les deux listes n'ont
aucun élément en commun, on imprime la valeur de d trouvée et on stoppe le
balayage (break) pour passer à la valeur de k suivante. En bleu, le résultat du traitement. |
|
Voir Programmation – Index
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()