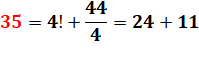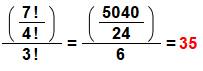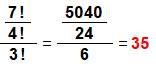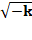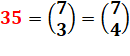Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 15/11/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	30	31		32	33		34	35	36	37	38	39

Nombre 35

Maths générales du 35

Maths détaillées du 35

Expressions 35

Trente-cinq

Thirty-five

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	10 0011
Bases	556
Romain	XXX V

Suite

35 = (10 – 3) (10 – 5)

Caractérisation du nombre

Balancé

Binaire équilibré (autant de "0" que de "1")

Binomial

Brillant

Complémenté

Composé

Composé inévitable (ou minimal)

Coster

Cunningham

Déficient

Impair

Qpart(6)

Queneau

Semi premier

Simple

Stirling 1

Van der Waerden

Cubique centré

Pascal

Pentagonal (5^e)

Pentatope

Pyramide triangle (5^e)

Tétraédrique (5^e)

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

CARTE D'IDENTITÉ
Nombre	Composé	Département	ILLE ET VILAINE
Facteurs	35 = 5 x 7	Élément	BROME Br
Pté Typique	35 = (10 – 3) (10 – 5)	Mnémo	MÂLE
	Suite Maths		Suite Culture

PROPRIÉTÉS Générales

Nombre	35 paires de premiers jumeaux jusqu'à 1 000.	>>>
	LCS 35 un défi datant de 1999, résolu en 2019.	>>>
Unité	Un arpent valait de 35 à 50 ares selon les localités.	>>>
Jeux	Il existe 35 hexominos.	>>>
Géométrie	35 triangles dans l'hexagone quelconque avec diagonales.	>>>
	35 intersections de diagonales dans l'heptagone	>>>

Géographie	35 sommets de la chaîne du Karakorum dont 10 de plus de 7 000 m. Le K2 (8 611m), sommet de cette chaîne, est le deuxième plus élevé du monde, soit 235 m de moins que le plus haut, l'Everest (8 846). Note: La quantité 35 est tirée d'un ouvrage; cependant, il est possible de donner le chiffre que l'on veut en fixant une altitude limite. Voir site Liste des sommets	>>>
	35 km Épaisseur moyenne de la croûte terrestre. Réduite à 10 km sous les océans.	>>>
Économie	En 1997, la France est le 35^e partenaire commercial de l'Inde.	>>>
Sciences	35 espèces de félidés. Chats, panthères, tigre, lion, guépard …
Politique	Sénateur: 35 ans au moins pour être éligible jusqu'en 2003; 30 ans depuis.	>>>
Finance	Un baril de pétrole fait l'objet de transactions financières 35 fois plus importances que sa réalité physique (ordre de grandeur).	>>>
Social	35 heures La semaine de travail en France.	>>> >>>
	35 meurtres par jour (12 632 en 2009) aux États-Unis. En France, c'est 680 assassinats en 2009, presque 2 par jour.
Construction	Les 35 arches du pont du Gard.	>>>
Transport	35 minutes Durée du trajet Eurostar dans le tunnel sous la Manche avec des pointes à 130 km / h pour 50,4 km.	>>>
	35 secondes dans les embouteillages …	>>>

Littérature	Latude ou Trente-Cinq Ans de captivité - René Charles Guilbert de Pixerécourt - 1834	>>>
	Corneille a écrit 35 pièces: Le Cid, Horace …
Référence	35 tomes Grande Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers (1751-1772) - Diderot et d'Alembert.	>>>
Chanson Musique	Deux minutes trente-cinq de bonheur – Sylvie Vartan.
Cinéma	35 mm: largueur de la pellicule cinéma. Bobines de film de 35 millimètres.	>>>
Religion	35 ans Âge de l'Éveil du Bouddha (» 525 av. J.-C. ). Sa prédication commença par le Sermon de Bénarès et se poursuivit pendant 35 ans à travers l'Inde du Nord-Est.	>>>

Autour du nombre

Nombre	35,4°	35,4107392…° = 35° 24' 38"… = 0,618 … radians Valeur de l'angle correspondant à l'inverse du nombre d'or	>>>
Transport	35,5	35,5 km Longueur du périphérique parisien.	>>>
Océanographie Maritime	0,035	35 ‰ (35 pour 1000) Salinité de l'eau des océans.	>>>

Propriétés MATHÉMATIQUES

Chiffres et numération

35 + 53 = 88 35 × 5 × 3 = 525	Devient palindrome en lui ajoutant son retourné ou par multiplication avec ses chiffres.
353637 = 39293 x 9	Palindrome et trois nombres successifs concaténés.
35 x 37 x 39 = 50 5 05 35 + 37 + 39 = 111 & 50 5 05 / 111 = 455	Curiosité: trois nombres en progression de 2 Qui forment des palindromes.

Addition et soustraction

35 = 2 + 3 + 4 + 5 + 6 + 7 + 8 = 5 + 6 + 7 + 8 + 9 = 17 + 18		Trois seules sommes de nombres consécutifs >>>
35 = 5 + 6 + 7 + 8 + 9	Partition unique avec cinq chiffres différents, parmi 14 883 partitions pour le nombre 35.
1+2+3+…+34 = 595 / 35 / 36+37+…+49 = 595	Somme égale de part et d'autre du 35. Problème de la maison du maire.
35 = T1 + T2 + T3 + T4 + T5 = 1 + 3 + 6 + 10 + 15	Somme de nombres triangulaires consécutifs. Nombre tétraédrique.

Multiplication, division, diviseurs

35 = 5 x 7		Nombre simple. Nombre composé. Nombre égal à sept fois ses unités.
35 = 5 x 7 3x2 = 6 et 5		Ses deux facteurs sont une paire de nombres premiers jumeaux. Produit de deux nombres premiers successif et concaténation de deux nombres dont l'un est le double moins 1 de l'autre. Rare.
		Le produit de quatre nombres consécutifs est divisible par 24. Tous ces nombres figurent dans la cinquième diagonale du triangle de Pascal.
35 = (10 – 3) (10 – 5) = 7 x 5			Nombre complémenté
35 = 7! / (3! x 2)² = 7! / 12² = 5040 / 144			Factorielle divisée.
35 = 7! / 4! 3! = 5 040 / 24 x 6 = 5 040 / 144			Avec des factorielles.
	Le totient de ce nombre est factoriel. Liste: 1, 3, 7, 35, 143, 779, 5183, 40723, 364087, 3632617, 39916801, 479045521, 6227180929, 87178882081, 1307676655073, 20922799053799, … OEIS A022487 Erdös et Gupta pensent que phi(x) = n! a une solution pour tout n.

Avec les puissances

35 = 1² + 3² + 5² = 1² + 3² + 3² + 4² = 1² + 1² + 1² + 4² + 4² = 1² + 1² + 2² + 2² + 5² = 2² + 2² + 3² + 3² + 3² = 2^3 + 3^3 = 1^4 + 1^4 + 1^4 + 2^4 + 2^4 = 1^5 + 1^5 + 1^5 + 2^5	Toutes les sommes de puissances de 2 à 5 avec deux à cinq termes.
35 = 18² – 17² = 18 + 17	Motif général pour tout nombre impair.
35 = 6² – 1²	Voir Autour de 12345.
35 = 2^3 + 3^3 = 8 + 27 = 5 x 7	Nombre binomial. Somme de deux cubes de nombres successifs: n^3 + (n+1)^3. Elle est toujours divisible par (2n+1). Somme des cubes de deux premiers consécutifs.
35 = 2^3 + 3^3 = 5 x 7 = (2+3) (2² - 2x3 +3²)	La somme de deux cubes est toujours le produit de deux nombres (identité remarquable).
11 = 2^1 + 3^2 = 2^3 + 3^1 35 = 2^3 + 3^3 = 2^5 + 3^1 259 = 2^8 + 3^1 = 2^4 + 3^5	Deux fois en 2^a + 3^b. Sans les trois nombres de cette forme avec deux présentations.
6^2 – 1 = 35 6^4 – 1 = 1295 6^6 – 1 = 46655 …	Toutes les puissances paires de 6, moins 1, sont divisibles par 35.

En puissance

35^2 = 1225 335² = 112225	Motif itératif sans fin.
(35² + 36²)² = 1456^3 – 1455^3 = 6 355 441	Curiosité avec des nombres successifs. Même chose avec 9, 35, 132.
35^2 = 5² × 7² = 1^3 + 3^3 + 5^3 + 7^3 + 9^3	Carré somme de cubes successifs.
35^3 = 42 875 38^3 = 54 872	Motif avec permutation des chiffres sur deux cubes.
35^4 = 4^4 + 21^4 + 22^4 + 26^4 + 28^4= 14^4 + 14^4 + 21^4 + 28^4 + 28^4	Bicarré sommes de cinq bicarrés. dont la 2^e comme multiple de: 5^4 = 2^4 + 2^4 + 3^4 + 4^4 + 4^4
35^5 = 52 521 875 & 5+2+5+…+7+5 = 35		Nombre NESCHIP.
35^9 = 78815638671875 => 7+8+8+…+5 = 80 80^9 = 134217728000000000 => 1+3+4+…+0 = 73		Motif en couple.

Dénombrement, jeux et curiosités

35 = ½ ( 3 x 5² – 5) 35 = 1 + 4 + 7 + 10 + 13	Cinquième Nombre pentagonal. Nombre pentatope.
35 = (5 x 6 x 7) / 6	Nombre tétraédrique (5^e). Somme des premiers nombres triangulaires.
35 x 15 873 = 555 555	Plus petit repdigit multiple de 35. Objet d'une multiplication ingénieuse.
35 = (5) (5 + 1) (5 + 2) / 6 = 5 x 6 x 7 / 6	Nombre pyramide triangle.
1 + 2 + … + 34 = 36 +… + 49 = 595	Somme égale de part et d'autre de 35.
	Jeu du quatre 4.
	Coefficient du binôme ou nombre de Pascal. Combinaisons de 7 objets pris 3 par 3 ou 4 par 4.

3,5 5,7 11,13 …

827, 829 857, 859 881, 883

Il y a 35 paires de nombres premiers jumeaux jusqu'à 1000.

Voir la barre magique des nombres premiers.

Nombre d'hexominos, chacun formés de 6 carrés.

Voir Hexominos

Le nombre de classe de ce corps quadratique est 2.

Ce corps contient tous les nombres de la forme a + ib avec a et b rationnels. Il existe 18 tels corps avec k = 5, 6, 10, 13, 15, 22, 35, 37, 51, 58, 91, 115, 123, 187, 235, 267, 403, 427. OEIS A005847 / Table

Autour du nombre

F35 = 9 227 465 et 9+2+2+7+4+6+5 = 35		La somme des chiffres du 35^e nombre de Fibonacci est égale à 35.
35	Quantité de possibilités de classer les chiffres de 1 à 7 en deux ensembles dont chacun contient au moins trois chiffres. Quantité de façons de repartir 7 balles dans deux paniers avec trois balles minimum dans chaque panier.
UN => 21 + 14 = 35		UN est le nombre qui a la plus petite masse.

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 0, 0, 0, 1, 1] 3, [1, 0, 2, 2] 4, [2, 0, 3] 5, [1, 2, 0] 6, [5, 5] 7, [5, 0] 8, [4, 3]	9, [3, 8] 10, [3, 5] 11, [3, 2] 12, [2, 11] 13, [2, 9] 14, [2, 7]	15, [2, 5] 16, [2, 3] 17, [2, 1] 18, [1, 17] 19, [1, 16] 20, [1, 15]	6, [5, 5] 34, [1, 1]

Voir Bases / Brésiliens

Suite	Voir le menu en haut de page Nombre 36
Voir	Cristaux Cycle de vie Grille magique Palindrome retard Primorielle
Aussi	Solitaire
Site	Références Internet
Cette page	http://villemin.gerard.free.fr/NombDico/Nb30a50/Nb35.htm