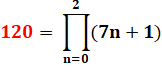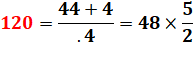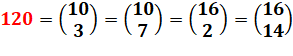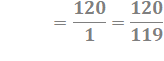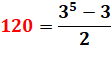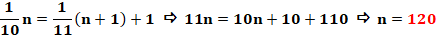dictionnaire des nombres – 120, cent vingt

Édition du: 06/11/2024

M'écrire

Brèves de Maths

DicoNombre

Débutant

Glossaire

Types de nombres

Nombres géométriques

Nom des nombres

Écriture des nombres

Table des facteurs

Nombres et anglais

Langues

Dictionnaire des Nombres

1 / 10 / 50 / 70 / 80 / 90 / 95 / 96 / 97 / 98 / 99 / 100 / 101 / 102 / 103 / 104 / 105 /106 / 107 / 108 / 109 / 110 / 111 / 112 / 113 / 114 / 115 / 110 / 115 / 116 / 117 / 118 / 119

120

121 / 122 / 123 / 124 / 125 / 126 / 127 / 128 / 129 / 130 / 131 / 132 / 133 / 134 / 135 / 140 / 150 / 200 / 250 / 300 / 400 / 500 / 1000 / Autres

Soyons sobres! 120, C 100'H, 10 20 100.

Sans vin, c'est sans tache, dit Vincent.

Par ma foi, je disais cent ans, mais vous passerez les six-vingts.

Frosine dans l'Avare de Molière (acte II, scène 5)

à Harpagon en le flattant sur sa longévité.

Voir Pensées & humour / Alphabet parlant

Cent-vingt

One hundred (and) twenty

Orthographe / Langues

Facteurs
Diviseurs	1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
Quantité	16 = 2⁴
Somme	360 = 3 x 120
Binaire	111 1000
Romain	CXX

Suite en propriétés arithmétiques

En anglais, hundred signifiait 120, issu du vieux scandinave (hundrath) du fait d'un système de numération duodécimal.

120 est un nombre triangulaire de 15 rangées

5 - bonacci

Abondant

Abondant (hautement -)

Abondant (super -)

Admirable

Ami avec 672

Brésilien (hautement)

Composé (hautement)

Congruent

Constructible

Diviseur en puiss. de 2

Dihédral

Docile (amenable)

Euler – Permutations

Factorielle

Factorielle tronquée

Faiblement totient

Fourchette ou gapful

Harshad

Idonéal

Interpremier

Intouchable

MulQprem

Multi-pronique

Nombre de Pascal

Pair

Pratique

Semi-parfait

Stirling 1

Triparfait

Zumkeller

Géométrique

Hexagonal

Nombre tarte

Pascal

Pyramide triangle (8^e) ou tétraédrique

Triangulaire (15^e)

120 était connu comme le grand cent (Hundert) alors que 100 était le petit cent dans le monde Teutonique avant 1700.

Autrefois, on disait aussi six-vingts pour 120.

120 : one hundred twenty in American English; written and spoken as one hundred and twenty in British English and other english forms.

Voir Nombres en anglais

Géométrie	120° Angle interne de l'hexagone régulier. Angle du plus court chemin entre 3 points. Angle caractéristique en cristallographie. Nombre de symétries du dodécaèdre et de l'icosaèdre.	Chemin court Chemin d'Euler
	120° Résolution d'un fameux triangle algébrique		>>>
Jeux	120 cartes de 10 couleurs d'un jeu de cartes indien. Un des plus vieux (dasavatara). Dix couleurs comme les dix avatars de Vishnu.		>>>
	120 Constante d'un carré magique multiplicatif.		>>>
Sport	120 m Record de plongée par Arnaud Jerald le 9 aout 2022. Record absolu en poids constant bi-palmes.		>>>
Géographie	120 fuseaux UTM Découpe de la surface de la Terre en 60 fuseaux de 6 degrés dans l’hémisphère Nord et idem au sud. La France se situe sur les fuseaux 30, 31 et 32.		>>>
	120 est le coefficient de marée maximum.		>>>
Cosmologie	120 km / s = 430 000 km/h. Vitesse de rapprochement de la galaxie Andromède par rapport à notre Galaxie, la Voie Lactée. Collision dans quatre milliards d'années. En fait: coalescence, c'est-à-dire: fusion des galaxies en une future galaxie nommée: Milkomède ou Lactomède.		>>>
Militaire	120 pas par minute cadence normale de la marche au pas militaire (88 pour les légionnaires).
Défense	120 km Portée du canon dit "Grosse Bertha" fabriqué par Krupp durant la première guerre mondiale. Obus de 1 tonne sur Paris en 1918.
Littérature	Les 120 journées de Sodome Roman de Sade (1782-1785), écrit à la prison de la Bastille en 1785 et publié en 1904. Note: on écrirait le titre en toutes lettres aujourd'hui.	Romans et nombres
Chimie	120 molécules Nombre de types de molécules organiques simples différentes dans l’espace interstellaire. On a détecté des molécules complexes allant jusqu’à 15 atomes. Il est prouvé que l’eau est présente sur certaines planètes. Janvier 2000

Chiffres et numération

120 + 021 = 141 120 – 021 = 99	Devient palindrome en lui ajoutant son retourné, et repdigit en lui retirant.
120₁₀ = 1320₄ = 64 + 3x16 + 2x4	Pannumérique en base 4. Notez le 3 qui s'intercale dans 120.
120 = [10, 10]₁₁ = 88₁₄ = 66₁₉ = 55₂₃ = 44₂₉ = 33₃₉ = 22₅₉	Multi repdigit record avec 8 configurations. Nombre brésilien 7 fois.
120 / (1 + 2 + 0) = 40	Nombre de Harshad.

Addition et soustraction

120 = 4 + 8 + 16 + 31 + 61

Nombre 5 - bonacci.

120 = T₁₅ = 1/2 (15 x 16)

= 4 x 5 x 6

= 2 x 3 x 4 x 5

= 1 x 2 x 3 x 4 x 5

Nombre triangulaire (15^e).

L'un des six nombres triangulaires, produit de trois nombres consécutifs.

Seul nombre triangulaire, produit de quatre nombres consécutifs, et même, cinq.

Seul nombre avec 6 à être triangulaire et factoriel.

120 = 1 + 2 + 3 + 4 + 5 +...+ 14 + 15

= 1+3+6+10+15+21+28+36

= (8 x 9 x 10) / 6

= (15 x 16) / 2

Une des trois sommes de nombres consécutifs >>>

Nombre pyramide triangle.

Tétraédrique (8^e). Somme des nombres triangulaires successifs.

Un des cinq nombres à la fois triangulaire et tétraédrique.

Nombre hexagonal (8^e).

Voir Brève 660

120 = T₁ + T₂ +…+ T₈ = T₁₅

Triangulaire, somme de nombres triangulaires.

120 = 59 + 61

= 23 + 29 + 31 + 37

Somme de deux premiers jumeaux.

Somme de premiers consécutifs.

Multiplication, division, diviseurs

120 = 2³ × 3 × 5		Facteurs
120 = 2 × 3 × 4 × 5 = 4 × 5 × 6 210 = 5 × 6 × 7 = 14 × 15 720 = 2 × 3 × 4 × 5 × 6 = 8 × 9 × 10		Double produit de nombres consécutifs. Plus petit cas. Liste: 120, 210, 720, 5040, 175560, 17297280, 19958400, 259459200, 20274183401472000, … OEIS A064224
113, 120, 127	Interpremier avec nouveau record (7) d'écart.
Diviseurs de 120 = {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120}.	Ils sont 16 = 4² = 2⁴, un carré et un bicarré. En rose, les deux diviseurs supplémentaires par rapport à 60. Voir Base 60
120 = 6! / 3!	Nombre quadri-factorielle (de la forme 2n! / n!), comme: 12, 120, 1680, 30240, … OEIS A001813
120 = 2 x 3 x 4 x 5 = 11² – 1 = 10 x 12	Produit de quatre nombres consécutifs. Propriété générale. Deux fois produit de nombres consécutifs. Le plus petit cas: Liste: 120, 210, 720, 5040, 175560, 17297280, 19958400, 259459200, … OEIS A064224
120 (n-2) (n-1) n (n+1) (n+2) Ex: 5x6x7x8x9 = 15120= 120 x 126	Le produit de 5 nombres consécutifs est divisible par 120.
120 (n⁵ – 5n³ + 4n) si n 2 Ex: 3⁵ – 5 x 3³ + 4 x 3 = 120 4⁵ – 5 x 4³ + 4 x 4 = 720 = 120 x6	Cette expression est divisible par 120.

120 = 2³ x 3 x 5

= 2 x 3 x 4 x 5

= 1 x 2 x 3 x 4 x 5 = 5!

= 6! / 3!

Factorielle.

Factorielle terminée par un 0 du fait du produit de 2 par 5.

Nombre triangulaire égal à une division de factorielles.

120 = 1 x 2 x 3 x 4 x 5

Factorielle classique (1-uple) de 5.

      Factorielle septuple de 2
   = (7x0+1) (7x1+1) (7x2+1)
   = 1 x 8 x 15

Expression des factorielles avec somme de puissances.

1 x 2 x 3 = 6

120 = 4 x 5 x 6

7 x 8 x 9 = 220 + 284

Factorielle tronquée. Produit de 3 nombres consécutifs. Nombre multi-pronique.

Divisible par 24 comme tout produit de trois nombres consécutifs dont le central est impair.

Trois beaux produits avec la suite des nombres: 6 étant un nombre parfait; 120 un triparfait; et 220 + 284 la somme d'une paire amiable.

2 x 60 = 120

3 x 40 = 120

4 x 30 = 120

5 x 24 = 120

6 x 20 = 120

8 x 15 = 120

10 x 12 = 120

Plus petit nombre sept fois produit de deux nombres.

120 = 6 x 20

120 – 1 et 120 + 1 sont composés

Premier nombre orphelin. Le plus petit multiple de 6 avec 6n 1 qui sont tous deux composés.

Il y a 30 nombres premiers inférieurs à 120 et, 120 est multiple de 30. Aucun nombre n'a 120 pour somme de diviseurs.	Nombre MulQprem. Nombre Intouchable.
120 a 16 diviseurs. Somme diviseurs = 360 = 3 x 120	Hautement composé; le plus petit avec autant de diviseurs. Nombre triparfait. Le plus petit nombre ayant 16 diviseurs en 2^N. 120 a le même nombre de diviseurs que 210 (et, que bien d'autres).
120 = tau (55 440)	Quantité de diviseurs de 55 440, nombre hautement composé.
120	Nombre semi-parfait: 278 fois somme de certains de ses diviseurs.
120 et ses diviseurs {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120}	Forment un système de congruences qui couvre tous les entiers.
	Les sommes des carrés des diviseurs sont égales. Seules possibilités pour n + k avec k de 1 à 100.
	Nombre pour lequel cette puissance dépasse le nombre. La fonction oméga compte les facteurs uniques et oméga majuscule, les facteurs répétés.

Avec les puissances

120 = 2² + 4² + 10² = 2² + 4² + 6² + 8² = 1² + 2² + 3² + 5² + 9² = 1² + 3² + 5² + 6² + 7²	Sommes de carrés distincts.
120 = 11² – 1² = 13² – 7² = 17² – 13² = 31² – 29²	Différence de deux carrés.
49, 169, 289	Nombre congruum: trois carrés en progression arithmétique.
120 et puissance 5	La différence cinquième des puissances 5 est égale à 120 = 5!
120 = 3¹ + 3² + 3³ + 3⁴	Somme de puissances successives.
120 = 2⁷ – 2³ = 5³ – 5¹	Différence de puissances d'un même nombre.
120 = 11² – 1	Toutes les puissances paires de 11, moins 1, sont divisibles par 120.
120 = 11² – 1 = 100 + 20 = 4 x 5 x 6 = 10 x 12	Formes générales prise par le carré d'un nombre impair moins 1. Coquetterie en 4,5,6.

Dénombrement, jeux et curiosités

		Jeu du quatre 4. Avec la notation anglaise: .4 = 0,4 = 2/5
120 = 10! / (10-3)! x 3!			Le plus petit nombre six fois (dont deux cas triviaux) dans le triangle de Pascal. Combinaisons de 10 objets pris par 3 ou par 7; ou de 16 objets pis par 2 ou par 14.
120 = 5!	Quantité de permutations de 5 objets distincts. 12345 12354 12435 12453 12534 12543 13245 13254 13425 13452 13524 13542 14235 14253 14325 14352 14523 14532 15234 15243 15324 15342 15423 15432 Etc.
	Quantité de nombres jusqu'à 9 999 ne comportant que les chiffres 7, 8 ou 9. Ce sont: 7, 8, 9, 77, 78, 79, 87, 88, 89, 97, 98, 99, 777, 778, 779, 787, 788, 789, 797, 798, 799, 877, 878, 879, 887, 888, 889, 897, 898, 899, 977, 978, 979, 987, 988, 989, 997, 998, 999, 7777, 7778, 7779, 7787, 7788, 7789, 7797, 7798, 7799, 7877, 7878, 7879, 7887, 7888, 7889, 7897, 7898, 7899, 7977, 7978, 7979, 7987, 7988, 7989, 7997, 7998, 7999, 8777, 8778, 8779, 8787, 8788, 8789, 8797, 8798, 8799, 8877, 8878, 8879, 8887, 8888, 8889, 8897, 8898, 8899, 8977, 8978, 8979, 8987, 8988, 8989, 8997, 8998, 8999, 9777, 9778, 9779, 9787, 9788, 9789, 9797, 9798, 9799, 9877, 9878, 9879, 9887, 9888, 9889, 9897, 9898, 9899, 9977, 9978, 9979, 9987, 9988, 9989, 9997, 9998, 9999.

Autour du nombre

{1, 3, 8, 120}

xy + 1 = k²

Ensemble complet de nombres tels que xy + 1 est un carré quels que soient x et y différents pris dans cet ensemble.

Exemple: 120 x 8 + 1 = 961 = 31²

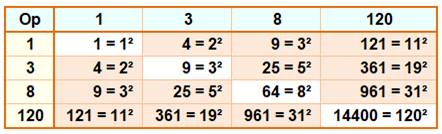
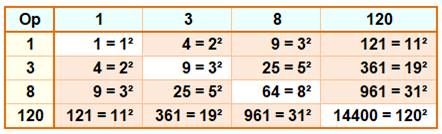
120, 8, 3, 1

Tous les nombres du tableau sont des carrés.

Op pour la diagonale = produit.

Op pour les autres = produit + 1.

120 = aire de 16 17 17

10 24 26

17 17 30

16 25 39

Aire de quatre triangles héroniens.

Question: quel est le nombre n tel que son dixième excède le onzième du nombre suivant d'une unité ?

Réponse:

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]

Repdigit (Brésilien)

120

2, [1, 1, 1, 1, 0, 0, 0]

3, [1, 1, 1, 1, 0]

4, [1, 3, 2, 0]

5, [4, 4, 0]

6, [3, 2, 0]

7, [2, 3, 1]

8, [1, 7, 0]

9, [1, 4, 3]

10, [1, 2, 0]

11, [10, 10]

12, [10, 0]

13, [9, 3]

14, [8, 8]

15, [8, 0]

16, [7, 8]

17, [7, 1]

18, [6, 12]

19, [6, 6]

20, [6, 0]

21, [5, 15]

22, [5, 10]

23, [5, 5]

24, [5, 0]

25, [4, 20]

26, [4, 16]

27, [4, 12]

28, [4, 8]

29, [4, 4]

30, [4, 0]

60, [2, 0]

11, [10, 10]

14, [8, 8]

19, [6, 6]

23, [5, 5]

29, [4, 4]

39, [3, 3]

59, [2, 2]

119, [1, 1]

Voir Bases / Brésiliens

Suite	Nombre 121 Autres nombres
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres
Site	Références Internet
Cette page	http://villemin.gerard.free.fr/NombDico/N100a500/Nb120.htm