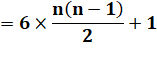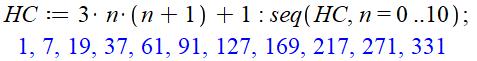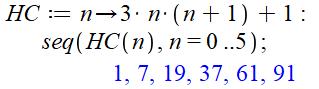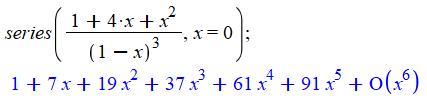NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 12/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres Figurés
Débutants Nombres figurés ou géométriques	Nombres géométriques				Glossaire Nombres géométriques
INDEX Nombres figurés	Triangle	Carré	Pentagonaux	Hexagonaux
		Étoilé	Pentagonaux centrés	Hexagonaux centrés
			En grappe pentagonale
		Sommaire de cette page >>> Nombres hexagonaux centrés >>> Propriétés

NOMBRES HEX

ou hexagonaux centrés

Quantités de billes placées aux sommets d'hexagones concentriques avec une bille au centre.

Anglais: Centred hexagonal numbers or hex numbers

Nombres HEXAGONAUX CENTRÉS

Exemple

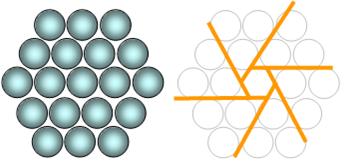
37 = 1 + 6 + 12 + 18

Quatrième nombre hexagonal centré.

Formules pour C_6,n

= n³ – (n – 1)³

= 3n² – 3n + 1

= C_{6, n–1} + 6(n – 1)

= 6 T_n–1 + 1

Centré ou non

Côté	Hexagone	Hexagone Centré
1	1	1
2	6	7
3	15	19
4	28	37

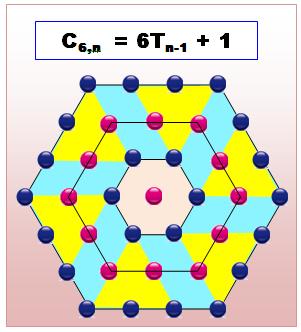
Calcul de la formule

Cette figure montre comment relier le nombre pentagonal aux nombres triangulaires (jaunes).

Liste des nombres HEX

Avec son rang

[1, 1], [2, 7], [3, 19], [4, 37], [5, 61], [6, 91], [7, 127], [8, 169], [9, 217], [10, 271], [11, 331], [12, 397], [13, 469], [14, 547], [15, 631], [16, 721], [17, 817], [18, 919], [19, 1027], [20, 1141]

Suite

… 1261, 1387, 1519, 1657, 1801, 1951, 2107, 2269, 2437, 2611, 2791, 2977, 3169, 3367, 3571, 3781, 3997, 4219, 4447, 4681, 4921, 5167, 5419, 5677, 5941, 6211, 6487, …

Programmation Maple

Autre forme (type fonction)

Polynôme générateur

Voir Polynômes générateurs des partitions

Propriétés

Unités

et

Dizaines

Les unités des HEX suivent le motif palindromique:

1, 7, 9, 7, 1

Les deux derniers chiffres suivent un motif palindromique de longueur 100.

1, 7, 19, 37, 61, 91, …, 91, 61, 37, 19, 7, 1<

Racine numérique

La somme itérée des chiffres (racine numérique) des HEX produit un motif palindromique

1, 7, 1

Moyenne = carré

La moyenne des HEX jusqu'à n est un carré:

[1, 7], 4

[1, 7, 19], 9

[1, 7, 19, 37], 16

[1, 7, 19, 37, 61], 25

[1, 7, 19, 37, 61, 91], 36

Somme = cubes

Rappel:

HC_n = n³ – (n – 1)³
= 3n² – 3n + 1

1	= 1	= 1^3
1 + 7	= 8	= 2^3
1 + 7 + 19	= 27	= 3^3
1 + 7 + 19 + 37	= 64	= 4^3
1 + 7 + 19 + 37 + 61	= 125	= 5^3
1 + 7 + 19 + 37 + 61 + 91	= 216	= 6^3
1 + 7 + 19 + 37 + 61 + 91 + ... + Hn		= n^3

Relation avec les nombres triangulaires HCn = 6 Tn-1 + 1
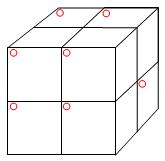
Relation avec les cubes géométriques	Soit un cube formé de n×n×n petits cubes. Les nombres HEX donnent la quantité maximale de cubes visibles à partir d'un point de vue fixe donné. Ici, avec 2x2x2, on peut voir seulement sept cubes (marqués en rouge)

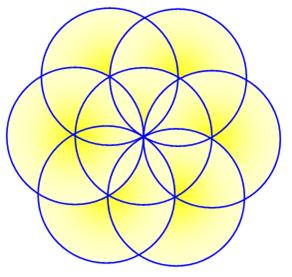
Rosace La quantité de cercles pour réaliser des rosaces de plus en plus grandes est un nombre HEX. Ici 7 cercles pour le premier niveau.

Partitions Les HEX donnent la quantité de partitions des nombres en 6n en utilisant les trois premiers nombres

Les 7 partitions de 6 avec 3 nombres [1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 2], [1, 1, 2, 2], [2, 2, 2], [1, 1, 1, 3], [1, 2, 3], [3, 3] Les 19 partitions de 12 avec 3 nombres [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2], [1, 1, 1, 1, 1, 1, 1, 1, 2, 2], [1, 1, 1, 1, 1, 1, 2, 2, 2], [1, 1, 1, 1, 2, 2, 2, 2], [1, 1, 2, 2, 2, 2, 2], [2, 2, 2, 2, 2, 2], [1, 1, 1, 1, 1, 1, 1, 1, 1, 3], [1, 1, 1, 1, 1, 1, 1, 2, 3], [1, 1, 1, 1, 1, 2, 2, 3], [1, 1, 1, 2, 2, 2, 3], [1, 2, 2, 2, 2, 3], [1, 1, 1, 1, 1, 1, 3, 3], [1, 1, 1, 1, 2, 3, 3], [1, 1, 2, 2, 3, 3], [2, 2, 2, 3, 3], [1, 1, 1, 3, 3, 3], [1, 2, 3, 3, 3], [3, 3, 3, 3].

Nombres géométriques		Introduction Valeurs Théorie
Voir	Dames chinoises Théorie des nombres géométriques Géométrie – Index Nombres centrés
Site	En savoir plus sur ces nombres géométriques et d'autres Figurate numbers d'Eric Weisstein Absolument intarissable sur le sujet OEIS A003215 - Hex (or centered hexagonal) numbers: 3*n*(n+1)+1
Livre	Pour développements complets, voir Conway et Guy " The book of numbers " (Le livre des nombres)
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/SeptHexC.htm