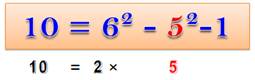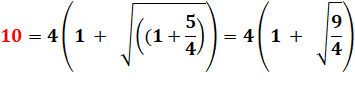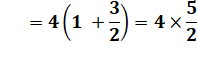nombre dix

Édition du: 20/07/2025

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10⁶ / 10⁹ / 10¹⁰⁰ / Infini
	-0-	10		20	30		40	50	60	70	80	90
	10	11		12	13		14	15	16	17	18	19

Nombre 10	Culture	Maths 10	Échelle de 10	Expressions en 10
Débutant 10	Culture 10	Opération 10	Science 10	Proverbes avec 10
Quiz 10	Pluriels détournés	Puissance de 10	Multi-puissance 10	Horloge maths

Dix

Ten

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1010
Bases	22₄ 11₉
Romain	X

Suite

Voir Partitions / Table des quantités

Caractérisation du nombre

Voir Nom des nombres / Nombres selon langues / Nombres selon bases / Fonctions arithmétiques

Caractère chinois (Kangi) pour 10

Ressemble à deux mains croisées,

chacune représentant le nombre 5.

Anticoïndicateur (le plus petit)

Base du système décimal

Brillant

Composé

Composé inévitable (ou minimal)

Constructible

Déficient n° 9

Dihédral

Équidigital

Harshad

Heureux

Idonéal

Pair

Perrin (8^e)

Semi-méandrique

Semi-premier

Simple

Stirling 1

Géométrique

Décagonal

Ennéagonal centré (2^e)

Pascal

Pyramide triangle (3^e)

Tétraédrique (3^e) =>

Triangulaire (4^e) =>

Triangulaire centré (3^e)

Rappel Propriétés générales >>>

Au début, avec ma femme, nous faisions l'amour dix fois par mois. Aujourd'hui, c'est plutôt une fois par moi … et neuf fois par les autres.

Desproges

Saint-Antoine de Padoue, dix de retrouvées.

Détournement de: une de perdue, dix de retrouvées par Jean Yanne

Anglais: there's plenty more fish in the sea

Différentes façons de compter jusqu'à 10.

On cherche un employé capable de compter jusqu’à 10.

Le premier candidat: 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 – C'est bien, mais dans le bon sens, maintenant. – Je ne sais pas, j’ai travaillé à la NASA.

Le deuxième candidat : 1, 3, 5, 7, 9, 10, 8, 6, 4, 2 – D'accord, mais dans le bons ordre. – Désolé, j’ai travaillé comme facteur et je ne sais pas compter autrement.

Le troisième candidat: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 – Parfait ! Vous êtes engagé. Pour information, savez-vus compter plus loin ? – Bien sûr: Valet, Dame et Roi !

Devinette

Vous entrez dans une pièce.
Deux chiens, quatre chevaux, une girafe et un canard sont couchés sur le lit.
Trois poussins volent au dessus d’une chaise.

Combien de pieds y a t’il au sol ?

Réponse: 4 pieds de lit + 4 pieds de chaise + 2 pieds de vous = 10.

Voir Pensées & humour

DIX

= 10 = 10¹

= 1 déca = 1 da (1 dam = 10 m)

Un DIXIÈME

= 1/10 = 10^-1

= 1 déci = 1 d (1 dm = 1/10 m = 10 cm)

Unités: 1 décamètre (dam): ruban de dix mètres servant à mesurer

1 décimètre ou double-décimètre: règle de 10 ou 20 centimètres.

1 décalitre (dal) vaut dix litres, le contenu d'un grand seau.

1 décanewton (daN): force proche d'un kilogramme-force.

Numération Notre système de numération est à base 10. Voir Système décimal

Il comporte 10 chiffres {0 1 2 3 4 5 6 7 8 9} Voir Pannumérique

Le chiffre des dizaines est le deuxième en partant de la droite:

Ex: N = 123456789 => dizaine = 8 => notée d = 8.
Anglais: Dizaine => The tens place

Ex: The digit in the tens place of a power of 7 is always 0 or 4

Langage Déca pour café décaféiné

Déci: un décilitre de vin, dans les cafés. Voir Contenances

Voir Notation des grands nombres / Échelle de dix / Orthographe

Devinette

Énigme classique pour les anglophones, souvent utilisée pour solliciter la pensée latérale (lateral thinking)

Avec une seule barre rétablir l'égalité:

Solution

Numération – Chiffres

10 10 = 1010₂ 20 = 10100₂ 40 = 101000₂ 80 = 1010000₂	Plus petit nombre à deux chiffres. Double ses chiffres en binaire. Le binaire contient le nombre. Vrai pour toutes les puissances de 10 Deux chiffres à "1" en binaire: nombre païen (evil number). Idem pour 20, 40, 80 ...
10₁₀ = 1010₂ = 101₃	Mêmes chiffres dans trois bases. Plus petit cas.
10₁₀ = 1010₂ = 2³ + 2¹ 10₁₀ = 22₄ = 2 (4¹ + 4⁰) 10 = 2/3 (4² – 1) = 2/3 x 15 = 2 x 5		Répétition de 10 en binaire. Somme des premières puissances impaires de 2. Repdigit en base 4. Double de la somme des premières puissances de 4.
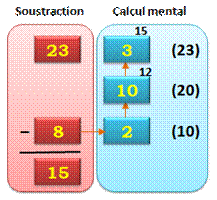
10 = 1 + 9 = 2 + 8 = …	Compléments à 10, utilisés notamment pour le calcul mental. Exemple de calcul avec complément à 10
10 + 9 + 8 + … + 2 + 1 = 10 x 11 / 2 = 55	La somme des entiers jusqu'à 10 est un repdigit. Le plus petit exemple parmi trois connus.
n_n = 10 = 2₂ = 3₃ = … = 10₁₀ = … n_n² = 100 = 4₂ = 9₃ = … = 100₁₀ = …			Le nombre n exprimé dans la base n s'écrit toujours 10. Son carré vaut 100.

Addition

Diagramme de Ferrers du nombre 10

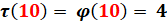
Voir Diagramme de Ferrers

10 = 5 + 5 = 4 + 6 = 3 + 7 = 2 + 8 = …		42 partitions de 10.
p(10) = 42 – toutes 4 – en carrés 2 – en cubes 1 – en puissances 10 – distinctes		Quantité de partitions du nombre 10.
10 = 1 + 2 + 3 + 4		Partition unique avec quatre chiffres différents. Somme des quatre premiers nombres.
10 = 5 + 5 et 5 x 5 = 25		La bipartition qui donne el plus grand produit.
10 = 1 + 2 + 3 + 4 = 5 x 2 10 = 1 + 3 + 6 10 = 2 + 3 + 5		Somme des quatre premiers entiers. Somme égale au double du nombre suivant. Nombre à la fois triangulaire (4^e) et triangulaire centré (3^e). Plus petit deux fois polygonal. Nombre tétraédrique. Somme des trois premiers nombres premiers.
10 = T₁ + T₂ + T₃ = 1 + 3 + 6 = ½ (3n² + 3n + 2) avec n = 2		Somme de trois nombres triangulaires.
10 = 0! + 1! + 2! + 3!		Somme des quatre premières factorielles.
10 = 3 + 7 = 2 + 3 + 5		Somme des nombres premiers jusqu'à 5. Plus petit nombre somme de deux et trois nombres premiers distincts. Tableau des cinq partitions de 10 en nombres premiers.
10 = 2 + 3 + 5 10 = 2 × 5		Somme de premiers consécutifs, produit des extrêmes de la somme. Liste de tels nombres: 10, 39, 155, 371, 2935561623745, 454539357304421 OEIS A055233 Voir premiers consécutifs
10 = 1 + 1 + 1 + 2 + 5 = 1 x 1 x 1 x 2 x 5		Motif avec somme et produit.
10 = (1) + (1+2) + (1+2+3) = 3x1 + 2x2 +1x3		Somme des trois premiers triangulaires.
10 = 3 + 7 = 2 + 3 + 5 = 5 + 5		Plus petit nombre présentant une double partition en premiers distincts. Plus petit aussi pour une double partition en deux nombres premiers.
10 = 3 + 7 = 5 + 5		Plus petit nombre deux fois somme de deux nombres premiers.
10 = 2 + 3 + 5 10² = 2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23		Partition unique avec trois premiers. Somme des trois premiers nombres premiers consécutifs. Son carré est somme des neufs premiers.
10 = 2 × 5 = 2 + 3 + 5	Nombre (composé) égal à la somme des premiers entre le plus petit facteur et le plus grand. Ils sont quatre inférieurs à 10¹²: 10, 39, 155, et 371. Le suivant: 2 935 561 623 745.

Multiplication & division

Table de multiplication du 10

Voir Table complète

10 = 2 x 5	Nombre composé. Nombre simple. Nombre semi-premier. Le seul dont la somme des diviseurs (2 + 5 = 7) et la différence (5 – 2 = 3) sont deux nombres premiers.
10 = 2 + 3 + 5	Somme des premiers compris entre ses facteurs extrêmes (2 et 5).
	Les nombres entiers divisés par 10 produisent ces décimales uniques. Tous les chiffres en séquence.
Somme des diviseurs propres = 8	Le plus petit nombre déficient terminé par 0.
10 = tau (48)	Quantité de diviseurs de 48.
	Un des sept nombres ayant cette propriété: la quantité de diviseurs est égale à la quantité de nombres premiers avec lui et inférieurs à lui (totient).
	Malgré des recherches jusqu'à 10³⁰, on ne sait pas si le nombre 10 est solitaire. On se sait pas si un autre nombre à le même taux d'abondance, rapport de la somme des diviseurs au nombre.
10ⁿ	Voir Premiers voisins de 10ⁿ.

Puissances

10 = 1² + 3²	Seule somme de carrés >>>
	Tout nombre pair est la différence de carrés de deux nombres successifs moins 1, le plus petit étant la moitié du nombre initial.
10 – 1 = 9 = 3² 10/2 – 1 = 4 = 2²	Nombre et sa moitié produisant des carrés.
10 = 2¹ + 2³ = 3⁰ + 3² = 9⁰ + 9¹	Nombre décomposable sommes de puissances dont une en puissances successives.
10 = 1¹ + 2¹ + 3¹ + 4¹ = 2 x 5	Somme de puissance de nombres consécutifs, divisible par le nombre suivant. Propriété générale .
1² + 3² = 1² + 1² + 2² + 2² 10 = 10x1² = 1x2² + 6x1² = 2x2² + 2x1² = 1x3² + 1x1²	2 fois somme de n carrés, n 5. Il existe 4 partitions de 10 en sommes de carrés.
10 = 1² + 3² = (1² + 1²) (1² + 2²) = 2² + 2² + 1² + 1²	Somme de carrés, produit de somme de carrés. Nombre de Brahmagupta.
10 = 4² – 3² + 2² – 1²	Motif dont toutes les puissances paires sont divisibles par 5.
10 = 1³ + 1³ + 2³	Une fois somme de n cubes, n 5
10 = 2 x 5 1² + 3² = (1² + 1²) x (1² + 2²)	À la fois: somme de 2 carrés et produit de deux nombre eux-mêmes somme de 2 carrés. Comme: 4 10 16 20 25 26 34 36 40 50 … Identité de Lagrange
10 = 1³ + 1³ + 2³ = (–3)³ + (–3)³ + (4)³ = 64 – 27 – 27 = 130³ + 141³ + (–171)³ = (–353)³ + (–650)³+ 683³ = …	Partition du nombre 10 en sommes de cubes.
10 = 13³ – 3⁷ = 2 197 – 2 187	Différence entre puissances (seule différence égale à 10 jusqu'à un million et sans doute au-delà).
1 + 2 + 3 + … + 10 = 1² + 2² + 3² + 4² + 5²	La somme des nombres de 1 à 10 est égale à la somme de carrés consécutifs. Seuls cas: (1, 1), (10, 5), (13, 6) et (645, 85).

En puissances

Puissances

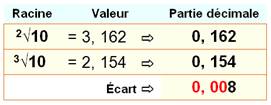
Voir Puissance de 10 / Racine

10² = 2 x 7² + 2	Objet d'un triangle entier.
10² = 6² + 8² = 26² – 24²	Deux triplets de Pythagore.
10² + 11² + 12² = 13² + 14²	Unique telle sommes de carrés de nombres consécutifs.
10³ = 10² + 30² = 18² + 26²	Cube somme de deux carrés.
10² – 1 = 99 = 9 x 11 10³ – 1 = 999 = 9 x 111	Les puissances de 10, moins 1, sont divisibles par 9, et par 99 pour les puissances impaires.
10¹⁰ (10¹⁰)¹⁰ < 10^{(10^10)}	Dix milliards . Puissances de 10 à étages.
	Nombre dont la partie décimale des racines carrée et cubique sont voisines. Voir Liste de tels nombres / Nombre presque entier / Nombres à motifs
10³³ = 8 589 934 592 × 116 415 321 826 934 814 453 125	La plus grande puissance de 10 dont les deux facteurs s'écrivent sans "0".
10		Formule sur le modèle Bombelli.

Factorielles …

10! = 6! x 7! = 3 628 800

10! = 1! x 3! x 5! x 7!

Seule factorielle telle que n! = a! (a+1)!

Produit de deux factorielles consécutives.

Produit de quatre factorielles en progression arithmétique.

10! = 6 × 7 × 24 × 3600

Exactement égal à six semaines comptée en secondes

F₁₀ = 55 et 5 + 5 = 10

La somme des chiffres du 10^e nombre de Fibonacci est égale à 10.

Autour du nombre

10 est divisible par 1 + 0		Nombre de Harshad (trivial).
10 => {3, 7, 9}		Nombre dont les copremiers sont tous sans facteurs simples. Le dernier est 60.
10 = 1 + 2 + 3 + 4 = ½ (3 x 2² + 3 x 2 + 2)		Triangulaire centré.
10 = 3 x 4 x 5 / 6		Nombre pyramide triangle.
10 = 1 + 3 + 6 = (3 x 4 x 5) / 6		Nombre tétraédrique (3^e). Somme des premiers nombres triangulaires). Un des cinq nombres à la fois triangulaire et tétraédrique.
10 = C₅² = C₅³		Nombre du triangle de Pascal. Combinaisons de 5 objets pris 2 par 2 ou 3 par 13.
10 = 4 x 2² – 3 x 2		Décagonal.
10 = 2 x 5		Nombre équidigital. (même quantité de chiffres pour écrire les diviseurs), le plus petit (hors nombres premiers).
10	Le plus petit nombre anticoïndicateur.
10	Quantité de possibilités de classer les chiffres de 1 à 5 en deux ensembles dont chacun contient au moins deux chiffres. Quantité de façons de repartir 5 balles dans deux paniers avec deux balles minimum dans chaque panier.

10 nombres premiers		En progression arithmétique. Record. Voir 10⁹³
10 = 2⁵ / 5 + 2³ / 3 + 14 / 15 = 6,4 + 2,666 + 0,9333		Entier curieux en puissance de 5, 3 et 1.
10 = (5 + -15) + (5 – -15) = (5 + -15) (5 – -15) / 4		Problème de Cardan et découverte des nombres imaginaires : divisez 10 en 2 parties telles que leur produit donne 40 (Intérêt historique uniquement).
10 = 3² + 3/3		Faire 10 avec k chiffres identiques.
			Exemple résistance équivalente.
10^è problème de Hilbert		Il n’y a pas d’algorithme indiquant si une équation diophantienne possède *ou non* une solution >>>
	Le nombre de classe de ce corps quadratique est 2. Ce corps contient tous les nombres de la forme a + ib avec a et b rationnels. Il existe 18 tels corps avec k = 5, 6, 10, 13, 15, 22, 35, 37, 51, 58, 91, 115, 123, 187, 235, 267, 403, 427. OEIS A005847 / Table

Σ λ(10) = 0

Somme de la fonction de Liouville, nulle pour 2, 4, 6, 10, 16, 26, 40, 96, 586, 906 150 256, …

Arithmétique à niveau d'index symétrique

Symmetric level index arithmetic (SLIA); alternative to floating point ?

10 est représenté par 0,834032445247958…

10¹⁰⁰ (google) sera représenté par 4,5268756157751…

0,8340 … est le "level-index" de 10.
Nombre à k étages d'exponentielles (power tower) avec pour dernier exposant un nombre entre 0 et 1.

Représentation des très grands nombres facilitant le calcul sur ordinateurs car ne produisant pas de dépassement de capacité (overflow).

Capable de représenter des nombres dont l'exposant est lui-même très grand, ce que ne permet pas le format flottant (floating point).

Voir Arithmétique – Définition

Voir Symmetric level-index arithmetic – Wikipedia

Jeux et dénombrement

Faire 10 avec k fois le chiffre 9

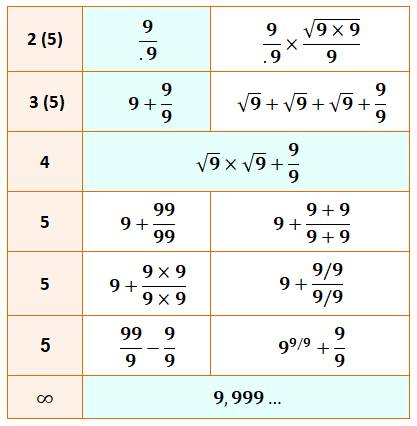
Voir Faire 100 en chiffres et autres défis de ce genre / Brève 921

Jeu du quatre 4.

Coefficient du binôme ou nombre de Pascal. Quantité de combinaisons de 2 parmi 5.

Dimension 2 : 10 types de variétés

Dimension 3 : 105

Dimension 4 : plusieurs millions

Le mathématicien Gino Fano, en 1930, commence à étudier les variétés, à les classer. Il s'agit de variétés que l'on peut visualiser en considérant qu'elles ont une courbure positive et sont donc analogues en dimension supérieure de la sphère.

Une variété de Fano est une variété algébrique projective lisse connexe, définie sur

un corps algébriquement clos, dont le fibré anticanonique (c’est-à-dire le déterminant

du fibré tangent) est ample. – Olivier Debarre

En décimales

	Nombre métallique d'ordre 10.
10, 392 304 85… = 63	Aire de l'hexagone de périmètre 12.
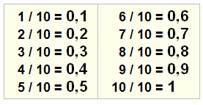
	Racines carrées de factorielles.
1 / 10,89 = 0,09 18 27 …	Suite des multiples de 9.

Suite Géométrie, Jeux, Culture …

Devinette – Solution

Avec une seule barre rétablir l'égalité:

On est vite amené à penser arithmétique avec 10 et 11 et la moyenne 10,5; le point tenant lieu de virgule chez les Anglo-Saxons.

Puis vient l'idée du codage en binaire 10 10 11₂ = 43₁₀. En cherchant bien on trouve: 1010.1 / 1 = 10,5 qui répond à la question mais avec un point en plus de la barre. Pas loin! On s'acharne …

En fait, la solution n'est pas mathématique. C'est l'expression d'une heure en anglais qui se lit "ten to eleven equal ten fifty" (onze heures moins dix égal dix heures cinquante.