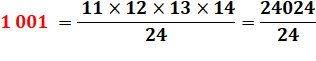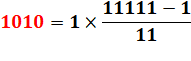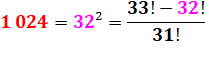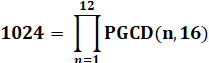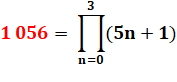NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/09/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres		DicoNombre NOMBRES						Glossaire Nombres
1 10 100 / 200 300 / 400 500 / 600 700 / 800 900 / 1 000		1 001 à 1 099						1 100 / 1 200 1 300 / 1 400 1500 / 1900 2000 / 3000 10 000 100 000 10^6 / 10^9 / 10^100
		Mille un à mille quatre-vingt-dix-neuf Anglais: One thousand and one
1 000	1 001		1 010	1 020	1 050	1 080	1 090		1 100
				1 024		1 089

1 001

1 001 = 7 × 11 × 13 = 11 × 91		Facteurs: trois nombres premiers consécutifs. Explique que les records de quantité de diviseurs de nombres avec chiffres répétés comme: 720720, 1081080, 1441440, 2162160, 2882880, 3603600, … Liste des nombres à trois facteurs premiers consécutifs: 30, 105, 385, 1001, 2431, 4199, 7429, 12673, 20677, 33263, 47027, 65231, 82861, 107113, 146969, 190747, 241133, 290177, 347261, 409457, 478661, 583573, 716539, 871933, … OEIS A046301
1 001^7 = 10070210350 35021007001		Mêmes chiffres dans chacune des moitiés de ce carré. Voir Nombre 207 (table)
			Le produit de quatre nombres consécutifs est divisible par 24. Tous ces nombres figurent dans la cinquième diagonale du triangle de Pascal.
1 001 = 1 + 4 + 10 + 20 + 35 + 56 + 84 + 120 + 165 + 220 + 286			Somme des onze plus petits nombres tétraédriques.
				Nombre glissant. 1010 et 1100 sont aussi des nombres glissants.
1 001	Tous les nombres de la forme AA, avec A à trois chiffres (a, b et c), sont divisibles par 1001 et ses diviseurs. Objet de multiplications magiques.
1001 | 10^1001+1 – 1	Cas de divisibilité aussi observé pour: 3, 9, 11, 33, 77, 99, 143, 303, 369, 407, 707, 959, 1001, …

Factorisation particulière des nombres en 10^k + 1

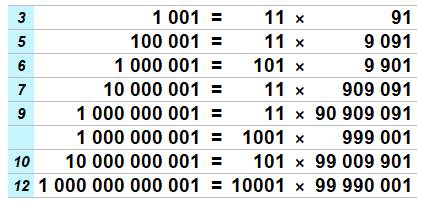
Voir Nombre 1 000 000 001

Jeux

1 001 = 77 x ( 7 + 7 – 1 )

>>>

Suite en Page spéciale nombre 1 001

1 002

1 002

Quantité de partitions de 22.

Littérature	1 003 femmes auraient été séduites par Don Juan. Devenu une expression en Espagne: il y 1 003 façons d'étudier le problème	>>>
Langue	1005 = one thousand and five Plus petit nombre en anglais avec les cinq voyelles.	>>>
Sciences	1 015 hPa pression-limite entre dépression et anticyclone.	>>>

1 003 = 17 × 59	Nombre brillant: deux facteurs de même taille. Le plus petit à quatre chiffres.
1 007 = 9 + 99 + 999	Somme des nombres en 9.
1 007 => {7, 17, 71, 107, 701, 7001} sont premiers	Nombre composé multi-premier.

Humour

Combien ça fait si tu additionnes 3 et 5, Émile ?

- Facile, 1008 !

Voir Pensées et Humour / Prénoms amusants

1 008 = 12 × 84 = 21 × 48		Abondant (hautement -) Double forme retournée.
1 008 = 2^3 + 10^3		Nombre binomial.
1 008 =		Quantité de possibilités de lire Mississippi dans une grille 13x13 de mots carrés.
1 008 / 168 = 6		Il y a 168 nombres premiers jusqu'à 1008. Exactement un nombre sur six. Même proportion pour 1080, 1092, 1116, 1122, 1128 et 1134.
		Nombre égal à six fois la quantité de premiers qui lui sont inférieurs. Le plus petit cas. Liste des nombres : 1008, 1080, 1092, 1116, 1122, 1128, 1134.
1 009		Le plus petit nombre premier à quatre chiffres. Premier bon. Premier de Ramanujan.
1 009 = 10^3 + 2^3 + 1^3 = 9^3 + 6^3 + 4^3		Deux fois somme de trois cubes distincts. Plus petit cas.
1 009 = 15² + 1x28² = 19² + 2×18² = 31² + 3×4² = 15² + 4×14² = 17² + 5×12²	= 25² + 6×8² = 1² + 7×12² = 19² + 8×9² = 28² + 9×5² = 3² + 10×10²		Nombre multi-somme de type A² + kB². Record, après 241, avec les dix représentations jusqu'à k = 10.

1 010

10102 = 1010	Binaire et équivalent décimal. Curiosité.
	Forme donnant a0a0 en remplaçant 1 par n'importe quel chiffre a.
1 010 = 10 + 10^3	Membre de la suite: an+1 = an + an^3 1, 2, 10, 1010, 1030302010, 1093688489093570254240903010 …
1 010² + 101² = 101^3	Carré + carré du retourné = cube. Explication 1010² + 101² = (101 x 10)² + 101² = 101² x (100 + 1) = 101^3
1 012 = 2 (22 × 23) 4 T22 = CC2 – 1 = 22² + 23² – 1 45² + 1012² = 1013² 990² + 991² + … + 1012² = 1013² + 1014² + … + 1034²	Nombre quadrillage: 1 012 traits dans une grille 22x22. Quatre fois un nombre triangulaire. Nombre carré centré moins 1. Somme de deux carrés moins 1. Nombre central d'un triplet de Pythagore jumeau. Nombre central de cette somme de carrés. Ensemble, ces propriétés sont communes à toute une série de nombres: 4, 12, 24, 40 …
3, 11, 13, 31, 101, 103, 113, 131, 311, 1013, 1031, 1103, 1301, 3011 sont premiers			Nombre multi-premier 14 fois.
1 013, 1 031 et 1301 1031 – 1013 = 18 = 2 x 9 1301 – 1031 = 72 = 8 x 9	Trois nombres premiers dont la somme des chiffres est 5. La différence entre eux est un multiple de 9. Ces trois premiers semblables se succèdent dans la liste de somme 5.
1 013	Primeval. Nombre carré centré.
1015, 1015, 1016, 1017	Quatre nombres de Harshad successifs. Évidemment divisibles par des nombres successifs, somme des chiffres des nombres. Première occurrence. Suivante: 2022, 2023, 2024, 2025.
1 015 = 1² + 2² + … + 14²	Pyramidal carré. Le plus petit des nombres pyramidaux jusqu'à base octogonale Somme de carrés de nombres consécutifs.
1 016	Inconsommable, le plus petit à quatre chiffres.
1 019	Premier bon
		Égalité pour deux nombres voisins du produit du totient et de la somme des diviseurs.
1 015^3 = 1 045 678 375	Curiosité: plus petit cube ayant cinq chiffres successifs.
1 016	Nombre refactorisable. Nombre de Mian-Chowla.

1 020

1020 est divisible par 4 102 est divisible par 3 10 est divisible par 2 1 est divisible par 1			Nombre polydivisible: le plus petit à quatre chiffres.
102110 = 1 111 111 1012 = MXXIR			Voir le nombre décimal 1 111 111 101 et ses propriétés.
1 022 = 2^10 – 2			Mêmes chiffres de part et d'autre de l'égalité.
1 022² = 197² + 198² +…+ 220² = 1 044 484			Somme de carrés consécutifs égale à un carré.
1023	Plus petit nombre à quatre chiffres dont les chiffres sont distincts. Le plus grand étant 9876.
1 023 = 2^10 - 1 = 512 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 1 1 1 1 1 1 1 1 1 1en binaire			Somme des puissances successives de 2
1 023 = 11 x 93		Plus petit nombre à quatre chiffres différents divisible par 11. Le plus petit sans le 0 est: 1 243.
1 023! = (1 023 – 10)^2 × K		Toutes les factorielles sont divisibles par des puissances de 2 de plus en plus grandes. 1 023 est le nombre tel que sa factorielle a pour facteur 2^1013, un exposant qui atteint pour la première fois un écart de 10 avec le nombre-factorielle.

1 024

1 024 = 32²	Plus petit carré avec seulement quatre chiffres différents. 12 769 = 113² est le suivant avec cinq chiffres.
	Carré = cette relation entre factorielles successives.
1 024 = 4^10 / 5	Anagrammes numériques. Nombre de Friedman. Frugal
1 024 = 2^10 = 4^5 = 32^2 = 2^9 + 2^9 = 4 × 4^4 = 2 × 8^3 = 2^5 × 2^5 = Mnémotechnique: 2^10 = 10 24	Puissance cinquième de 4. Nombre n (= 4) à la puissance n+1. Abréviation " kilo " en Informatique car proche de 1 000. Exemples : 1 kilobit = 1024 bits 1 kilooctet (ou kilobyte en anglais) = 1024 octets (mot de 8 bits). Voir Méga / deux puissance dix
2^10= 1024 2^20= 1048576 2^30= 1073741824 2^40= 1099511627776 2^196= 100433… 2^392= 100869… 2^681= 100329… 2^877= 100764… … 2^2136 = 1000162…	Puissances de 2 commençants par 10, par 100 ou par 1000. Avec 3^k, ces puissances commencent par 10 pour: 21, 42, 65, 86, 109, 130, 174, 195, … Avec 4^k, ces puissances commencent par 10 pour: 5, 10, 15, 20, 98, 103, 108, 113, 196, … et même 100 pour 98 et 196.
1 024 = 4 × 4^4	Somme de la puissance 4 des chiffres du repdigit 4444 à quatre chiffres. Nombre ABA (A·B^A).
	Puissances avec les mêmes chiffres. Les deux seules puissances pures avec les chiffres de 1024, hors 4 = 2².
1 024 = 40² – 24² = 32² = 8² x 4² 1 024 = 130² – 126² = 32² = 16² x 2²	Nombre complètement carré.
1 024 = 32^2 2 401 = 49^2	Motif avec permutation des chiffres.
1 024	2 à 10 – rond
–1024 = (4 + 4i)^4 = (4 – 4i)^4 = (2 + i2)^12 = (2 – i2)	Entier = puissance de nombre complexe. Voir Pépites
–1024 = (1 + i)^19 + (1 – i)^19	Complexe et puissance de 2.
	Le produit des PGCD des nombres de 1 à 12 avec 16 vaut 1024. Ce qui reste vrai jusqu'à 13. Formulation Voir Nombre 800 / Nombre 2025

1 025

1 025 = 1² + 32² = 1 + 1 024 = 8² + 31² = 64 + 961 = 20² + 25² = 400 + 625	Multi somme de carrés.
		Quatre fois somme d'un cube et d'un carré. Plus petit tel motif.

1 027 = 27 + 28 + … + 52	Nombre 2-pentagonal: somme des vingt-six nombres supérieurs à 26.
1 027 = 2^2 + 3^2 + 5^2 + 7^2 + 11^2 + 13^2 + 17^2 + 19^2	Somme des carrés de huit premiers consécutifs.
1 027 = 10^3 + 3^3 = 1000 + 27 = 19^3 – 18^3 = 6859 - 5832	Nombre binomial. Deux fois somme de deux cubes avec nombres négatifs autorisés. Voir Table
		Le repunit formé de 1031fois le chiffre 1 est premier. Ils sont cinq connus.

1 030

1031, 1033, 1301, 1303

Paires de jumeaux permutées.

1 033 = 8^1 + 8^0 + 8^3 + 8^3 12 = 3^1 + 3^2 4 624 = 4^6 + 4^6 + 4^2 + 4^4 etc.	Motifs avec les chiffres en puissance d'un même nombre.
1 034 = 1^1 + 0^1 + 3^2 + 4^5		Nombre élégant: somme de ses chiffres en puissance. Plus petit à quatre chiffres.
1 035 × 3 = 3 105 10 035 × 3 = 30 105 100 035 × 3 = 300 105 … 10 350 = 3 × 31 050 …		Mêmes chiffres pour son triple (le plus petit de deux à quatre chiffres; l'autre: 2 474) Cette propriété est conservée en ajoutant des 0.
1 036		Nombre tarte.
1 036^3 = 1 111 934 656		Plus petit cube commençant par quatre chiffres identiques. Liste: 1036, 1305, 2232, 4808, 6057, 6934, 9615, … Voir Nombre 322 / Nombre 9 615
1 037 = 17 x 61		Primeval.
1 037 => 3, 7, 13, 17, 31, 37, 71, 73, 103, 107, 137, 173, 307, 317, 701, 1307, 3701, 7013, 7103 sont premiers			Nombre composé multi-premier 19 fois.
1 037 = 6^4 – 6^3 – 6^2 – 6^1 + 6^0				Suite de puissances de 6.
1 039 => 3, 13, 19, 31, 103, 109, 139, 193, 1039, 1093, 3019, 3109, 9013, 9103 sont premiers				Nombre multi-premier.

Littérature

1 039 romans du romancier brésilien Brazil-Ryoki Inone. Il est le recordman de production de romans avec 1 039 livres. Il admet : " Franchement, je n'ai pas lu tous les livres que j'ai écrits ".

>>>

1 040

1 040 = 2^4 × 5 × 13 1 230 = 2 × 3 × 5 × 41 1 640 = 2^3 × 5 × 41		Plus petit nombre dont la factorisation contient les quatre premiers chiffres. Les deux suivants.
1 040, 1 044, 1 048		Trois nombres refactorisables.
1 040 = 6^4 – 4^4		Nombre binomial.
1 041		Entier de Blum (facteurs = 3 mod 4)
1 042 => 1^3 = 1, 0^3 = 0, 4^3 = 64, 2^3 = 8 => 10648 = 22^3				Nombre dont les chiffres mis au cube puis concaténés produit un cube.
1 042 => (1 + 0 + 4 + 2)^4 = 2 401			La puissance 4 de la somme de ses chiffres est son retourné. Seul cas avec la puissance 4. Voir Nombre 215 pour le cube
1 044			Quantité de graphes simples à sept sommets.
1 045		Nombre octogonal (19^e).
1 049 => 19, 41, 109, 149, 401, 409, 419, 491, 941, 1049, 1409, 4019, 4091, 9041 sont premiers					Nombre multi-premier.
1 049² = 1100401	Nombre et son carré formés de chiffres carrés. Rare.

1 050

1 050	Faiblement totient
			Nombres Fiancés
1 051		Nombre pentagonal centré.
1 051 & 1 061 10 501 = 3 491 + 3 499 + 3 511 10 601 = 3 529 + 3 533 + 3 539 1 051 + 1 061 = 2112 1 051 x 1 061 = 1115111 1 051 ^2 + 1 061 ^2 = 2230322		2 premiers consécutifs Palindromes, somme de 3 premiers consécutifs. Palindromes
1 053 / (1+0+5+3) = 117 1 053 / (1+0+5+3)² = 13		Harshad avec chiffres distincts: divisible par la somme de ses chiffres et aussi divisible par le carré de cette somme.
1 054		Nombre triangulaire centré.
1 056 = 2^5 + 4^5		Nombre binomial.
		Factorielle quintuple de 3 = (5x0+1) (5x1+1) (5x2+1) (5x3+1) = 1 x 6 x 11 x 16
1 05710 = 1 0000 1 0000 12		Palindrome en binaire.
1 060 = 2 + 3 + 5 + … + 97		Somme de 25 premiers nombres premiers. Somme de tous les nombres premiers inférieurs à 100.
1 061		Premier irrégulier. Quantité de nombres premiers à quatre chiffres.
2^1061 – 1		Factorisation découverte en 2012. Cunningham Project.
1 064 = 4^3 + 10^3		Nombre binomial.
1 068		Qpart(15). Quantité de sommants de toutes les partitions du nombre 15.

1 070

1 071 = 6^3 + 7^3 + 8^3 = 21 x 51	Somme des cubes de trois nombres consécutifs, toujours divisible par trois fois celui du centre.
1 072 = 2^3 + 4^3+ 10^3 = 7^3 + 9^3 1 800 = 2^3 + 4^3+ 6^3 + 8^3 + 10^3 = 6^3 + 7^3 + 8^3 + 9^3		Nombre binomial. Somme de cubes Résulte de cette égalité entre pairs et successifs au cube.
1 079 => 7, 17, 19, 71, 79, 97, 107, 109, 179, 197, 701, 709, 719, 907, 971, 1097, 1709, 1907, 7019, 7109, 7901 sont premiers			Nombre multi-premier Primeval.
1 079 = 7² + 13² + 31² = 7² + 17² + 29² = 11² + 23² + 23² = 13² + 13² + 29² = 17² + 19² + 23²	Cinq fois somme de trois nombres premiers au carré. Plus petite cas.

Géométrie	1080° = 6 x 180° Somme des angles de l'octogone.	>>>
Multimédia	TV HD 1080p Standard européen de la télévision haute définition.	>>>

1 080

1 080	Nombre pentagonal.
1 080: Somme diviseurs = 3 600 Produit des facteurs = 2x3x5 = 30 S / P² = 4	Nombre tel que la somme des diviseurs est divisible par le produit des facteurs au carré.
Div(1080) = {1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 27, 30, 36, 40, 45, 54, 60, 72, 90, 108, 120, 135, 180, 216, 270, 360, 540, 1080}		Ce nombre compte 32 diviseurs.
1 082	Nombre tarte.
1 087	Premier de Kynea.
1 088 = 2^6 × 17 & 1+0+8+8 = 17	Nombre dont le plus grand facteur est égal à la somme de ses chiffres.

1 089

Voir Page spéciale sur le nombre 1 089 / Carrés magiques avec 1 089 / Tour de magie avec 1 089

1 090

1 092 = 3^1 + 3^2 + 3^3 + 3^4 + 3^5 + 3^6	Somme de puissances de 3.
1.2² + 2.3² + 3.4² + 4.5² + 5.6² + 6.7² + 7.8²	Somme de produits de nombres consécutifs.

364 = 111 1113 1 093 = 1 111 1113 3 280 = 11 111 1113	Repunit en base 3.
1 093 = 1 093 1 facteur 1 094 = 2 x 547 2 facteurs 1 095 = 3 x 5 x 73 3 facteurs 1 096 = 2^3 x 137 4 facteurs	Quatre nombres consécutifs dont la quantité de facteurs va croissant de 1 à 4.
1 093	Panconsommable Toujours atteint par k / (somme des chiffres de k) dans toutes les bases.
1 093 | (2^1093-1 – 1) 3 511 | (2^1093-1 – 1)	Deux seuls premiers connus de Wieferich.
1 093 2^1 093 – 1 – 1 divisible par 1 093² 2^3 511 – 1 – 1 divisible par 3 511² 2^p – 1 – 1 divisible par p²	Nombre étoilé. Seuls ces 2 nombres ont cette propriété jusqu'à 10^10, au moins. Voir Wieferich / Paires de Wieferich / Fermat

1095 – 1270	Les croisades Mnémotechnique: TSPL et TNKS qui devient: Avec Ton SPLeen, Tu Nous les CaSSes.
1 097	Rang d'un nombre de Lucas premier.
[1097, 1709, 1907, 7019, 7109, 7901]	Ces six nombres sont premiers et ont exactement les mêmes chiffres.
	Le plus petit nombre tel que son totient (phi) atteint 2 après dix itérations.
1 096	Nombre Hendécagonal.
1 099	Table de multiplication du nombre 1099: saut d'une unité en plus ou en moins pour les unités, les centaines et les milliers. Principe valable pour de nombreux nombres en 111… – …11 comme 109

Suite	Nombres 1 100
Voir	Nombre Chanceux Semaine Palindrome Triangle Tectroèdre Raisonnement Rep Unit Suites Nombre Têtus
Site	Références Internet
Cette Page	http://villemin.gerard.free.fr/NombDico/N1000/N1001.htm

Quelques repères dans ces pages >>> NOMBRE 1 001 Palindrome >>> NOMBRE 1 024 Puissance de 2 >>> NOMBRE 1 025 Somme de carrés >>> NOMBRE 1 051 et Nb 1061 >>> NOMBRE 1 089 Retournement >>> NOMBRE 1 093 Fermat

>>> MAGIE >>> MULTIPLICATION MAGIQUE >>> SHÉHÉRAZADE >>> DON JUAN