NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/06/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Forme des nombres
Débutants Nombres figurés	NOMBRES FIGURÉS			Glossaire Nombres figurés
INDEX Nombres géométriques Géométrie Nombres	Introduction	Théorie (propriétés)	Calcul	Tables
		TYPES (triangle, carré, pentagonal …)
		Sommaire de cette page >>> Construction des nombres polygonaux de 3 à 8 >>> Extension >>> Types de nombres figurés >>> Un peu de théorie >>> Formule générale d'un nombre polygonal

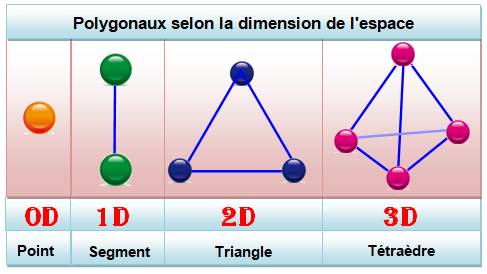
NOMBRES FIGURÉS,

Géométriques ou Polygonaux

Nombres qui peuvent être représentés par des figures géométriques. Ils recèlent une quantité phénoménale de propriétés. Amusantes, et en général simples. Ils ont passionné les Grecs au temps de Pythagore. Diophante y a consacré un tome de son œuvre, Les Arithmétiques.

Théorème fondamental des nombres figurés

Tout nombre entier est une somme de (au plus) :

3 nombres triangulaires

4 nombres carrés

5 nombres pentagonaux

etc.

Voir Partition / Somme de 4 carrés

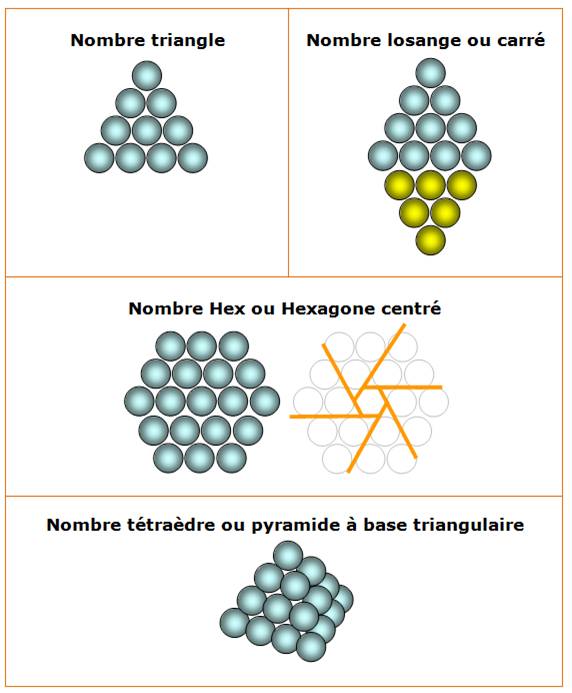
Nombres spécifiques

10	Nombre sacré
100	Phénomène géométrique
40 755	Triangulaire Pentagonal Hexagonal

Voir Nombres à motifs

CONSTRUCTION des NOMBRES FIGURÉS ou POLYGONAUX avec 3 à 8 côtés

Voir Chacun de ces types et les autres

Extension des NOMBRES POLYGONAUX - Exemples

Types

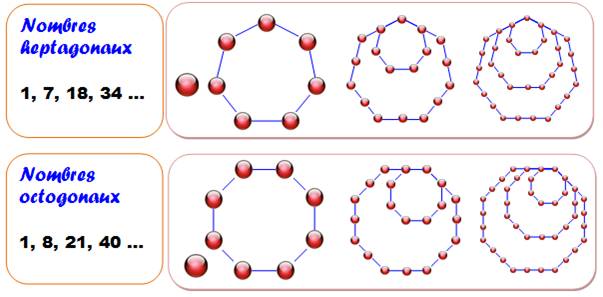
Nombres figurés ou géométriques

Nombres polygonaux pour la dimension 2 (plan),

Nombres polyédraux pour la dimension 3 (espace), et

Nombres figurés généralisés pour les dimensions 4 et plus.

Voir Types de nombres figurés: liste et liens

UN PEU DE THÉORIE
Nombres polygonaux ou figurés Ils sont représentés par une quantité de points sur une figure géométrique régulière. La suite de ces nombres est construite à partir d'une progression arithmétique.
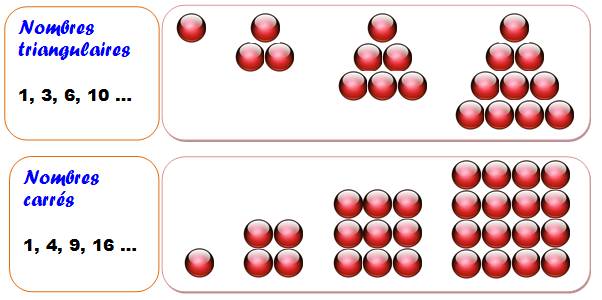
Triangulaire Progression arithmétique Construction	1, 3, 6, 10 … 1, 2, 3, 4 … (de raison 1) 1 = 1 3 = 1 + 2 6 = 1 + 2 + 3 10 = 1 + 2 + 3 + 4
Carrés Progression arithmétique Construction	1, 4, 9, 16… 1, 3, 5, 7… (de raison 2) 1 = 1 4 = 1 + 3 9 = 1 + 3 + 5 16 = 1 + 3 + 5 + 7
Formulation générale Progression arithmétique Raison Polygone – Quantité de côtés	Xn = 1 + a2 + a3 + … + an 1, a2, a3… r = p – 2 p = 1 + a2
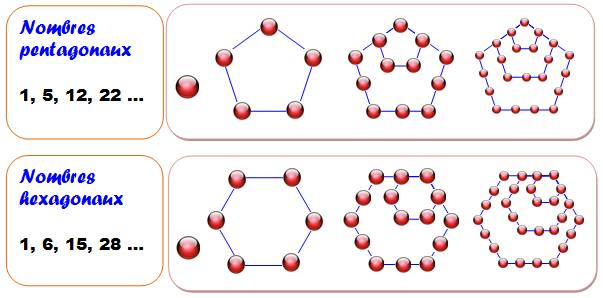
Hexagonaux (exemple) Polygone – Quantité de côtés Raison Progression arithmétique Nombres hexagonaux	p = 6 = 1 + 5 r = 6 – 2 = 4 1, 5, 9, 13… 1, 6, 15, 28…

Voir Suite sur les propriétés des nombres polygonaux

Suite	Formules de calcul des nombres géométriques Les nombres géométriques en détail, un par un Introduction aux nombres géométriques Théorie des nombres géométriques
Voir	Calcul mental – Index Géométrie – Index Liste des noms des nombres Partition Somme des cubes des entiers TABLES de nombres Théorie des nombres
Site	Nombres figurés de Récréomath Figurate numbers d'Eric Weisstein Absolument intarissable sur le sujet
Livres	Pour développements complets, voir Conway et Guy " The book of numbers " (Le livre des nombres) Figurate numbers – Elean Deza et Michel Marie Deza – World Scientific – 2012 – Un bible de 469 pages
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbGeomet.htm