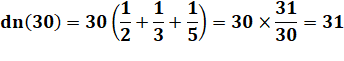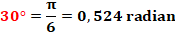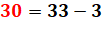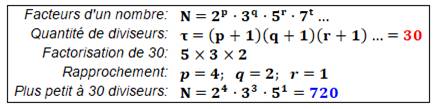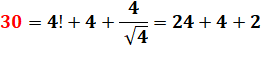Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 22/01/2025 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	30	31		32	33		34	35	36	37	38	39

Nombre 30	Maths générales du 30	Maths détaillées du 30	Histoire 30
		Propriétés géométriques de 30	Expression 30

Trente

Thirty

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1 1110
Bases	506 339 2214
Romain	XXX
Diviseurs	1, 2, 3, 5, 6, 10, 15, 30
	30 = 5 + 10 + 15 (semi-parfait)
Quantité	8 (4 pairs et 4 impairs)

Suite

Mélange romain et décimal

10 fois 10 égal 30

Caractérisation du nombre

3-rond

Abondant,
le précédent est 34

Abondant (hautement -)

Abondant primitif

Admirable

Ami avec 140

Balancé

Composé (n°19)

Composé inévitable (ou minimal)

Congruent

Constructible

Cullen moins

Curzon

Factorielle Fibonacci

Faiblement totient

Générateur de Woodall

Giuga

Harshad ou Niven

Idéal

Idonéal

Interpremier (29, 30, 31)

Narcissique de Keith

Narcissique généralisé

Pair

Partition

Pratique

Primorielle (2×3×5)

Queneau

Régulier ou 5-friable

Semi-parfait

Simple

Sphénique

Zumkeller

Païen (evil) et poney

Pronique

Pyramidal carré (4^e)

Pyramidal octogonale (3^e)

Hendécagonal

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Rappel Propriétés générales >>>

On ne comprend guère le mot jeunesse avant trente ans.

Jean Dutour

Une femme met au moins quarante-cinq ans

pour arriver à la trentaine.

J'aime bien vivre seule. De toute façon, les hommes ne sont jamais vraiment intéressants avant la trentaine.

Scarlett Johansson – Jeune actrice en 2004

Il faut avoir trente ans pour songer à sa fortune; elle n'est pas faite à cinquante; l'on bâtit dans sa vieillesse, et l'on meurt quand on est aux peintres et aux vitriers.

La Bruyère (1645 - 1696)

Voir Pensées & humour

Caractéristique, forme, numération

30 = 2 × 3 × 5 30 = 2 × 15 30 = 3 × 10 30 = 5 × 6	Nombre composé, le plus petit à trois facteurs distincts. Plus petit avec la signature [1, 1, 1]. Produit des trois premiers nombres premiers. Premier nombre sphénique: produit de trois facteurs seulement (le suivant: 43). Nombre simple et donc sans carré. Primorielle ou produit des premiers nombres premiers. Toutes les primorielles plus grandes sont divisibles par 30.
30 = 3+0 + 3^3+0^3 = 3+0 + 5+9+0+4+9 = 3+0 + 1+2+9+1+4+0+1+6+3		Narcissique de Keith – Triple Somme de ses chiffres et de ceux de son cube; de sa puissance 10; de sa puissance 17. Voir Table des nombres de Keith
30	Nombre binaire en pente (sloping binary number). Le nombre 29 ne l'est pas. De 30 à 61, ils le sont.
30 = 1/3 × 5(5² – 3×5 + 8)		Quantité maximale de régions produites par les intersections de cinq sphères.

Addition et soustraction

			Partitions notables de 30 parmi les 5 604 dont 396 avec des nombres distincts. Certaines sont expliquées ci-dessous.
30 = 2 + 4 + 6 + 8 + 10	Partition particulière de 30: somme des nombres pairs jusqu'à 10.
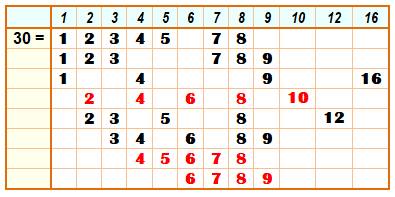
30 = 6 + 7 + 8 + 9 = 4 + 5 + 6 + 7 + 8	Partition unique avec quatre chiffres différents. Somme de cinq nombres successifs. Nombre deux fois poli.
(6 + 7 + 8 + 9 )^10 = 590 490 000 000 000	Grand nombre à "0", avec des nombres consécutifs.
30 = 4 + 5 + 6 + 7 + 8	Une des trois sommes de nombres consécutifs >>>
30 = 6 + 7 + 8 + 9 = (1+5) + (2+5) + (3+5) + (4+5) = 1 + 2 + 3 + 4 + 4x5 = 3 x (1 + 2 + 3 + 4)	Façons amusante d'écrire cette somme.
30 = 6 + 7 + 8 + 9 = 10 x 3 = 9 + 8 + 7 + 6 = 5 x 6 = 8 + 7 + 6 + 5 + 4 = 3 x 10	Somme de consécutifs, égale à un multiple du nombre suivant ou du précédant.
30 = 8 + 10 + 12 = 3 + 3^3	La somme d'une suite de pairs est égale à n + n^3.
30 partitions	Les trente partitions du nombre 9. Le nombre 8 en a 22 et le nombre 10 en a 42.
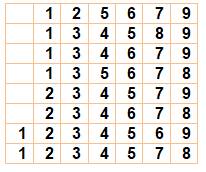
30 = 13 + 17		Somme de premiers consécutifs. Tableau: en tête, 1 et les nombres premiers jusqu'à 30. Notez l'originalité des quatre sommes.
30 = 7 + 23 = 11 + 19 = 13 + 17	Trois fois sommes de deux premiers. Ces nombres sont symétriques par rapport à 15. C'est une règle générale pour toute partition des multiples de 30 en deux nombres premiers.

Multiplication et division

Facteurs(30): 2, 3, 5	Nombre 3-simple de premier rang. Nombre régulier ou 5-friable ou 5-lisse.
28 = 2² × 7 29 30 = 2 × 3 × 5	Plus petit nombre ayant trois facteurs distincts. Liste à trois facteurs: 30, 42, 60, 66, 70, 78, 84, 90, 102, … Liste pour quatre facteurs: 210, 330, 390, 420, 462, … Liste pour cinq facteurs: 2310, 2730, 3570, 3990, … Liste pour six facteurs: 30030, 39270, 43890, 46410, …
30 = 2 × 3 x 5 2 + 3 = 5	Nombre somme-facteurs primitif. Ils sont 12 jusqu'à 10 000.
30 = 2 × 3 × 5 2 + 3 + 5 = 10 = 30 / 3		Nombre divisible par la somme de ses facteurs. Le plus petit. Suivant: 46 206 divisible par la somme des carrés de ses facteurs.
Il y a 10 nombres premiers inférieurs à 30 et, 30 est multiple de 10		Nombre MulQprem.
30 {7, 11, 13, 17, 19, 23, 29}		Plus grand nombre dont tous les premiers avec lui sont premiers.
		Les sommes des carrés des diviseurs sont égales. Seule possibilité (k = 5) pour n + k avec k de 1 à 100.
30 = 1.2.3 + 2.3.4		Somme de produits de nombres consécutifs.
30 = 1 × 1 × 2 × 3 × 5		Produit des cinq premiers nombres de Fibonacci.
30 = 2 × 3 × 5		Nombre de Giuga: la somme des inverses des facteurs diminuée de leur produit vaut 1. Le plus petit.
30 = 5! / 2² = 120 / 4		Factorielle divisée.

29, 30, 31 6n – 1, 6n, 6n +1		Nombre pivot de la barre magique des nombres premiers: 29 et 31 sont premiers jumeaux.
30 = tau (720)		Quantité de diviseurs de 720.
		Le plus grand des sept nombres ayant cette propriété: la quantité de diviseurs est égale à la quantité de nombres premiers avec lui et inférieurs à lui (totient).
		Ces nombres forment un quadruplet d'amis; ils ont le même taux d'abondance.
PGCD(30, 3k+1 < 30) = 1		Les 7 nombres impairs premiers avec 30 sont effectivement premiers.
30 et PPE		Tous les nombres plus petits et premiers avec 30 sont des nombres premiers. 30 est le plus grand nombre ayant cette propriété.
30 diviseurs pour 720 730 = 2^4 x 3^2 x 5	Le nombre 720 est le plus petit ayant 30 diviseurs.
30 x 2^30 – 1 = 0, 322… 10 ^11 = 32 213 254 719 = nombre premier		Générateur de Woodal (4^e).
30 => {7, 11, 13, 17, 19, 23, 29}		Nombre dont les copremiers sont tous sans facteurs simples. Le dernier est 60.
n^5 – n = 30 k		Polynôme divisible par 30 Exemples 2^5 – 2 = 30 3^5 – 3 = 240 = 30 x 8 4^5 – 4 = 1 020 = 30 x 34 5^5 – 5 = 3 120 = 30 x 104 = 240 x 13 (divisible par 240 si nombre impair)
p = 30n + {1, 7, 11, 13, 17, 19, 23, 29}		Tous les nombres premiers peuvent s'exprimer comme multiple de 30 en y ajoutant un des nombres premiers inférieurs à 30, sauf 2, 3 et 5.
2 x 30 – 1 = 59 2 x 30 + 1 = 61		Ces deux nombres sont premiers.

Puissances

	Sorte de moyenne géométrique entre deux premiers jumeaux 29 et 31.
30 et 31	Deux plus grands nombres fluets à deux chiffres.
30 = 0² + 1² + 2² + 3² + 4²	Somme de cinq nombres successifs portés à une puissance. Toutes ces sommes sont divisibles par 5, sauf pour les puissances en multiple de 4.
30 = 1^2 + 2^2 + 3^2 + 4^2 = 5 x 6	Somme de puissance de nombres consécutifs, divisible par les nombres suivants. Propriété Générale .
30 = 1² + 2² + 5² = 1² + 2² + 3² + 4² = 2² + 2² + 2² + 3² + 3² = 1^3 + 1^3 + 1^3 + 3^3	Toutes les sommes de puissances à partir de 2, avec deux à cinq termes.
30 = 3 + 3^3	Nombre narcissique généralisé. Suite n + n^n.
30 = 2^5 – 2^1 = 6^2 – 6^1	Différence de puissances d'un même nombre.
30 = 83^2 – 19^3	Différence entre puissances.
30 = 5^1 + 5^2	Nombre décomposable en puissances successives.
30 = 2^1 + 3^1 + 5^2 = 2^4 + 3^2 + 5^1	Motif trois fois 2^a + 3^b + 5^c.
30 = 4^3 – 2x5^3 + 6^3 = 6 x 5	Expression avec 3 cubes, toujours multiple de 6.
30² = 18² + 24² = 900 = 324 + 576	Triplet de Pythagore. Le seul.
30^2 = 900 => 9 + 0 + 0 = 9 = 3² 30^3 = 27 000 => 2 + 7 + 0 + 0 + 0 = 9 = 3²	Nombre dont la somme des chiffres du carré et celle du cube sont des carrés. Précédent pour le carré: 23² = 529; Suivant pour le carré : 31² = 961.
	Somme de deux cubes rationnels.

Nombre géométrique et géométrie

30 = 4 x 5 x 9 / 6 = 1² + 2² + 3² + 4²	Nombre pyramide Somme de carrés de nombres successifs. Voir Autour de 12345
30 = 1 + 10 + 19	Nombre hendécagonal ou figuré d'ordre 11.
30 = 5 x 6	Nombre Pronique.
Sinus (30°) = ½	Angle du triangle rectangle dont l'hypothèse est double d'un de ses côtés.
30 = aire = périmètre	Du triangle pythagoricien: (5–12–13). Un des deux seuls avec même aire et périmètre.
30 côtés	Triacontagone: polygone à 30 côtés. Constructible à la règle et au compas.
30 arêtes	Icosaèdre et dodécaèdre.
30 polyèdres	Isoèdre: tous les faces sont égales.

Dénombrement, jeux et curiosités

			Avec trois 3.
			Jeu du quatre 4: atteindre 30 avec quatre fois le chiffre 4.
30	Quantité de produits distincts de deux nombres de 1 à 8. Ce sont: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 25, 28, 30, 32, 35, 36, 40, 42, 48, 49, 56, 64
30	Quantité de produits distincts de trois nombres de 1 à 5. Ce sont: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32, 36, 40, 45, 48, 50, 60, 64, 75, 80, 100, 125.
		Rétablir cette addition avec les boules indiquée. Pas si simple … Solution

Autour du nombre

30, 66, 102, 138 2x3x5; 2x3x11; 2x3x17; 2x3x23		Quatre nombres en progression arithmétique ayant trois facteurs distincts.
30		Il est l'une des sommes de Kolakoski.
30! – 1 = 0,265252859… 10^33 = 265 2528598121 9105863630 8479999999		Générateur de nombre premier factoriel.
30 = 5		Factorielle oscillante de 5, symbolisée par ce symbole en S. Se reporter au lien pour sa définition.
F30 = 832 040 = 2^3 x 5 x 11 x 31 x 61 F32 = 2 178 309 et 2+1+7+8+3+0+9 = 30		Trentième nombres de Fibonacci. Le plus grand à six chiffres. Le plus petit étant: 121 393. La somme des chiffres du 32^e nombre de Fibonacci est égale à 30. Il est le seul pour 30.
B4 = B8 = – 1/30		Dénominateur du quatrième et du huitième nombre de Bernoulli.
30	Représentation du groupe de Lie E8 avec une figure à 30 sommets: Nombres du groupe Coxeter et invariance fondamentale de E8.
30 équations du 3^e degré		Posées par Fior à Tartaglia.
30 arêtes		Du dodécaèdre et de l'icosaèdre.
30 = 3x9 + 3 et ?		Énigme ultra-classique de l'hôtel à 30 euros (3 x 10) et du fameux euro manquant. Explications >>>
30 = somme magique		Carré magique particulier d'ordre 4.
30 coudées		De circonférence pour un bassin destiné au temple de Salomon – Calcul de Pi.

30 = A_Trg (5, 12, 13) = 5 x 12 / 2

30 = 5 + 12 + 13

Aire d'un triangle héronien.

Également le périmètre.

Deux triangles rectangles seulement ont leur surface (aire) égale à leur périmètre:

	Triangle 1	Triangle 3
Côtés	5 - 12 - 13	6 - 8 - 10
Pythagore	5² + 12² = 13²	6² + 8² = 10²
Périmètre	5 + 12 + 13 = 30	6 + 8 + 10 = 24
Aire	(5 x 12) / 2 = 30	(6 x 8) / 2 = 24

LA QUESTION QUI TUE

Si tu réponds correctement aux trois questions, tu seras sauvé !

Combien y a-t-il de chargements de sable sur la côte ?

Un seul à condition d'avoir un chariot assez grand.

Combien je vaux, demande le bourreau ?

39 pièces d'argent. Car Jésus a été vendu pour 30, et tu ne le vaux pas tout à fait.

Combien il y a d'étoiles dans le ciel ?

9 999, répondit l'homme.

Comment tu sais ça ?

Si tu ne me crois pas, monte là-haut et compte-les.

Voir Pensées & humour

Jeu du 30
Cette énigme a fait le tour du Net. La solution n'est pas facile. On a par exemple: 3! + 11 + 13 = 30 13,3 + 15,7 + 1 = 30 11,3135 + 9,3115 + 9.375 Avec une astuce, on a une autre solution: prendre le 9 et le retourner en 6 et faire: 6 + 11 + 13 = 30 Cette astuce est plus naturelle lorsque qu'on présente des balles portant les chiffres.	Pourquoi, pas facile? Nous ne disposons que de nombres impairs; or, la somme de trois nombres impairs est impaire et non paire comme le nombre 30 à trouver. Au moins, l'un des nombres doit être transformé en nombre pair. C'est le cas avec factorielle 3 qui s'écrit (3!) et vaut 1 x 2 x 3 = 6. Une autre astuce consiste à avoir recours aux nombres décimaux.
30 = 33 – 3 = 3^3 + 3 = 6 x 6 – 6	Faire 30 avec trois chiffres.

Voir Jeux avec chiffres sous contraintes

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 1, 1, 0] 3, [1, 0, 1, 0] 4, [1, 3, 2] 5, [1, 1, 0] 6, [5, 0] 7, [4, 2] 8, [3, 6]	9, [3, 3] 10, [3, 0] 11, [2, 8] 13, [2, 6] 13, [2, 4] 14, [2, 2]	15, [2, 0] 16, [1, 14] 17, [1, 13] 18, [1, 12] 19, [1, 11] 30, [1, 10]	9, [3, 3] 14, [2, 2] 39, [1, 1]

Voir Bases / Brésiliens

Cette page fut polluée par un remplacement malencontreux de 2 par 3. J'espère avoir tout corrigé!

Merci à Patrick De Geest pour m'avoir alerté et à avoir passer du temps à tout vérifier.

Retour	Nombre 30 – Aspects culturel
Suite	Voir le menu en haut de page
Voir	Primorielle Cristaux Palindrome retard
Site	Nombre 30 – Wikipédia Number Thirty (30) – Gary William Croft - the most comprehensive review of the number 30 ever created Tous les sites de nombres – Propriétés fondamentales
Cette page	http://villemin.gerard.free.fr/NombDico/Nb30a50/Nb30Nb.htm