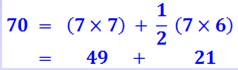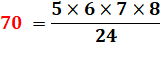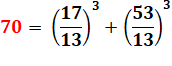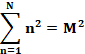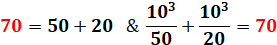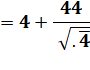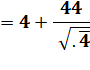soixante-dix

Édition du: 27/03/2024

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10⁶ / 10⁹ / 10¹⁰⁰ / Infini
	-0-	10		20	30		40	50	60	70	80	90
	70	71		72	73		74	75	76	77	78	79

Nombre 70

Maths 70

Culture 70

Numération 70 à 79

Soixante-dix

Septante

Seventy

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	100 0110
Bases	77₉ 55₁₃
Romain	LXX

Suite

Caractérisation du nombre

Abondant (14^e)

Abondant primitif

Admirable

Balancé

Composé

Composé inévitable (ou minimal)

Congruent

Étrange (n° 1)

Glissant

Harshad

Heureux

Idonéal

Pair

Pascal

Pascal central

Pell

Simple

Sphénique

Zumkeller

Pentagonal (7^e)

Pyramidal octogone (4^e)

13-gonal

23 – gonal centré

Pentatope

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Bible – Psaume 90:10

Les jours de nos années s'élèvent à soixante-dix ans, Et, pour les plus robustes, à quatre-vingts ans; Et l'orgueil qu'ils en tirent n'est que peine et misère, Car il passe vite, et nous nous envolons.

The days of our years are threescore years and ten; and if by reason of strength they be fourscore years, yet is their strength labour and sorrow; for it is soon cut off, and we fly away.

Voir Score = Vingt / Bible

Amusement d'enfants avec 70

Propriétés MATHÉMATIQUES

Sorte de nombre

trapèze ou pentagone

Voir Trapèze en géométrie

Géométrie

70°: construction de cet angle par neusis (compas et règle marquée).

>>>

Chiffres et numération

70 / (7+0) = 10

Divisible par la somme de ses chiffres. Nombre de Harshad.

70 = 3,5 x 20

(halvfjerdsindstyve
ou halvfjerds)

Numération danoise en base 20, où 70 se dit: "quatrième moitié" de vingt, abrégé en moitié de quatre. Les moitiés étant: 0,5 / 1,5 / 2,5 / 3,5 / 4,5.

Addition et soustraction

70 = 7 + 8 + … + 13	Une des trois sommes de nombres consécutifs >>>
70 = 7 + 8 + … + 13 = 14 x 5 = 12 + 13 + … + 16 = (17 + 18) x 2	Somme de consécutifs, égale à un multiple du nombre suivant ou de la somme des deux suivants.
70 = 3+67 = 11+59 = 17+53 = 23 +47 = 29+41	Toutes les partitions en somme de deux premiers.
0, 1, 2, 5, 12, 29, 70	Nombre de Pell.
70 = 29 + 41 70 = 23 + 47 70 = 17 + 53 70 = 11 + 59 70 = 3 + 67 70 = 2 + 3 + 5 + 11 + 13 + 17+ 19 70 = 2 + 3 + 5 + 7 + 13 + 17 + 23 70 = 2 + 3 + 5 + 7 + 11 + 19+ 23 70 = 2 + 3 + 5 + 7 + 11 + 13 + 29		57 partitions de 70 en sommes de premiers distincts, donc les 5 à deux termes et 4 à sept termes.
70 = 1x2 + 2x3 + 3x4 + 4x5 + 5x6		Somme des nombres oblongs.
70 = 1.2² + 2.3² + 3.4²		Somme de produits de nombres consécutifs.

Multiplication, division, diviseurs

70 = 2 x 5 x 7	Nombre simple. Nombre composé. Produit de trois nombres premiers distincts. Nombre sphénique n° 4. Nombre dont le plus grand facteur est égal à la somme de ses chiffres.
	Le produit de quatre nombres consécutifs est divisible par 24. Tous ces nombres figurent dans la cinquième diagonale du triangle de Pascal.
70 = 7 (3 x 7 – 1) / 2 = ½ 4 (11 x 4 – 9)	Nombre pentagonal n°7. Nombre figuré d'ordre 13. Nombre pentatope.
70 = 2 x 5 x 7 2 + 5 = 7		Nombre somme-facteurs primitif. Ils sont 12 jusqu'à 10 000.
Diviseurs de 70: 1, 2 , 5 , 7 , 10 , 14 et 35 ?		Nombre étrange ou tordu. Jamais égal à une addition de ses diviseurs. Les seuls nombres étranges inférieurs à 10 000 sont: 70, 836, 4 030, 5 830, 7192, 7 912 et 9 272 Voir Types de nombre selon la somme de leurs diviseurs
70 => {3, 9, 11, 13, 17, 19 …}		Les copremiers de 70.
= 1 + 2 + 5 + 7 + 10 + 14 + 35 + 70		La somme des diviseurs est un carré. Le Quatrième (hors 1).

70 = 8! / 4! ²

= 8! / 24² = 40 320 / 576

= 9! / 72² = 362 880 / 5 184

Factorielles divisées.

Plus petit doublet de cette forme.

70 = (4 + 4)! / (4! x 4!)

Division de factorielles.

70 = 8

Factorielle oscillante de 8.

Avec les puissances

70 = 3² + 5² + 6²

= 1² + 1² + 2² + 8²

= 1² + 2² + 4² + 7²

= 2² + 4² + 5² + 5²

= 3² + 3² + 4² + 6²

Toutes les sommes de carrés jusqu'à quatre termes.

Somme de deux cubes rationnels.

70 = 2³ + 2³ + 3³ + 3³

= 6.1³ + 4³ = 3.1³ + 5.2³ + 3³

Toutes les sommes de cubes jusqu'à neuf termes.

En puissance

70² = 1² + 2² + 3² + … + 24²

= 4 900

Seule solution (non triviale) pour que la somme des carrés consécutifs soit égale à un carré. Trouvée par Lucas.

Nombre pyramidal à base carrée.

Empilage de sphères le plus dense en dimension 24.

70² = 42² + 56² = 74² – 24²

= 182² – 168² = 250² – 240²

Triplets de Pythagore.

70³ = 15³ + 16³ + … + 34³ = 343 000

Cube somme de cubes consécutifs.

Exemple de formulation du calcul: addition des cubes de n de n = 15 à n = 34; puis, racine cubique (root (%, 3) de ce résultat (%).

Voir Table des cubes somme de cubes

2⁷⁰ = 1,18… 10²¹

= 1 180 591 620 717 411 303 424

& 424 303 114 717 026 195 081 1

Puissance de 2.

Son retourné est premier.

La somme de ses chiffres donne 70.
Seul inférieur: 2⁵ = 32 et 3 + 2 = 5.

Autour du nombre

52¹⁰ = 144555105949057024 => 1+4+4+…+4 = 70

70¹³ = 968890104070000000000000 => 9+6+8+…+0 = 52

Motif en couple.

Décimales

Racines carrées de factorielles.

Jeux, combinatoire et curiosités

	Coefficient du binôme ou nombre de Pascal. Quantité de combinaisons de 4 parmi 8.
1, 8, 28, 56, 70, 56, 28, 8, 1	Coefficient central de la ligne 8 du triangle de Pascal.
			Nombre glissant. Son primitif est 7 = 5 + 2.
		Jeu du quatre 4. Plusieurs possibilités. Avec .4 = 0, 4 = 2/5 Et .4 surligné = 0,444… = 4/9