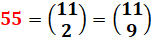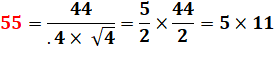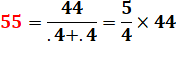Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 03/05/2025 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	50	51		52	53		54	55	56	57	58	59

Nombre 55

Maths 55

Culture 55

Numération 50 à 59

Cinquante-cinq

Fifty-five

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	11 0111
Bases	3134 = 1316
Romain	L V

Suite

Nombre réversible: Strobogrammatique

Caractérisation du nombre

Composé

Composé inévitable (ou minimal)

Congruent

Coster

Déficient

Dihédral

Fibonacci (10^e)

Impair

Kaprekar

Palin10 (5 + 5 = 10)

Palindrome

Pascal

Repdigit

Semi-premier

Simple

Stirling 1

Triangulaire (10^e)

Plus petit nombre quatre fois polygonal

18 – gonal centré

Heptagonal (5^e)

Ennéagonal centré (4^e)

Pyramidal carré (5^e)

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Nombres géométriques

Allô c'est bien de 55 55 55 55 55 ?

Oui c'est bien le 55 55 55 55 55. Que puis-je faire pour vous?

Appeler le 18 pour moi, s'il vous plait, j'ai le doigt coincé dans le cadran du téléphone.

Voir Pensées & humour / Téléphone

CARTE D'IDENTITÉ
Nombre	Composé	Département	Meuse
Facteurs	55 = 5 x 11	Élément	Césium Ca
Propriétés Typiques	55 = 1 + 2 + 3 + … + 10 = 1² + 2² + 3² + 4² + 5²	Mnémo	LOLO
	Suite Maths		Suite Culture

Propriétés CULTURELLES

Cinquante-cinq

Cinquante-cinquième

Cinquante-cinquièmement

Voir Orthographe des nombres

Espagnol Italien	Anglais Allemand
Cincuenta y cinco Cinquantacinque	fifty-five fünfundfünfzig

Voir Numération 50 à 59

Nombres et langues

Social	55 ans de mariage: noces d'émeraude. Emerald wedding anniversary.	>>>
Jeux	55 dominos au jeu du double-neuf.	>>>
Jeu	55 s'affiche sur les calculettes avec autant de barrettes que l'indique la somme de ses chiffres.	>>>
Transport	55 km plus long pont autoroutier du monde. Inauguré en octobre 2018 en Chine.	>>>
Ésotérisme	55 = 23 + 32 Tétrakis, modèle de composition de certains textes de la Bible	>>>
Chimie	55,6 moles dans un litre d'eau.	>>>

Propriétés MATHÉMATIQUES

Chiffres et numération

55 – (5 + 5) = 45 = T9		Devient triangulaire en lui retirant ses chiffres.
55	À la fois dixième triangulaire et dixième Fibonacci.

Addition et soustraction

55 = 1 + 2 + 3 + … + 10 = 1/2 10 x 11 55 = 9 + 10 + 11 + 12 + 13		Triangulaire – 10^e. Propriété objet de l'énigme des chapeaux. La somme des entiers jusqu'à 10 est un repdigit. Le plus petit exemple parmi trois connus. Somme de cinq nombres consécutifs.
55 = T10 = T2 + T3 +…+ T6		Triangulaire, somme de nombres triangulaires.
55 = 1² + 2² + 3² + 4² + 5²		Somme de cinq nombres successifs portés à une puissance. Toutes ces sommes sont divisibles par 5, sauf pour les puissances en multiple de 4.
55 = 3 + 6 + 10 + 15 + 21		Somme de nombres triangulaires (du 2^e au 6^e).
55 = 21 + 34 = F10	Fibonacci – 10^e. Le plus grand Fibonacci, concaténation de deux Fibonacci. Le seul Fibonacci en tant que repdigit. Plus grand Fibonacci triangulaire. Le plus petit Fibonacci non trivial dont la racine numérique (5 + 5 = 10) est égale à son rang.
55 = 50 + 05 = 23 + 32		Nombre sommes de retournés. Propriété générale des repdigits à deux chiffres.

Multiplication, division, diviseurs

55 = 5 x 11	Nombre composé. Nombre simple. Repdigit. Palindrome.
54 = 2 × 3^3 55 56 = 2^3 × 7	Nombre dont ses deux voisins sont divisibles par un cube: Liste (en rouge, les nombre premiers): 55, 161, 249, 271, 377, 487, 593, 687, 703, 751, 809, 919, … Voir Nombre 271 (premier)
1+1+2+3+5+8+13+21+34+55+ 89+144+233+377+610+987+ 1597+2584+4181+6765 = 17 710 = 55 x 322		La somme de 20 nombres de Fibonacci consécutif est divisible par 55.
55 divisible par 5 54 divisible par 3 56 divisible par 4		Seul nombre inférieur à 100 avec cette propriété:
			Égalité pour trois nombres voisins du produit du totient et de la somme des diviseurs.

Avec les puissances

55 = 1² + 1² + 2² + 7² = 1² + 2² + 5² + 5² = 1² + 3² + 3² + 6²	Seules sommes de carrés de deux à quatre termes.
55 = 1² + 2² + 3² + 4² + 5² = 5 x 11	Somme des 5 premiers carrés. Seule somme de cinq termes. Toujours divisible par 5 Une des cinq sommes de carrés de nombres consécutifs à être repdigit. Voir Autour de 12345
55 = 2^0 + 2^1 + 2^2 + 2^3 + 3^0 + 3^1 + 3^2 + 3^3	Motif avec somme de puissances.
55 = 10^2 – 9^2 + 8^2 – 7^2 + 6^2 – 5^2 + 4^2 – 3^2 + 2^2 – 1^2	Motif dont toutes les puissances paires sont divisibles par 11.
55 = 5 x 6 x 11 / 6	Pyramidal – 5^e.
55 = 28² – 27² = 28 + 27 = 8² – 3²	Motif général pour tout nombre impair. Différences de carrés. Début d'une suite pour les Repdigits.
55 = 3^3 + 3^3 + 1^3 = 4^3 – 2^3 – 1^3 = 10^3 – 9^3 – 6^3	Somme de cubes.
	Le produit de quatre nombres consécutifs plus 1 est un carré.

En puissance

55² = 44² + 33²		Triplet de Pythagore sur le modèle 5² = 4² + 3², chaque chiffre étant répété.
55² = 6 × 7 × 8 × 9 + 1 = 3 025		Produit de quatre nombres consécutifs plus 1 (toujours un carré)
55² = 30 25 et 30 + 25 = 55		Nombre de Kaprekar.
55^3 = 166 375 = 67 199 + 99 176 = 68 189 + 98 186 = 69 179 + 97 196 = 77 198 + 89 177 = 78 188 + 88 187 = 79 178 + 87 197	= 87 197 + 79 178 = 88 187 + 78 188 = 89 177 + 77 198 = 97 196 + 69 179 = 98 186 + 68 189 = 99 176 + 67 199			Cube avec nombres ajoutés à leur retourné.
55^7 = 1522435234375 => 1+5+2+…+5 = 46 46^7 = 435817657216 => 4+3+5+…+6 = 55			Motif en couple.

Propriété des trois derniers chiffres des puissances de 55

Identiques pour les puissances de même unité après k=1 et k=2.

Alternance entre 375 et 625 pour les puissances successives.

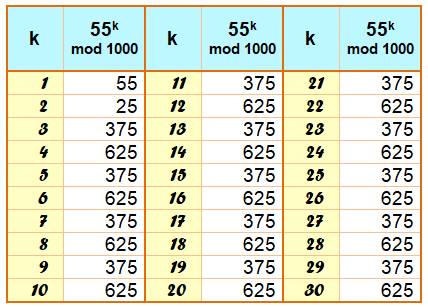
Voir Cas de 25 / Cas de 51 / Cas général des nombres en 5

Jeux et curiosités

	Coefficient du binôme ou nombre de Pascal. Quantité de combinaisons de 2 ou 9 parmi 11.
	Jeu du quatre 4. Avec la notation anglaise: .4 = 0,4 = 2/5
55 5^3 + 5^3 = 250 2^3 + 5^3 + 0^3 = 133 1^3 + 3^3 + 3^3 = 55	Invariant cubique. La somme récurrente du cube des chiffres aboutit au nombre initial.
5^3 + 5^3 = 250 2^3 + 5^3 + 0^3 = 133 1^3 + 3^3 + 3^3 = 55	Triplet narcissique. Le cycle narcissique du 13 se termine par ce cycle.

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 0, 1, 1, 1] 3, [2, 0, 0, 1] 4, [3, 1, 3] 3134 = 1316 5, [2, 1, 0] 6, [1, 3, 1] 7, [1, 0, 6] 8, [6, 7] 9, [6, 1] 10, [5, 5] 11, [5, 0]	12, [4, 7] 13, [4, 3] 14, [3, 13] 15, [3, 10] 16, [3, 7] 17, [3, 4] 18, [3, 1] 19, [2, 17] 20, [2, 15] 21, [2, 13]	22, [2, 11] 23, [2, 9] 24, [2, 7] 25, [2, 5] 26, [2, 3] 27, [2, 1] 28, [1, 27] 29, [1, 26] 30, [1, 25]	10, [5, 5] 54, [1, 1]

Voir Bases / Brésiliens

Suite	Voir le menu en haut de page Nombre 56 DicoNombre
Voir	Abaque Romain Code Gray Croissance Logistique Échec Multiplications Védiques Produit Palindrome Satellites
Cette page	http://villemin.gerard.free.fr/NombDico/Nb50a100/Nb55.htm