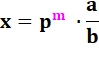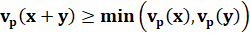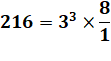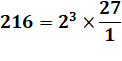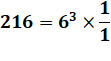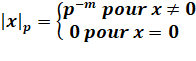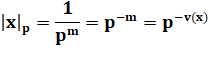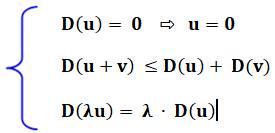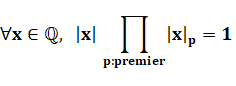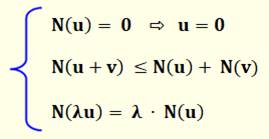|
Édition du: 19/03/2025 |
Faites un double-clic pour un retour en haut de page
![]()
|
NOMBRES p-adiques Théorie Les deux
pages précédentes nous ont familiarisés avec les étranges
nombre p-adiques. Cette nouvelle page présente la manière de les construire
et de les comparer. Sans
pouvoir aller très loin sur l'aspect théorique, on terminera par un bref tour
d'horizon des applications modernes. |
||
|
|
Sommaire de cette page >>> Les approches des p-adiques >>> Nombres p-adiques et équations >>> Valuation >>> Norme et distance >>> Propriétés et intérêt des p-adiques >>> Développements modernes >>> Annexe – Choix d'une métrique |
Débutants Glossaire |
|
Forme des nombre p-adiques On a introduit les nombres p-adiques par leur
représentation: des nombres gauchers. Ex: …123,56
(contraire des nombres réels) |
Solution des équations Parmi divers intérêts des nombres p-adiques, l'étude des racines des équations. Une solution en p-adique (plus simple à trouver)
implique une solution en réel. |
|
|
Il existe deux
approches théoriques des nombres p-adiques |
||
|
Par la NORME Il s'agit de comparer les nombres p-adiques entre
eux. Notion de distance propre à ces nombres. L'idée est simple: plus les chiffres de droite
sont communs plus les deux nombres sont proches. Ex. …999912 et …112
sont proches. Comment formaliser cela ? En introduisant une mesure (ou norme ou valution)
p-adique. La distance qui en résultera sera tout à fait
spécifique (dite ultra-métrique). SUITE >>> |
Par les SÉRIES C'est l'approche historique de Hensel. Quelle est la valeur limite d'une série (somme
infinie) de nombres ? Une notion de convergence non-conventionnelle
sera définie. En effet, dans le monde p-adique, p premier, on
souhaite trouver une suite qui tende vers 0 quand n tend vers l'infini. SUITE >>> |
|
|
Résolution des équations, relations
entre racines En 1832, Évariste Galois
montre qu'il est impossible de résoudre des équations
supérieures au quatrième degré. En revanche, il est possible
de caractériser les relations entres les
racines et de mettre en évidence leurs symétries. Par exemple x² – 2 =
0 a deux racines symétriques: |
Exemple avec une
équation du second degré dont
les racines sont r et s: À comparer à: La constante c vaut le
produit des racines et b, le coefficient de x, l'opposé de la somme (signe
moins). |
|||
|
Les nombres p-adiques sont
d'une grande utilité pour analyser les solutions des équations polynomiales:
si la solution existe en p-adique, elle existe en réel. |
Théorème de Hasse (vers 1920) Une forme
quadratique a une racine rationnelle si et seulement si elle a une solution
dans le corps des nombres p-adiques pour
tout nombre premier p ainsi qu'une solution réelle. Voir Historique |
|||
|
Pour aller plus loin, il est nécessaire de
caractériser les nombres p-adiques, les mesurer, les comparer. C'est l'objet de la norme qui permettra de
calculer une distance p-adique. |
Notions de:
|
|||
Une manière de voir
|
Quantité de zéros en base 10, un nombre se
développe comme ceci: 123 000 = 1 × 105 + 2 × 104 + 3 × 103 + 0 × 102 + 0 × 101 + 0 × 100 En factorisant: 123 000 = (1 × 102 + 2 × 10 + 3) 103 Le nombre est divisible pat 103; divisé par 104
il resterait 3. Cette puissance 3 de 10 est la plus grande puissance de 10 divisant
notre nombre. Facile ! Alors, voyons en
base 3. 1220003 = 1 × 35 + 2 × 34 + 2 × 33 + 0 × 32 + 0 × 31 + 0 × 30 Le nombre est divisible par 33;
divisé par 34 il resterait 2. Cette puissance 3 de 3 est la plus grande puissance de 3 divisant
notre nombre. Cette puissance qui représente la quantité (m) de zéros à la fin
du nombre, joue un rôle majeur pour caractériser les nombres p-adiques.
Voyons cela. Exemple: la taille des nombres en 5-adique 50 = 2 ×
5 × 5 => avec deux "5", sa taille est 1/5² = 1/25 75 = 3 ×
5 × 5 => avec deux "5", sa taille est 1/5² = 1/25 250 = 2 ×
5 × 5 × 5 => avec trois "5", sa taille est 1/53 =
1/125 1/75 =
1/3 × 1/5 x 1/5 => avec deux "5" en dénominateur, sa taille est
5² = 25. |
|
Définition
de la valuation Tout
nombre p-adique de ℚp s'écrit: Avec: C'est, en fait, la quantité de zéros à droite. |
|
Exemples 2510 = 1005 5010 = 2005 7510 = 3005 m5 = 2 x = 1,732 = 1732 10-3 |
|
|
Propriété
de la valuation La
valuation, ainsi définie, possède ces trois propriétés, du type de celles
d'une norme. |
|
||
Exemples avec le
nombre 600
|
x = 600 |
x = 600 |
x = 600 |
x = 600 |
x = 600 |
|
p = 10 |
p = 5 |
p = 4 |
p = 3 |
p = 2 |
|
x = 60010 |
x = 44005 |
x = 211204 |
x = 2110203 |
x = 10010110002 |
|
|
|
|
|
|
|
m10 = 2 |
m5 = 2 |
m4 = 1 |
m3 = 1 |
m2 = 3 |
Voir Bases
de numération
Propriétés**

Un autre exemple avec le nombre 216
|
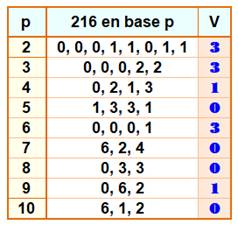
Divisibilité en base p La quantité de zéro à droite en notation normale ou
à gauche en notation informatique indique le degré de divisibilité par la
base p. Valuation V de 216 selon la
base de numération
|
21610 = 220003 =[0,0,0,2,2]3
Le nombre 26 est divisible par 33 = 27, le
quotient est 8.
La puissance 3 est la valuation de 216 en base 3. 21610 = 110110002
=[0,0,0,1,1,0,1,1]2 Le nombre 26 est divisible par 23 = 8, le
quotient est 27.
La puissance 3 est la valuation de 216 en base 2. 21610 = 10006
=[0,0,0,1]6 Le nombre 26 est divisible par 63 = 216,
le quotient est 1.
La puissance 3 est la valuation de 216 en base 6. |
|
La norme p-adique est définie par: |
|
||
|
En bref, c'est l'inverse
de p puissance m: |
|
||
|
Plus grande est la puissance de p qui divise x plus
petite est sa norme p-adique. |
|
||
|
La distance résultant de la différence de normes
est ultramétrique. Elle ne prend que des valeurs discrètes, de la
forme p-n, avec n entier relatif. Bizarre! La topologie induite est telle que tous
les triangles sont isocèles, et que tout point d'une boule est son centre. |
|
||
|
La distance classique entre nombres est métrique:
la distance entre 2 et 10 est égale à la somme des distances de 2 à 5 et de 5
à 10. Elle est comptée sur la droite des nombres. La distance p-adique est ultramétrique. Elle
obéit aux relations indiquées à droite, dont l'inégalité
triangulaire. |
|
||
|
Un p-adique est rationnel si et seulement si ses
chiffres à gauche se répètent. Pour tout entier naturel, le développement
2-adique est simplement le développement en base 2. Deux nombres ordinaires sont l'un plus grand ou égal à l'autre. Un tel ordre n'existe pas en p-adique. Avec p premier, les p-adiques forment un espace
métrique complet qui contient les
nombres rationnels comme sous-ensemble. L'ensemble des nombres p-adiques (p premier) est
stable par addition, soustraction, multiplication et division. C'est un
corps. Chaque nombre premier engendre
son propre corps de nombres p-adiques. Il contient des nombres nouveaux qui ne sont ni
réels ni complexes. Mais certains réels comme e, base
de l'exponentielle, n'est p-adique pour aucune valeur de p. Cet ensemble n'est pas démontrable. Preuve avec
une méthode du type de la diagonale de
Cantor. Avec la série géométrique
1 + a + a2 + a3 + … = 1 /(1 – a) valable pour a compris
entre -1 et 1, Euler affirme que 1 + 2 + 4 + 8 + … = 1 / (12 ) = -1. Si ce
calcul n'a pas de sens avec les nombres ordinaires, il est tout à fait recevable en dyadiques
p = 2. Généralisé avec les suites géométriques p-adiques convergentes. Dans le monde p-adique, tous les triangles sont
isocèles et deux balles sont disjointes soit l'une contient l'autre. |
|
|
Résolution d'équations en utilisant le lemme de Hensel |
Si un polynôme possède une racine simple en
p-adique, il en possède une en nombres ordinaires. |
|
En 1916, Alexander Markovitch Ostrowski démontre: Résultat fondamental de la théorie algébrique des
nombres. Les nombres p-adiques sont aussi légitimes que
les nombres réels. |
Toute valeur absolue sur les nombres rationnels
est soit équivalente à la valeur absolue usuelle, soit à une valuation
p-adique. |
|
Avec la norme p-adique, on définit le corps des
p-adiques. Possibilité de réaliser les quatre opérations. |
Décomposition unique en facteurs. Leur forme canonique:
|
|
La norme de la différence constitue une métrique sur
les nombres p-adiques
|
Surprenant:
pour p = 5, le nombre 135 est plus proche de 10 que de 35. 135 = 10205 10 = 205 35 = 1205 135 – 10 = 10005 norme 10-3 135 – 35 = 4005 norme 10-2 |
|
Cette formule est utilisée pour résoudre de nombreux
problèmes en théorie des nombres. Notamment en utilisant le théorème de Hasse qui
indique, en gros, qu'une équation peut être résolue en nombres rationnels ssi
elle est résolue en réels et en p-adique pour tous les premier p. |
|
|
Lorsque les nombres p-adiques ont été introduits,
ils ont été considérés comme une partie exotique des mathématiques pures sans
aucune application. Puisque les nombres p-adiques ont la propriété
intéressante selon laquelle on dit qu'ils sont proches lorsque leur
différence est divisible par une puissance élevée de p, plus la puissance est
élevée, plus ils sont proches. Cette propriété des p-adiques permet de coder
l'information de congruence avec des applications puissantes dans la théorie
des nombres y compris, par exemple, dans la célèbre preuve du dernier
théorème de Fermat. En 1968, A. Monna et F. van des Blij proposent d'appliquer les p-adiques à la
physique. En 1972, E. Beltrametti et G. Cassinelli
cherchent à les utiliser en mécanique quantique. Notamment, les physiciens tentent de créer de
nouveaux modèles de l'espace-temps qui permettraient de décrire les distances
de Planck. Le fait que les nombres p-adiques sont sans ordre serait une
propriété intéressante. La représentation des nombres p-adiques par des
séquences de chiffres donne une possibilité d'utiliser ce système de nombres
pour le codage de l'information. Ainsi, donc les modèles p-adiques peuvent
être utilisés pour la description de nombreux processus d'information. En
particulier, ils peuvent être utilisés en sciences cognitives, en psychologie
et en sociologie. Ces modèles basés sur des systèmes dynamiques p-adiques. De plus, il existe des études en informatique et
en cryptographie qui, avec la physique mathématique ont stimulé, en 1990, des
recherches intensives sur la dynamique p-adique puisqu'il a été observé que
les principales instructions informatiques (et donc les programmes composés
de ces instructions) peuvent être considérés comme des transformations
continues par rapport à la métrique 2-adique. Programme
de Langlands: c'est notamment, une
recherche d'une manière de relier chaque groupe de Galois (relations
entre les racines d'un polynôme) avec des formes automorphiques (formes qui
se reproduisent elles-mêmes). Plus généralement, recherche de structures
internes de haut niveau entre divers objets mathématiques. Il est parfois
plus facile de démontrer une propriété dans le monde image (par
transformation automorphique) que dans le monde d'origine. |
|
![]()
|
Choix d'une
métrique** (norme) |
||
|
Normes familières On connait la valeur absolue sur les nombres
réels. Le module sur l'ensemble des complexes. On généralise la notion de norme avec cette
définition. Définition générale de la norme Une norme sur un espace vectoriel E est une
application N qui fait correspondre à chaque vecteur u de E un réel positif
N(u) vérifiant les trois propriétés indiquées, pour tous vecteurs u, v de E
et tout réel λ. |
Propriétés d'une norme
|
|
|
Convergence (limite) On dit que la suite Il s'agit ainsi d'une limite de nombres réels. Ex: 0,3;
0,33; 0,333; 0,3333; …. tend vers 1/3. |
La norme euclidienne est la plus courante: pour u
= (x, y) dans ℝ², on pose:
Notion classique de distance entre deux points. |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |